4.2: Mejora de la Respuesta Transitoria
- Page ID
- 84838
Mejora de la respuesta transitoria
Consideramos el sistema de control de retroalimentación (Figura 4.2.1) con entrada\(r(s)\) y salida\(y(s)\).
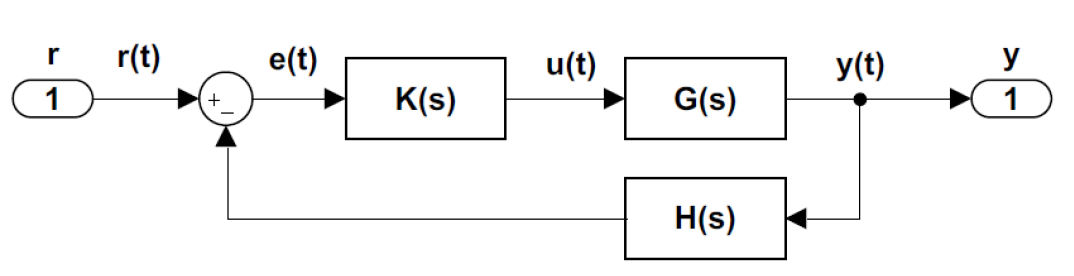
La respuesta del sistema de bucle cerrado se da como:\(y(s)=T(s)r(s)\), donde\(T(s)=\frac{KG(s)}{1+KGH(s)} \).
La respuesta del sistema consiste en componentes transitorios y de estado estacionario, es decir,\(y(t)=y_{tr}(t)+y_{ss}(t)\).
En particular, para una entrada constante,\(r_{ss}\), el componente de estado estacionario de la respuesta del sistema se da como:\(y_{ss}=T(0)r_{ss}\).
La respuesta transitoria se caracteriza por las raíces del polinomio característico de bucle cerrado, dado como:\(\Delta(s)=1+KGH(s)\).
Estas raíces pueden ser reales o complejas, distintas o repetidas. En consecuencia, los modos de respuesta natural del sistema se caracterizan de la siguiente manera:
Raíces Reales y Distintas. Dejar\(\Delta (s)=(s-p_{1} )(s-p_{2} )\ldots (s-p_{n} ).\); entonces, los modos de respuesta natural del sistema se dan como:\(\left\{e^{p_{1} t} ,e^{p_{2} t} ,\; \ldots \, ,e^{p_{n} t} \right\}\).
Raíces Reales y Repetidas. Dejar\(\Delta _{m} (s)=(s-s_{1} )^{m}\); entonces, los modos de respuesta natural correspondientes se da como:\(\left\{e^{s_{1} t} ,\; te^{s_{1} t} ,\; \ldots ,\; t^{m-1} e^{s_{1} t} \right\}\).
Raíces Complejas. Dejar\(\Delta _ c (s)=(s+\sigma )^{2} +\omega ^{2} \); entonces, los modos de respuesta natural correspondientes se dan como:\(\left\{e^{-\sigma t} \cos \omega t\; ,\; \; e^{-\sigma t} \sin \omega t\right\}\).
Expresión General. Supongamos que para un polinomio de orden\(n\) th, los modos de respuesta se dan como:\(\phi _{k} (t),\; k=1,\ldots ,n\). Entonces, utilizando constantes arbitrarias,\(c_{k}\), la respuesta natural del sistema se da como:\(y(t)=\sum _{k=1}^{n} c_{k} \phi _{k} (t)\nonumber\).
Especificaciones de diseño del sistema de control
Las especificaciones de diseño del sistema de control incluyen características deseadas para los componentes transitorios y de estado estacionario de la respuesta del sistema con respecto a una entrada prototipo. Se utiliza una entrada de paso para definir las características de respuesta transitoria deseadas.
Los indicadores cualitativos de la respuesta escalonada incluyen los siguientes:
- El tiempo de subida (\(t_{r}\))
- La hora pico (\(t_{p}\))
- El pico de respuesta (\(M_p\)) y el porcentaje de sobreimpulso (%OS),
- El tiempo de asentamiento (\(t_{s}\))
Tiempo de Subida. Para los sistemas sobreamortiguados (\(\zeta >1\)), el tiempo de subida es el tiempo que tarda la respuesta en llegar de\(10\%\) a\(90\%\) de su valor final. Para los sistemas con poca amortiguación (\(\zeta <1\)), el tiempo de subida es el momento en que la respuesta alcanza por primera vez su valor de estado estacionario.
Hora Pico. Para sistemas poco amortiguados, el tiempo pico es el momento en que la respuesta escalonada alcanza su pico.
Sobreimpulso de pico. El sobreimpulso máximo es el sobreimpulso por encima del valor de estado estacionario.
Tiempo de sedimentación. El tiempo de asentamiento es el momento en que la respuesta escalonada alcanza y permanece dentro\(2\%\) de su valor de estado estacionario. Como alternativa, se pueden usar\(1\%\) límites.
Sistema prototipo de segundo orden
Para ilustrar las características anteriores, consideramos una función prototipo de transferencia de segundo orden, dada por la función de transferencia de bucle cerrado como:\[T\left(s\right)=\frac{{\omega }^2_n}{s^2+2\zeta {\omega }_ns+{\omega }^2_n}\]
Los polos para el sistema prototipo se encuentran en:\(s=-\zeta {\omega }_n\pm j{\omega }_d\), donde\({\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}\) está la frecuencia natural amortiguada.
El impulso y la respuesta escalonada del sistema prototipo se dan como:\[y_{imp}(t)=\frac{{\omega }^2_n}{{\omega }_d} e^{-\zeta {\omega }_nt}{\sin \left({\omega }_dt\right)\ }u(t)\]
\[y_{step}(t)=T(0) \left(1-e^{-\zeta {\omega }_n t} \sin \, (\omega _{d} t+\phi)\right)\, u(t),\, \, \, \phi =\tan ^{-1} \frac{\omega_d }{\zeta\omega _n } \]
Para el sistema prototipo, el tiempo de subida,\(t_r\), está indicado por\({\omega }_dt_r+\phi =\pi\). Así,\(t_r=\frac{\pi -\phi }{{\omega }_d}\); el tiempo de subida se limita como:\(\frac{\pi }{2{\omega }_d}\le t_r\le \frac{\pi }{{\omega }_d}\).
El tiempo pico está indicado por\({\omega }_dt_p=\pi\); así,\(t_p=\frac{\pi }{{\omega }_d}\).
El sobreimpulso máximo se da como:\(M_p=1+e^{-\zeta {\omega }_nt_p}\); el porcentaje de sobreimpulso se da como:\(\%OS=100e^{-\zeta {\omega }_nt_p}\).
La constante de tiempo efectiva del sistema prototipo es:\(\tau =\frac{1}{\zeta {\omega }_n}\). La respuesta escalonada alcanza y permanece dentro\(2\%\) de su valor final en aproximadamente\(4\tau\), y dentro\(1\%\) de su valor final en aproximadamente\(4.5\tau\).
Estas métricas se resumen en la Tabla siguiente.
| Indicador de calidad | Expresión |
|---|---|
| Tiempo de subida | \(t_r=\frac{\pi -\phi }{{\omega }_d},\ \ \phi ={{tan}^{-1} \frac{\sqrt{1-{\zeta }^2}}{\zeta }\ }\) |
| Hora pico | \(t_p=\frac{\pi }{{\omega }_d}\) |
| Sobreimpulso de pico | \(M_p=100e^{-\zeta {\omega }_nt_p}(\%)\) |
| Tiempo de sedimentación | \(t_s\cong \frac{4.5}{\zeta {\omega }_n}\) |
Podemos señalar que los indicadores de calidad de respuesta escalonada anteriores son todas funciones de la relación de amortiguación\(\zeta\),, de las raíces de bucle cerrado.
Para aclarar esta relación, la variación en el sobreimpulso escalonado,\(\% { OS}\), y el tiempo de subida normalizado,\({\omega }_nt_r\), con\(\zeta\) se tabula a continuación para los valores seleccionados de\(\zeta\).
Cuadro 2.2: Porcentaje de sobreimpulso y tiempo de subida vs. relación de amortiguación
| \(\zeta\) | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 |
|---|---|---|---|---|---|
| \ (\ zeta\)” style="text-align:left;” class="lt-eng-24403">\(\% { OS}\) | 0.2% | 1.5% | 4.6% | 9.5% | 16.3% |
| \ (\ zeta\)” style="text-align:left;” class="lt-eng-24403">\({\omega }_nt_r\) | 5.54 | 4.18 | 3.3 | 2.76 | 2.42 |
A menudo se desea un sobreimpulso bajo (\(\le 10\%\)) en la respuesta escalonada, lo que se traduce en\(\zeta \ge 0.6.\)
Ejemplo\(\PageIndex{1}\)
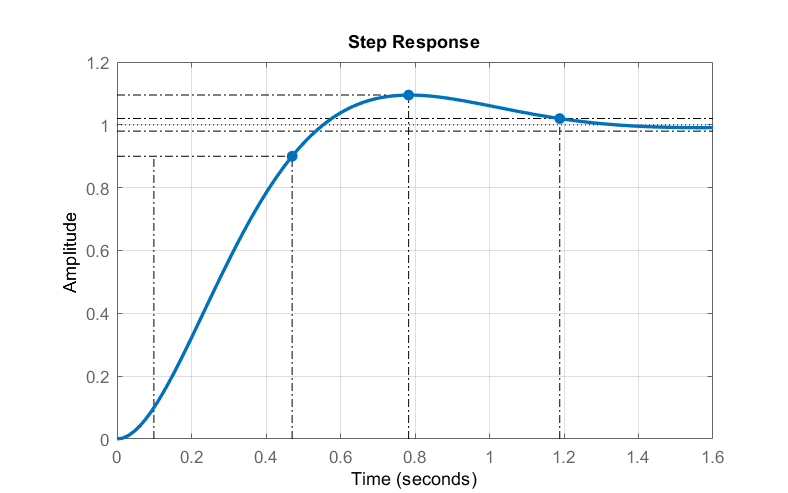
Para un prototipo de sistema de segundo orden, vamos\(T\left(s\right)=\frac{25}{s^2+6s+25}\). Los polos de bucle cerrado se encuentran en:\(p_{1,2}=-3\pm j4\), por lo tanto\({\omega }_n=5\frac{rad}{s}\) y\(\zeta =0.6\).
La respuesta escalonada del sistema muestra:\(t_r\cong 0.47\,sec, \;t_p\cong 0.78\,sec, \;\%OS=9\%\), y\(t_s\cong 1.19\,sec \) (\(2\%\)umbral).
Polinomio característico de bucle cerrado deseado
Las especificaciones de diseño del sistema, expresadas en términos de tiempo de subida (\(t_r\)), tiempo de asentamiento (\(t_ s\)), relación de amortiguación (\(\zeta\)) y porcentaje de sobreimpulso (\(\% { O}S\)), se utilizan para definir las ubicaciones de raíz deseadas para el polinomio característico de bucle cerrado.
En particular, asumiendo una ubicación raíz\(-\sigma \pm j\omega\), se colocan las siguientes restricciones en las partes real e imaginaria:
- La restricción de tiempo de asentamiento coloca un límite en la parte real de las raíces:\(\sigma \ge \frac{4.5}{t_s}\).
- La restricción de relación de amortiguación requiere que:\(\theta \le \pm \cos ^{-{ 1}} \zeta\), donde\(\theta\) está el ángulo de la ubicación de raíz deseada desde el origen del plano complejo.
- La restricción de tiempo ascendente coloca un límite en la frecuencia natural de las raíces de bucle cerrado como\({\omega }_n\ge \frac{2}{t_r}\).
Estas restricciones se resumen a continuación:
\[\sigma \ge \frac{4.5}{t_s},\ \ {\omega }_n\ge \frac{2}{t_r},\ \ \theta \le\cos^{-1} \zeta \]
Ejemplo\(\PageIndex{2}\)
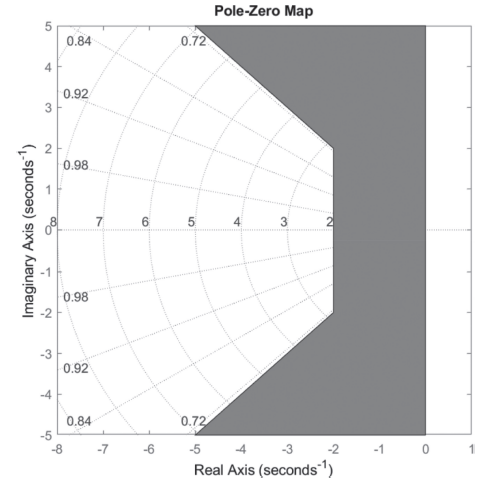
Asumimos las siguientes especificaciones de diseño:\(0.7<\zeta <1\) y\(t_{s} <2s\). Entonces, la región deseada para las ubicaciones de raíz de bucle cerrado está delimitada por:\(\sigma \ge 2\) y\(\theta \le \pm 45^{\circ }\).
Ejemplo\(\PageIndex{3}\)
Supongamos que las especificaciones de diseño se especifican como:\(t_r \le 0.5 s\)\(t_ s \le 3.0 s\),, y%\({ \% O}S\le 10\%\). Estas especificaciones imponen las siguientes restricciones en las ubicaciones de los polos de bucle cerrado:\(\sigma \ge 1.5,\ {\omega }_n\ge 4,\) y\(\zeta \ge 0.6\).
Para cumplir con las restricciones, podemos elegir, por ejemplo, el polinomio característico de bucle cerrado deseado como:\(\Delta_{des}(s)=(s+\sigma )^2+{\omega }^2_d=s^2+6s+20\).
Selección de ganancia del controlador
El polinomio característico de bucle cerrado para un sistema de retroalimentación de ganancia unitaria incluye ganancia de controlador estático\(K\),, como parámetro. El polinomio característico se da como:\(\Delta(s,K)=1+KG(s)\).
Dado un polinomio característico deseado\(\Delta_{des}(s)\), podemos elegir la ganancia del controlador comparando los coeficientes de los dos polinomios.
Ejemplo\(\PageIndex{4}\)
El modelo simplificado de un pequeño motor de CC se da como:\(G(s)=\frac{\theta (s)}{V_a (s)} =\frac{10}{s(s+6)} .\) Suponiendo un controlador de ganancia estática en configuración de retroalimentación de ganancia unitaria, el polinomio característico de bucle cerrado se da como:\(\Delta\left(s\right)=s^2+6s+10K\).
Supongamos que las especificaciones de diseño se dan como:\(OS\le 10\%\ \left(\zeta \ge 0.6\right),\ t_s\le 1.5sec.\) Entonces, las ubicaciones de raíz de bucle cerrado pueden seleccionarse como:\(s=-3\pm j4\).
El polinomio característico deseado se forma como:\(\Delta_{des}(s)=s^2+6s+25\).
Al comparar coeficientes polinomiales, obtenemos:\(K=2.5\).
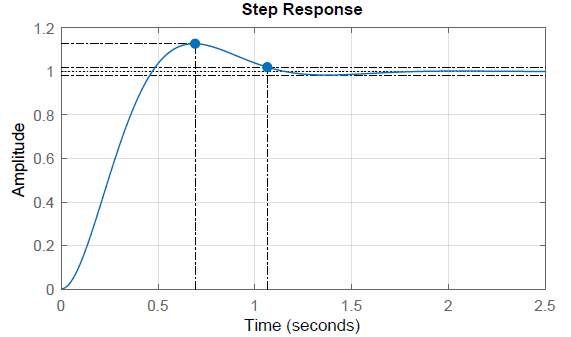
La respuesta de paso del sistema de bucle cerrado muestra un tiempo de subida\(t_r\cong 0.47\,sec\) (\({\omega }_nt_r\cong 3\)) y el tiempo de asentamiento\(t_s\cong 1.06\ sec\).
El siguiente ejemplo ilustra el diseño del controlador de retroalimentación de velocidad.
Ejemplo\(\PageIndex{5}\)
El polinomio característico para el diseño del controlador de retroalimentación de velocidad se da como:\(\Delta (s,K,K_{1} )=s^{2} +K_{1} s+K\).
Supongamos que los objetivos del diseño son:\(\% \; { O}S\le 5\% \, (\zeta =0.7)\) y\(t_ s \le 2.5s.\)
Un polinomio característico deseado para\(\zeta =0.7\) y\(\zeta \omega _{n} =2\) se da como:\(\Delta _{ des} (s)=(s+2)^{2} +2^{2}\). En consecuencia, podemos elegir:\(K_{1} =4,K=8\).
Índices de rendimiento óptimo
Una forma alternativa de caracterizar la respuesta transitoria del sistema de bucle cerrado es definir un índice de rendimiento en el dominio del tiempo y elegir un polinomio característico para minimizar ese índice.
Con este fin, se han definido tres índices de desempeño populares:
Error Absoluto Integral,\({ I}A{ E}:\; \int _{0}^{t_{s} } \left|e(t)\right| dt\)
Error Cuadrado Integral,\(\; { I}SE:\; \int _{0}^{t_{s} } \left|e(t)\right|^{2} dt\)
Error Absoluto de Tiempo Integral,\({ I}TAE:\; \int _{0}^{t_{s} } t\left|e(t)\right| dt.\)
El índice ITAE, en particular, se utiliza comúnmente para evaluar el desempeño del sistema en el control de procesos industriales.
Para un modelo prototipo de sistema de segundo orden, impulsado por una entrada escalonada, la minimización del índice ITAE da como resultado un diseño óptimo con\(\zeta =0.7\) (\(\% { O}S=4.6\%\)).
Los coeficientes óptimos de los polinomios característicos deseados basados en el índice ITAE se dan a continuación:
\[s+\omega _{n}\]
\[s^{2} +1.4\omega _{n} s+\omega _{n}^{2}\]
\[s^{3} +1.75\omega _{n} s^{2} +2.15\omega _{n}^{2} s+\omega _{n}^{3}\]
\[s^{4} +2.1\omega _{n} s^{3} +3.4\omega _{n}^{2} s^{2} +2.7\omega _{n}^{2} s+\omega _{n}^{3} .\]
Ejemplo\(\PageIndex{6}\)
El modelo de primer orden-más tiempo muerto (FOPDT) de un proceso industrial se da como:\(G\left(s\right)=\frac{e^{-s}}{s+1}\). Al utilizar la aproximación de Pade de primer orden:\(e^{-s}\cong \frac{2-s}{2+s}\), obtenemos una aproximación racional como:\(G\left(s\right)\cong \frac{2-s}{(s+1)(s+2)}\).
El polinomio característico de bucle cerrado para un sistema de control de retroalimentación de ganancia de unidad es:\(\Delta\left(s\right)=\left(s+1\right)\left(s+2\right)+K(2-s)\).
Usando el índice ITAE, se selecciona un polinomio de segundo orden deseado como:\(\Delta_{des}(s)=s^{2} +1.4\omega _{n} s+\omega _{n}^{2}\).
Al comparar los coeficientes polinomiales, obtenemos dos ecuaciones que se resuelven para obtener:\({\omega }_n=1.76\frac{rad}{s}\) y\(K=0.54\).


