4.3: Mejora de errores en estado estacionario

Error de seguimiento en estado estacionario

Un sistema de control de seguimiento está diseñado para tener un error de estado estacionario bajo en respuesta a una entrada constante (es decir, unidad-paso) o linealmente variable (es decir, rampa de unidad). La tolerancia de error deseada puede especificarse como porcentaje de la entrada de referencia. Además, la respuesta del sistema a una entrada de perturbación constante debe permanecer pequeña.

Consideramos el sistema de control de retroalimentación (Figura 4.3.1) con entrada\(r(s)\) y salida\(y(s)\).

Figura\(\PageIndex{1}\): Copiar y Pegar Subtítulo aquí. (Copyright; autor vía fuente)

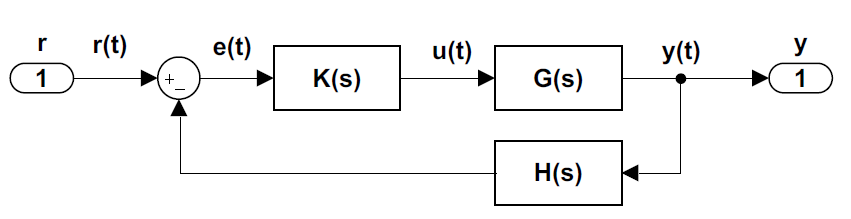
Dejar\(T\left(s\right)\) denotar la función de transferencia de bucle cerrado; entonces\(y\left(s\right)=T\left(s\right)r(s)\). El error de seguimiento\(e(s)\), en respuesta a una señal de referencia\(r(s)\), se define como:

\[e\left(s\right)=\left(1-T(s)\right)r\left(s\right)\]

Para caracterizar el error de seguimiento, consideramos un sistema de retroalimentación unidad-ganancia (\(H(s)=1\)). Entonces, el error de rastreo,\(e(s)\), se da como:

\[e(s)=\frac{1}{1+KG(s)} r(s)\]

Mediante el uso del teorema del valor final (FVT), el error de seguimiento de estado estacionario se calcula como:\(e(\infty )={\mathop{\lim }\limits_{s\to 0}} \:se(s) \)

El error de estado estacionario a una entrada de referencia de paso\(\left(r(s)=\frac{1}{s} \right)\),, se da como:\(e(\infty )=\frac{1}{1+KG(0)} .\)

El error de estado estacionario a una entrada de referencia de rampa\(\left(r(s)=\frac{1}{s^{2} } \right)\),, se da como:\(e(\infty )=\frac{1}{\left. sKG(s)\right|_{s=0} } .\)

Constantes de error del sistema

El error de seguimiento de estado estacionario en el caso de un sistema de control de retroalimentación de ganancia de unidad se caracteriza en términos de constantes de error de posición y velocidad del sistema, que se definen como:

\[K_ p ={\mathop{\lim }\limits_{s\to 0}} KG(s)\]

\[K_{ v} ={\mathop{\lim }\limits_{s\to 0}} sKG(s)\]

En términos de las constantes de error, el error de seguimiento de estado estacionario a una entrada de paso o rampa se evalúa como:

\[\left. e(\infty )\right|_{ step} =\frac{1}{1+K_ p }\]

\[\left. e(\infty )\right|_{ ramp} =\frac{1}{K_v } \]

Ejemplo\(\PageIndex{1}\)

Vamos\(KG(s)=\frac{K}{s(s+2)}\); entonces tenemos:\(K_ p =\infty ,\; \; K_{ v} =\frac{K}{2}\).

De ahí\(\left. e(\infty )\right|_{ step} =0, \;\left. e(\infty )\right|_{ramp} \; =\; \frac{2}{K} .\)

Observamos que la presencia de un integrador en el bucle obliga\(K_p\to \infty\), y el error de estado estacionario a una entrada de paso para ir a cero.

Ejemplo\(\PageIndex{2}\)

El modelo aproximado de un pequeño motor de CC se da como:

\[KG\left(s\right)=\frac{500K}{\left(s+10\right)\left(s+100\right)}\]

Entonces tenemos:\(K_p=0.5K\), y\(K_v=0\).

De ahí\(\left. e(\infty )\right|_{ step} =\frac{2}{K}, \;\left. e(\infty )\right|_{ramp} \; =\; \infty .\)

El control integral\(K\left(s\right)=\frac{k_i}{s}\), a menudo se emplea para reducir el error de seguimiento en estado estacionario. La presencia de un integrador en las fuerzas de bucle\(K_p\to \infty\), y el error de estado estacionario a una entrada de paso para ir a cero.

Error de estado estacionario a la entrada de rampa

Suponiendo que el bucle de retroalimentación contiene un integrador, de modo que el error de estado estacionario a una entrada de paso es cero, el error de estado estacionario a una entrada de rampa se expresa como:

\[e(s)=\left[1-T(s)\right]r(s);\; \, \, r(s)=\frac{1}{s^{2} } .\]

El error se evalúa mediante la aplicación de FVT:\(\left. e(\infty )\right|_{ramp} ={\mathop{\lim }\limits_{s\to 0}} \frac{1-T(s)}{s} .\)

Al usar la regla del Hospital L', obtenemos:\(\left. e(\infty )\right|_{ramp} ={\mathop{\lim }\limits_{s\to 0}} \, \left(-\frac{ dT(s)}{ ds} \right)\).

Para evaluar el RHS, utilizamos el logaritmo natural para escribir:\(\frac d{ ds} \ln T(s)=\frac{1}{T(s)} \frac{ dT(s)}{ ds} .\)

Ya que\({\mathop{\lim }\limits_{s\to 0}}\; T(s)=1\) por el supuesto integrador, tenemos:\({\mathop{\lim }\limits_{s\to 0}}\;\frac d{ ds} \ln T(s)\; ={\mathop{\lim }\limits_{s\to 0}} \;\frac{ dT(s)}{ ds}\).

A continuación, supongamos que\(T(s)\) se expresa como:\(T(s)=\frac{K(s-z_{1} )\ldots (s-z_{m} )}{(s-p_{1} )\ldots (s-p_{n} )} .\)

Entonces, tenemos:\(\ln T(s)=\ln K+\sum _{{ l}n} (s-z_{i} )-\sum _{{ l}n} (s-p_{i} ),\) y

\[\frac d{ ds} \ln T(s)=\ln K+\sum \frac{1}{s-z_{i} } -\sum \frac{1}{s-p_{i} } \]De ello se deduce que:\[\left. e(\infty )\right|_{ ramp} =\sum \frac{1}{p_{i} } -\sum \frac{1}{z_{i} } \]

donde\(z_{i}\) y\(p_{i}\) denotan los ceros y polos del sistema de bucle cerrado.

Ejemplo\(\PageIndex{3}\)

Dejar\(KG(s)=\frac{K}{s(s+2)}\); entonces, el polinomio característico de bucle cerrado es:\(\mathit{\Delta}\left(s\right)=s^2+2s+K\).

Asumiendo un valor de\(K=1\), los polos de bucle cerrado se encuentran en:\(s_{1,2}=-1,\ -1\).

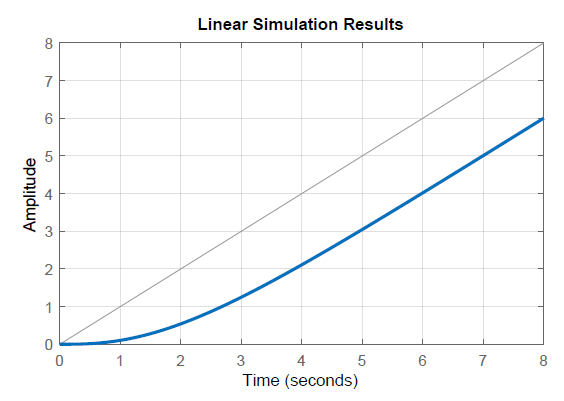
El error de estado estacionario resultante a una entrada de rampa se da como:\(\left. e(\infty )\right|_{ramp} =\sum \frac{1}{p_{i} } =2\).

Para la verificación, la respuesta del sistema de bucle cerrado se grafica en la Figura 4.3.1.

Figura\(\PageIndex{1}\): Error de estado estacionario a una entrada de rampa (Ejemplo 4.3.3).