5.1: Fundamentos del locus radicular

Locus Raíz

El locus raíz (RL) constituye un gráfico de las ubicaciones de raíz de bucle cerrado, con variación en la ganancia del controlador de retroalimentación estática,\(K\).

Para desarrollar los conceptos de RL, consideramos un sistema típico de control de retroalimentación (Figura 5.1), donde\(K\) representa un controlador,\(G(s)\) es la función de transferencia de planta, y\(H(s)\) es la función de transferencia de sensores. A menos que se indique lo contrario, se asume la retroalimentación de ganancia de unidad (\(H(s)=1\)).

Figura\(\PageIndex{1}\): Sistema de control de retroalimentación con planta\(G(s)\)\(H(s)\), sensor y un controlador de ganancia estática representado por\(K\).

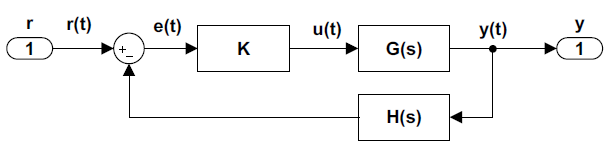
La ganancia de bucle para el bucle de retroalimentación incluye el controlador, la planta y las funciones de transferencia del sensor, y se da como:\[L(s)=KG(s)H(s)=KGH(s)\]

El polinomio característico del sistema de bucle cerrado se define como:\[\Delta (s,K)=1+KGH(s)\]

Las raíces de\(\Delta (s,K)\) varían con la ganancia del controlador,\(K\), y se trazan para diferentes valores de\(K\). Los loci de todas esas ubicaciones de raíces, como\(K\) varía de,\(0\to \infty ,\) constituye la gráfica de locus raíz de la función de transferencia de bucle.

Ejemplo\(\PageIndex{1}\)

Let\(G(s)=\frac{1}{s+1} ,\; H(s)=1\); el polinomio característico de bucle cerrado se da como:\(\Delta (s)=s+1+K.\) El polinomio tiene una sola raíz en\(s_{1} =-1-K\).

Una tabla corta de raíz de bucle cerrado para diferentes valores de\(K\) se da a continuación:

\(K\)	\(0\)	\(1\)	\(2\)	\(5\)	\(10\)
Raíz de bucle cerrado	\(-1\)	\(-2\)	\(-3\)	\(-6\)	\(-11\)

La gráfica de locus raíz, según\(K\) varía de\(0\) a\(\infty\), traza una línea que\(\sigma =-1\) avanza desde el eje real negativo hasta el infinito (Figura 5.1.2). La rejilla superpuesta muestra la relación de amortiguación de la raíz de bucle cerrado (\(\zeta=1\)en este caso).

Figura\(\PageIndex{2}\): La gráfica del locus radicular para\(G(s)=\frac{1}{s+1} ,\; H(s)=1\)

pkg load control
s=tf('s');
Gs=1/(s+1);
rlocus(Gs)

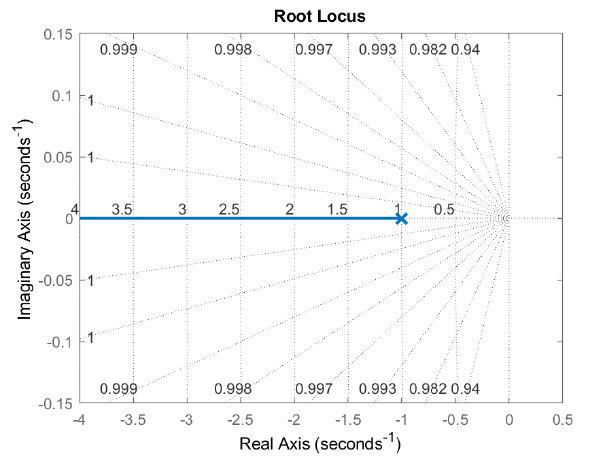
MATLAB Control Systems Toolbox proporciona el comando 'rlocus' para trazar el locus raíz de la función de transferencia de bucle. El comando 'rlocus' se invoca después de definir un objeto de sistema dinámico usando el comando 'tf' o 'zpk'.

El comando 'grid' agrega relación de amortiguación constante y contornos de frecuencia natural constante a la gráfica RL. Estos contornos ayudan a diseñar un controlador estático para los valores deseados de esos parámetros.

Ejemplo\(\PageIndex{2}\)

Vamos\(G(s)=\frac{1}{s(s+2)} ,\; \; H(s)=1\). El polinomio característico de bucle cerrado se da como:\(\Delta (s,K)=s^{2} +2s+K.\)

Las raíces del polinomio característico se dan como:\(s_{1,2}=-1\pm \sqrt{1-K}\) para\(K\le 1\), y como\(s_{1,2} =-1\pm j\sqrt{K-1}\) para\(K>1\). Las raíces para los valores seleccionados de\(K\) se tabulan a continuación.

\(K\)	\(0\)	\(1\)	\(2\)	\(10\)
Raíces de bucle cerrado	\(-1,-2\)	\(-1,-1\)	\(-1\pm j1\)	\(-1\pm j3\)

Los loci de estas raíces, como\(K\) varía de\(0\to \infty\), comprenden dos ramas que comienzan en los polos de bucle abierto (OL) ubicados en\(\{ 0,\; -2\}\), avanzan hacia adentro a lo largo del eje real para encontrarse en\(\sigma =-1\), luego se dividen y se extienden a lo largo de la\(\sigma =-1\) línea hasta\(s=-1\pm j\infty\) (Figura 5.2). Estas direcciones se llaman asíntotas RL.

Figura\(\PageIndex{3}\): La gráfica del locus radicular para\(G(s)=\frac{1}{s(s+2)} ,\; \; H(s)=1\).

pkg load control
s=tf('s');
Gs=1/s/(s+1);
rlocus(Gs)

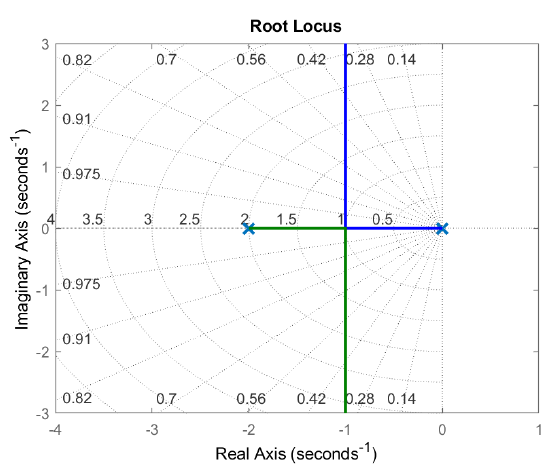
La gráfica RL se puede extender a valores negativos de\(K\), i.e.\(K\in (-\infty ,\; \infty )\), y se denomina locus radicular generalizado.

Reglas de locus raíz

Todas las parcelas RL comparten algunas propiedades comunes, denominadas reglas de locus raíz. A continuación se describen las reglas destacadas.

A continuación, se supone que la función de transferencia de bucle,\(KGH(s)\), es apropiada, tiene polos de bucle\(n\) abierto (OL) y ceros OL\(m\le n\) finitos. Se supone que los\(n-m\) ceros restantes se encuentran en el infinito.

1. El RL tiene\(n\) ramas y\(n-m\) asíntotas (asumió direcciones RL para grandes\(K\)). Las ramas RL comienzan en los polos OL (for\(K=0\)); de estas, las\(m\) ramas terminan en los ceros OL (as\(K\to \infty\)); las\(n-m\) ramas restantes siguen a las asíntotas RL hasta el infinito (as\(K\to \infty\)).
2. El locus del eje real, que indica raíces reales del polinomio característico, se encuentra a la izquierda de un número impar de polos y ceros de\(KGH(s)\) for\(\left(K>0\right)\), y a la derecha de un número impar de polos y ceros para\(\left(K<0\right)\).
3. El locus del eje real que separa un par de polos OL contiene un punto de ruptura donde las dos ramas RL se dividen; el locus del eje real que separa dos ceros OL, contiene un punto de ruptura donde las dos ramas se encuentran. Los puntos de ruptura para ambos\(K>0\) y\(K<0\) se encuentran entre las soluciones a la ecuación:\(\sum \frac{1}{\sigma -p_{i} } -\sum \frac{1}{\sigma -z_{i} } =0\).
4. Las asíntotas RL, asumen ángulos:\(\phi _{a} =\frac{2k+1}{n-m} (180^{\circ } ),\; k=0,\; 1,\cdots ,n-m-1\), (para\(K>0\)), y ángulos:\(\phi _{a} =\frac{2k+1}{n-m} (360^{\circ })\),\(k=0,\; 1,\cdots ,n-m-1\) (para\(K<0\)). Estas asíntotas se cruzan en un punto común en el eje real, dado como:\(\sigma _a =\frac{\sum p_{i} -\sum z_{i} }{n-m}\).
5. La gráfica RL es simétrica con respecto al eje real (esto es consecuencia de que las raíces complejas de un polinomio real ocurren en pares conjugados).

Las reglas anteriores bastan para esbozar la parcela RL para plantas de bajo orden. Se pueden agregar reglas adicionales para refinar la parcela RL.

Ejemplo\(\PageIndex{3}\)

Let\(KGH(s)=\frac{K(s+3)}{s(s+2)}\); por lo tanto,\(n=2,\ \ m=1\) .El polinomio característico de bucle cerrado se forma como:\(\mathit{\Delta}\left(s,K\right)=s^2+\left(K+2\right)s+3K\).

La gráfica RL se esboza de la siguiente manera:

1. El RL tiene dos ramas que comienzan en los polos OL en\(0,-2\) (para\(K=0)\); una rama termina en el OL finito cero en\(s=-3\); la otra rama sigue a la asíntota RL como\(K\to \infty\).
2. El locus del eje real se encuentra en los intervalos:\(\sigma \in \left[-2,0\right]\cup (-\infty ,-3]\) (para\(K>0)\).
3. Los puntos de ruptura del eje real están definidos por:\(\frac{1}{\sigma } +\frac{1}{\sigma +2} =\frac{1}{\sigma +3}\), o\({\sigma }^2+6\sigma +6=0\); las soluciones incluyen:\(\sigma =-1.27\) (ruptura) y\(-4.73\) (break-in).
4. El ángulo de asíntota se da como:\(\pm 180^{\circ }\) (para\(K>0\)), con intersección en:\(\sigma _{a} =1\).

La gráfica RL resultante (for\(K>0\)) se muestra en la Figura 5.1.4.

Figura\(\PageIndex{4}\): La gráfica del locus radicular para\(G(s)=\frac{(s+3)}{s(s+2)}\).

pkg load control
s=tf('s');
Gs=(s+3)/s/(s+2);
rlocus(Gs)

                                                                               
                                  Root Locus of Gs                             
                                                                               
         |-----------------------------------------------------------------|   
         |   +      +       +      +      +       ++------$$$$$$$---------+|   
     1.5 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&|###?#$$locus$$       +||   
         |   &      &       &      &      &       &|   B$$ open loop poles||   
       1 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&+---F$--zeros--$-------+|   
         |   &      &       &      &      &       &    $ &       &$$    &  |   
     0.5 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&$&&&&&&&&&&&$&&&&&+-|   
         |   &      &       &      &      &       &    $ &       & $    &  |   
       0 |**##########################################$$$$$$$F***B#$$$$$B**|   
         |   &      &       &      &      &       &   #  &       & #    &  |   
         |   &      &       &      &      &       &    # &       & #    &  |   
    -0.5 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&#&&&&&&&&&&&#&&&&&+-|   
         |   &      &       &      &      &       &    # &       &##    &  |   
      -1 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&##&&&&&&&&&#&&&&&&+-|   
         |   &      &       &      &      &       &     ##       ##     &  |   
    -1.5 |-+&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&##&&&&&##&&&&&&&+-|   
         |   +      +       +      +      +       +      +#######+      +  |   
         |-----------------------------------------------------------------|   
            -16    -14     -12    -10    -8      -6     -4      -2      0      
                          Real Axis     gain = [0, 17.4235]                    
                                                                               

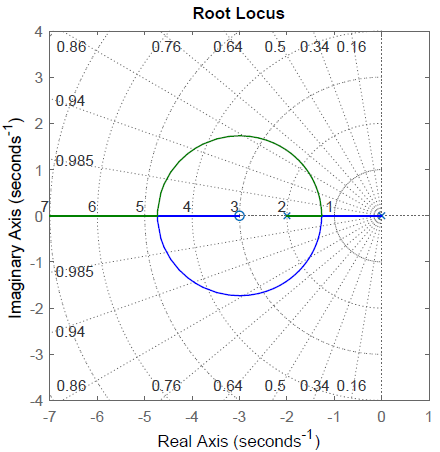
Ejemplo\(\PageIndex{4}\)

Vamos\(KGH(s)=\frac{K}{s(s+1)(s+2)}\); entonces,\(n=3,\ m=0\). El polinomio característico de bucle cerrado se forma como:\(\Delta (s)=s^{3} +3s^{2} +2s+K\).

La gráfica RL se esboza de la siguiente manera:

1. El RL tiene tres ramas que comienzan en los polos OL en\(s=0,-1,-2\) (para\(K=0)\); las ramas siguen asíntotas RL como\(K\to \infty\).
2. El locus del eje real se encuentra a lo largo\(\sigma \in \left[-1,0\right]\) (para\(K>0)\).
3. Los puntos de ruptura se dan como la solución a:\(\frac{1}{\sigma } +\frac{1}{\sigma +1} +\frac{1}{\sigma +2} =0\), que reduce a:\(3\sigma ^{2} +6\sigma +2=0\), y tiene soluciones en\(\sigma =-0.38,\; -2.62\). La primera solución es un punto de ruptura para\(K>0\); la segunda es el punto de ruptura para\(K<0\).
4. Los ángulos de asíntota se dan como:\(\pm 60^{\circ } ,180^{\circ }\) (para\(K>0\)); su punto de intersección común está en:\(\sigma _a =-\frac{3}{3} =-1\).

La gráfica RL resultante (for\(K>0\)) se muestra en la Figura 5.1.5.

Figura\(\PageIndex{5}\): La gráfica del locus radicular para\(G(s)=\frac{1}{s(s+1)(s+2)}\).

pkg load control
s=tf('s');
Gs=1/s/(s+1)/(s+2);
rlocus(Gs)

                                                                               
                                 Root Locus of Gs                              
                                                                               
       |-------------------------------------------------------------------|   
       |    +            +            +            +----------------**&&&-+|   
     2 |-+*****************************************|###?###asymptote&&&  +||   
       |    *            *            *            |%%%?%%%locus* &&&     ||   
       |    *            *            *            +---B---open loop poles+|   
     1 |-+****************************************************&&&********+-|   
       |    *            *            *            *   ***  &&& *          |   
       |    *            *            *            * **    &&   *          |   
     0 |##%%%%%%%%%%%%%%%%%%%%%%%%%%%%B############B@@@@@@@&&&&&B********+-|   
       |    *            *            *            *   $$$ @    *          |   
       |    *            *            *            *      $@@   *          |   
       |    *            *            *            *        @@@ *          |   
    -1 |-+****************************************************@@@********+-|   
       |    *            *            *            *            @@@        |   
       |    *            *            *            *            * @@@$     |   
    -2 |-+**********************************************************@@@$*+-|   
       |    +            +            +            +            +     @@@  |   
       |-------------------------------------------------------------------|   
           -4           -3           -2           -1            0              
                          Real Axis     gain = [0, 28.5]                       
                                                                               

 

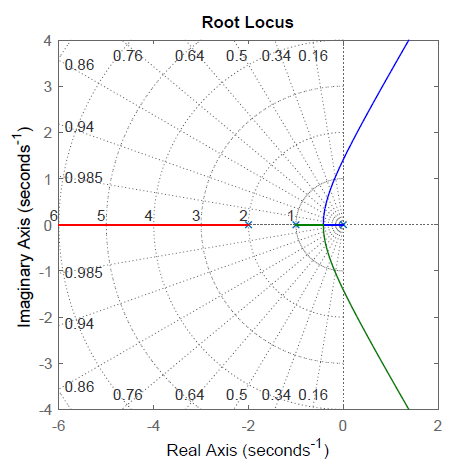
Restricciones analíticas RL

Las restricciones analíticas de RL se derivan del polinomio característico de bucle cerrado,\(\Delta (s,K)=1+KGH(s).\) que es satisfecho por las raíces de bucle cerrado del sistema de control de retroalimentación.

Así, para que un punto\(s_1\) se acueste sobre el locus radicular, debe satisfacer:\(KGH\left(s_1\right)=-1\). Además,\(KGH\left(s_1\right)\) es un número complejo de ahí que deba satisfacer:\(KGH\left(s_1\right)=1\angle 180{}^\circ\).

Para continuar, asumimos que la función de transferencia de bucle\(KGH(s)\), se escribe en la forma factorizada como:

\[KGH(s)=\frac{K(s-z_{1} )\ldots (s-z_{m} )}{(s-p_{1} )\ldots (s-p_{n} )} ;\; n>m.\]

Entonces, la magnitud correspondiente y las condiciones angulares involucran distancias y ángulos desde los polos OL y ceros hasta un punto en el RL. Las condiciones se dan como:

Definición: Condición de Magnitud

Para que un punto se encuentre en la gráfica de locus raíz, la magnitud de la función de transferencia en ese punto se limita como:\[\left|KGH(s_{1} )\right|=\frac{K\left|s_{1} -z_{1} \right|\ldots \left|s_{1} -z_{m} \right|}{\left|s_{1} -p_{1} \right|\ldots |s_{1} -p_{n} |} =1\]

Definición: Condición de ángulo

Para que un punto se encuentre en la gráfica de locus raíz, el ángulo de la función de transferencia en ese punto se limita como:\[\angle KGH(s_{1} )\; =\; \angle (s_{1} -z_{1} )+\ldots +\angle (s_{1} -z_{m} )-\angle (s_{1} -p_{1} )-\ldots -\angle (s_{1} -p_{n} )=\pm 180^{\circ } \]

Los términos individuales,\(\left|s_1-p_i\right|\) y\(\left|s_1-z_i\right|\), en la condición de magnitud representan las distancias euclidianas desde los polos de bucle abierto y ceros hasta la ubicación de los polos de bucle cerrado,\(s=s_1\).

Del mismo modo, los términos,\(\angle(s_1-p_i)\) y\(\angle(s_1-z_i)\) denotan los ángulos de la ubicación del polo designado.

Ejemplo\(\PageIndex{5}\)

Dejar\(KGH(s)=\frac{K}{s(s+1)(s+2)}\); entonces, suponiendo que un punto\(s_1=j\sqrt{2}\),, yace en el locus raíz, satisface las siguientes condiciones (Figura 5.1.6):

Condición de magnitud:\(\frac{K}{|j\sqrt{2}|\,|1+j\sqrt{2}|\,|2+j\sqrt{2}|}=1\)

Condición del ángulo:\(-\angle(j\sqrt{2})-\angle(1+j\sqrt{2})-\angle(2+j\sqrt{2})=-180^\circ\)

Figura\(\PageIndex{6}\): Desplazamientos y ángulos desde los polos OL hasta un punto en el RL.

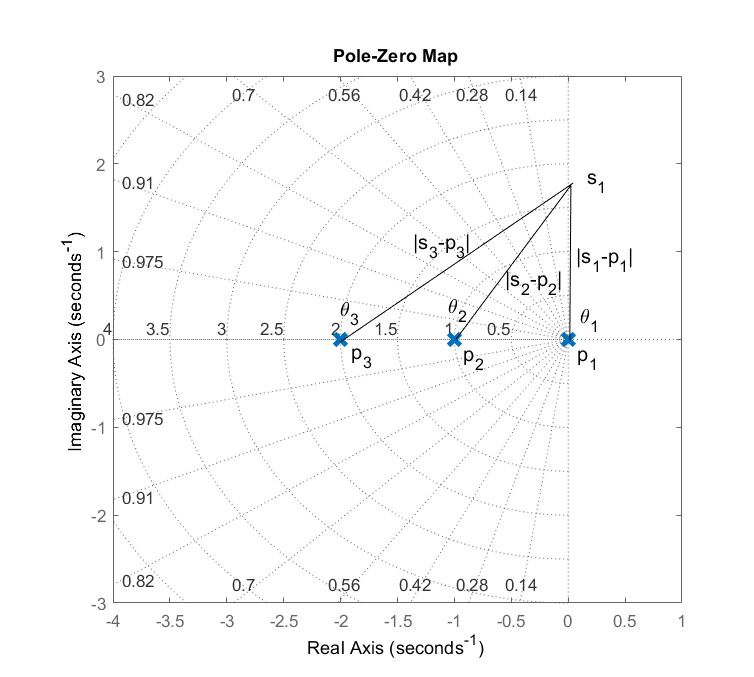
Diseño de controladores

La condición de magnitud,\(\left|KGH(s_{1} )\right|=1\), se puede resolver para la ganancia del controlador estático,\(K\), para obtener:\(K=\frac{\left|s_{1} -p_{1} \right|\ldots |s_{1} -p_{n} |}{\left|s_{1} -z_{1} \right|\ldots \left|s_{1} -z_{m} \right|}\).

Además, vamos a\(\theta _{z_{i} } ,\theta _{p_{i} }\) denotar los ángulos desde los ceros y polos de bucle abierto hasta el punto\(s_{1}\); entonces, la condición de ángulo establece que:\(\sum \theta _{z_{i} } -\sum \theta _{p_{i} } =\pm 180^{\circ }\) (for\(K>0\)). Alternativamente,\(\sum \theta _{z_{i} } -\sum \theta _{p_{i} } =0^{\circ }\) (para\(K<0\)).

La condición de ángulo se puede usar para agregar polos y ceros al bucle de retroalimentación, es decir, diseñar un controlador dinámico que obligaría a una rama RL a pasar a través de una ubicación raíz de bucle cerrado deseada.