5.3: Mejora de la Respuesta Transitoria

Mejoras del locus radicular

Un controlador dinámico altera la gráfica del locus raíz agregando polos y ceros a la función de transferencia de bucle. En general, la adición de un cero finito a la función de transferencia de bucle provoca que las ramas RL se doblen hacia ella, mientras que la presencia de un polo de bucle cerrado repele la rama RL cercana a él.

En particular, exploramos el efecto de agregar un controlador dinámico de primer orden, definido por:\(K(s)=\frac{K(s+z_{c} )}{s+p_{c} }\) al bucle de retroalimentación. Un controlador de primer orden agrega un cero\(-z_c\), y un polo\(-p_c\), a la función de transferencia de bucle.

La adición de un controlador de fase de primer orden al bucle de retroalimentación mejora la respuesta transitoria del sistema; la adición de un controlador de retardo de fase o PI mejora la respuesta de seguimiento de estado estacionario.

Diseño de controlador de plomo de fase

Para lograr mejoras en la respuesta transitoria, se puede agregar un conductor de fase o un controlador PD al bucle de retroalimentación. Un controlador de cable de fase se describe por:

\[K\left(s\right)=\frac{K\left(s+z_c\right)}{s+p_c};\ z_c<p_c\]

En el caso limitante de\(p_c\to \infty\), el controlador de cable de fase cambia a un controlador PD, descrito por:\[K\left(s\right)=K\left(s+z_c\right)\]

El controlador PD tiene ganancia ilimitada a altas frecuencias, lo que amplificaría el ruido de alta frecuencia que ingresa al sistema. Por lo tanto, para una supresión efectiva del ruido,\(p_c\gg z_c\) se prefiere un diseño de cable de fase con un controlador PD.

Las ubicaciones del polo del controlador y cero en el caso de los controladores de cable de fase y PD se seleccionan con la ayuda de la condición de ángulo RL. El procedimiento general de diseño se da de la siguiente manera:

1. Seleccione una ubicación de poste de bucle cerrado deseada,\(s_1\) a partir de las especificaciones de diseño.
2. Compute\(G\left(s_1\right)\); el comando 'evalfr' de MATLAB se puede utilizar para este propósito.
3. Utilice la condición de ángulo para determinar la contribución de ángulo requerida del controlador:\[{\theta }_z-{\theta }_p=180{}^\circ -\angle G\left(s_1\right)\]
4. Seleccione las ubicaciones de polo y cero del controlador para cumplir con la contribución de ángulo del controlador; dado que la condición de ángulo define una sola restricción entre dos variables, son posibles múltiples diseños.
5. Utilice el comando 'evalfr' de MATLAB para verificar la contribución del ángulo del controlador. Tenga en cuenta que es posible que solo necesitemos un diseño de 'estadio'.
6. Trace el locus raíz para el sistema compensado y elija ganancia\(K\) para completar el diseño del controlador.

Ejemplo\(\PageIndex{1}\): Phase-Lead Design

Dejar\(G(s)=\frac{2}{s(s+2)}\); diseñar un controlador de fase para lograr las siguientes especificaciones:\(\zeta \cong 0.7,\; \; t_ s \le 2\, s\).

El diseño del controlador de cable de fase procede de la siguiente manera:

1. Vamos a\(s_1=-2.5\pm j2.5\) describir una ubicación raíz de bucle cerrado deseada.
2. Al usar el comando 'efalfr' de MATLAB para evaluar la función de transferencia de planta, obtenemos:\(G(s_1)=0.222\angle 123.7{}^\circ\); por lo tanto, la contribución de fase del controlador requerida para realizar la ubicación deseada del polo es:\(K\left(s_1\right)=K\angle 56.3{}^\circ\).
3. Vamos\(z_c=2,\ p_c=5\); entonces,\(K\left(s_1\right)=0.72\angle 55{}^\circ\).
4. Además,\(K(s_1)G(s_1)\cong 0.16\angle 180^\circ\); de ahí,\(K=\frac{1}{0.16}\cong 6.3\). Alternativamente, a partir de la gráfica del locus raíz del sistema compensado, la ganancia del controlador se encuentra como:\(K=6.29\); por lo tanto,\(K\left(s\right)=6.29\left(\frac{s+2}{s+5}\right)\).

A continuación se muestra la gráfica de locus radicular para el diseño de fase-plomo (Fig. 5.3.1).

Figura\(\PageIndex{1}\): Locus radicular para el diseño de fase-plomo.

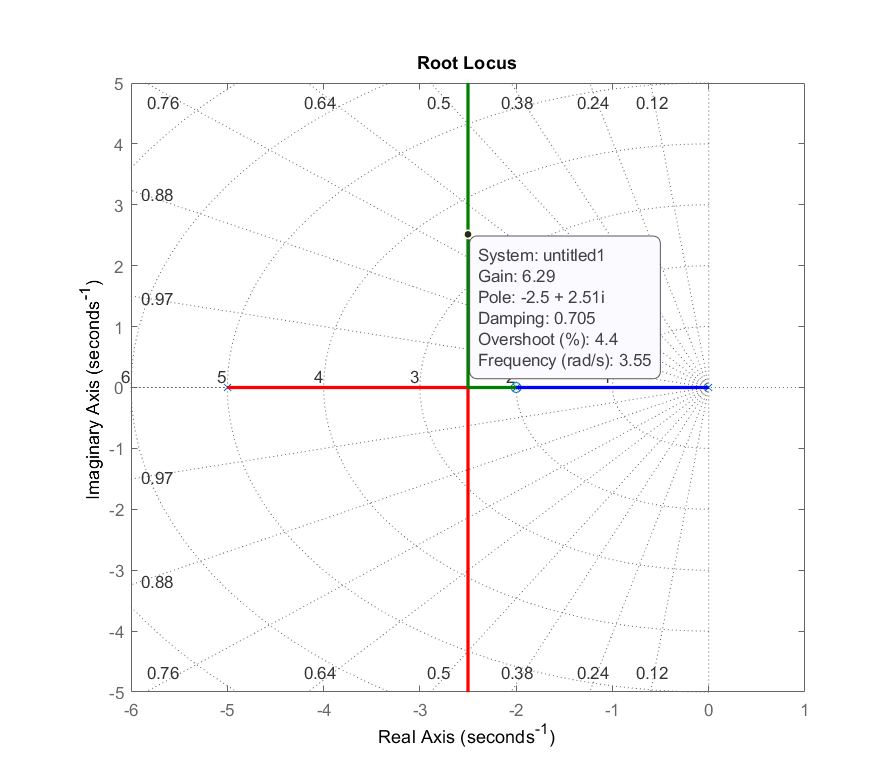
El sistema de bucle cerrado se forma como:\[T(s)=\frac{12.58(s+2)}{(s+2)(s^2+5s+12.58)}\]

Observamos que la función de transferencia de bucle cerrado\(T(s)\) incluye una cancelación polo-cero en\(s=-2\). Dichas cancelaciones están permitidas siempre y cuando estén restringidas al plano abierto de la mitad izquierda (OLHP). Además, las inexactitudes de los componentes hacen que la cancelación exacta de polo y cero sea un evento poco probable en la práctica.

La respuesta escalonada del sistema de bucle cerrado se representa en la Fig. 5.3.2. A partir de la figura, el tiempo de asentamiento se da como:\(t_s=1.7s\).

Figura\(\PageIndex{2}\): Respuesta escalonada del sistema de bucle cerrado.

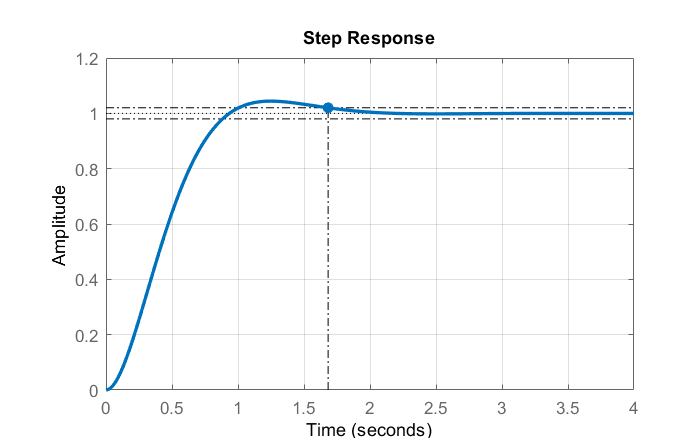
También observamos que son posibles diseños alternativos de cables de fase para este ejemplo, sin embargo,\(z_c<2\) es probable que elegir la ubicación cero del controlador aumente el tiempo de asentamiento del sistema de bucle cerrado.

Ejemplo\(\PageIndex{2}\): PD Controller Design

Dejar\(G(s)=\frac{2}{s(s+2)}\); diseñar un controlador PD para lograr las siguientes especificaciones son:\(\zeta \cong 0.7,\; \; t_ s \le 2\, s\).

El diseño del controlador PD procede de la siguiente manera:

1. Vamos a\(s_1=-2.5\pm j2.5\) describir una ubicación raíz de bucle cerrado deseada.
2. Al usar el comando 'efalfr' de MATLAB para evaluar la función de transferencia de planta, obtenemos:\(G\left(s_1\right)=0.222\angle 123.7{}^\circ\); por lo tanto, la contribución de fase del controlador requerida para realizar la ubicación deseada del polo es:\(K\left(s_1\right)=K\angle 56.3{}^\circ\).
3. De la trigonometría (Fig. 5.3.3), vamos\(z_c=4.17\); entonces, para\(K(s)=s+z_c\), tenemos:\(K(s_1)\cong 3\angle 56.3{}^\circ\).
4. Ya que\(K(s_1)G(s_1)\cong 0.66\angle 180^\circ\), tenemos\(K=\frac{1}{0.66}=1.5\). Alternativamente, a partir de la gráfica RL del sistema compensado (Fig. 5.3.4), obtenemos:\(K=1.5\); por lo tanto,\(K\left(s\right)=1.5(s+4.17)\).

Figura\(\PageIndex{3}\): Trigonometría para calcular el ángulo requerido desde el controlador cero.

Figura\(\PageIndex{4}\): Gráfica del locus raíz para el controlador PD.

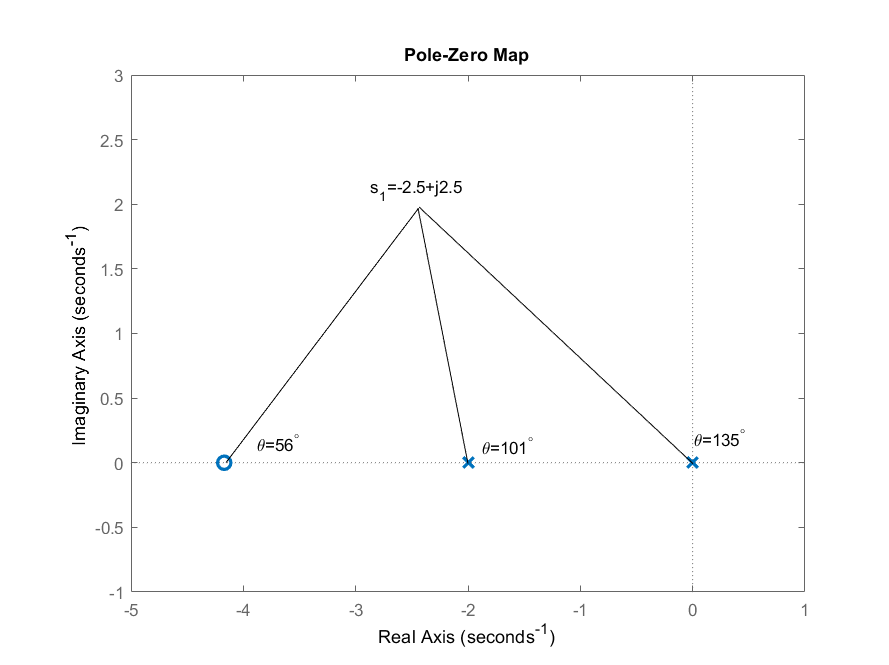
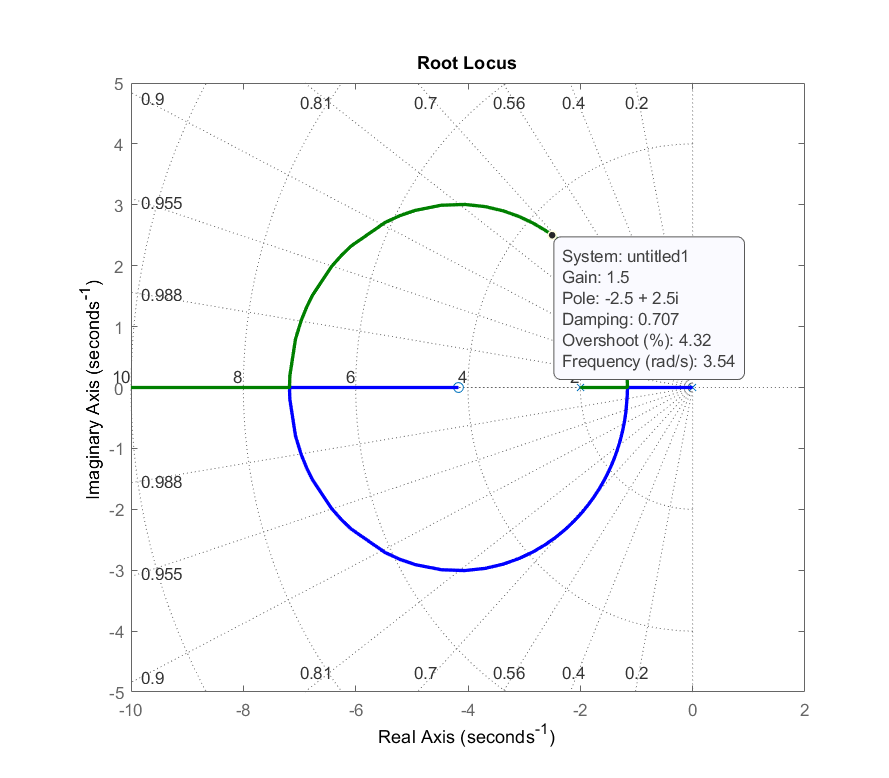
Por consideraciones de supresión de ruido, es preferible reemplazar el controlador PD por un diseño de cable de fase.

En consecuencia, vamos\(K(s)=K\frac{s+4}{s+55}\); ya que\(K(s_1)G(s_1)\cong 0.012\angle 180^\circ\), vamos\(K=81.25\). Entonces, para\(K(s)=81.25\frac{s+4}{s+55}\), tenemos\(K(s_1)G(s_1)=-1\).

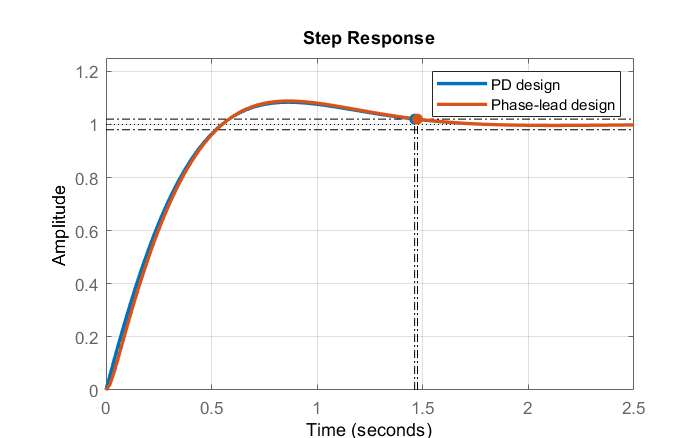
La respuesta escalonada del controlador PD y el diseño propuesto de fase de plomo son casi idénticos (Fig. 5.3.5).

Figura\(\PageIndex{5}\): Respuesta escalonada de los sistemas de bucle cerrado.

A continuación se presenta un segundo ejemplo de diseño de fase de plomo.

Ejemplo\(\PageIndex{3}\): Phase-Lead Design

Dejar\(G\left(s\right)=\frac{10}{s\left(s+2\right)(s+5)}\); asumir que las especificaciones de diseño se dan como:\(OS\le 10\%,\ \ t_s\le 2sec\).

El diseño del controlador de cable de fase procede de la siguiente manera:

1. Vamos a\(s_1=-2.2\pm j2.4\) describir una ubicación raíz de bucle cerrado deseada.
2. Usando el comando 'efalfr' de MATLAB, obtenemos:\(G\left(s_1\right)=0.35\angle 92{}^\circ\); la contribución de fase del controlador requerida es:\(K\left(s_1\right)=K\angle 88{}^\circ\).
3. Vamos\(z_c=2,\ p_c=22\); entonces\(K\left(s_1\right)=0.11\angle 88{}^\circ\).
4. A partir de la consideración de ganancia, let\(|K(s_1)G(s_1)|=1\); entonces, mediante el uso del comando 'evalfr', obtenemos\(K=24\), de ahí que el controlador de fase de plomo deseado es:\(K(s)=\frac{24(s+2)}{s+22}\). El sistema compensado tiene,\(K(s_1)G(s_1)\cong -1\).

El sistema de bucle cerrado resultante después de la cancelación polo-cero se da como:\(T\left(s\right)=\frac{240}{\left(s+22.6\right)\left(s^2+4.4s+10.62\right)}\).

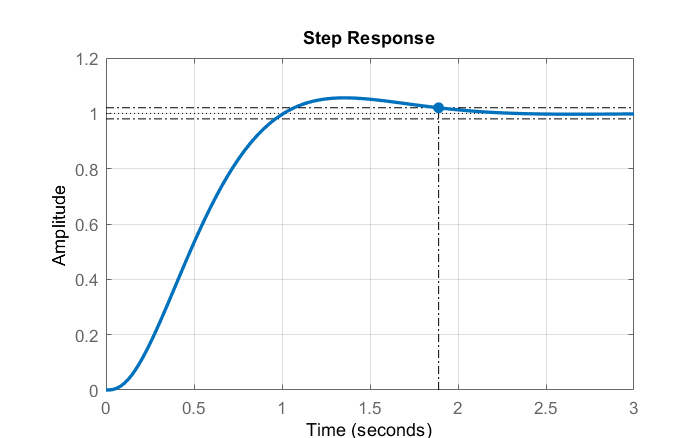
La respuesta escalonada del sistema de bucle cerrado muestra un tiempo de asentamiento de\(1.8s\).

Figura\(\PageIndex{6}\): Respuesta escalonada del sistema de bucle cerrado.

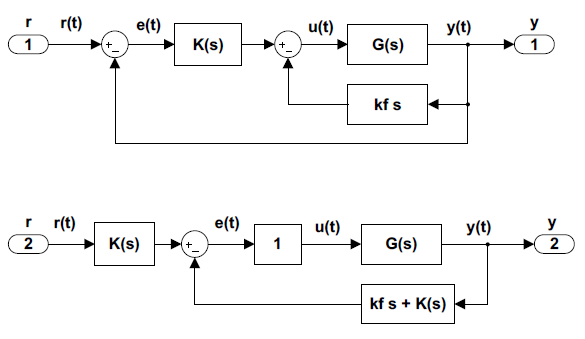
Diseño de controlador de retroalimentación de velocidad

La configuración de retroalimentación de velocidad, mostrada en la Figura 5.3.7, implica un bucle interno con retroalimentación de velocidad además de retroalimentación de salida regular. En esta configuración, la ganancia de realimentación de velocidad es\(k_f\), mientras que\(K(s)\) denota el controlador de bucle externo.

Figura\(\PageIndex{7}\): Configuración de retroalimentación de tasa (arriba); diagrama equivalente (abajo).

El diseño de retroalimentación de velocidad se realiza típicamente en dos etapas. Primero, el bucle interno está diseñado para ubicaciones de raíz de bucle cerrado adecuadas. La función de transferencia de bucle interno resultante sirve como planta para el diseño del controlador de bucle externo.

Diseño de Bucle Menor. La función de transferencia de bucle para el bucle menor se da como:\(G(s)k_ f s\). Dejar\(G(s)=\frac{n(s)}{d(s)}\); entonces, la función de transferencia de bucle menor cerrado es:\(G_{ml} (s)=\frac{n(s)}{d(s)+n(s)k_ f s} .\)

Diseño de Bucle Exterior. La función de transferencia de bucle para el bucle externo se da como:\(K(s)G_{ml} (s)\).

Dejar\(K\left(s\right)=K\); entonces, la función de transferencia de bucle externo cerrado se obtiene como:\(T\left(s\right)=\frac{Kn\left(s\right)}{d\left(s\right)+\left(k_fs+K\right)n\left(s\right)}\).

Ejemplo\(\PageIndex{4}\)

Dejar\(G(s)=\frac{2}{s(s+2)}\); asumir que las especificaciones de diseño se dan como:\(OS\le 10\%, \; t_s\le 2s \;(\zeta\ge 0.6)\).

Diseño de Bucle Menor. La ganancia de bucle menor es:\(\frac{2k_f s}{s(s+2)}\); la función de transferencia de bucle menor cerrado es:\(G_{ml} (s)=\frac{2k_f}{s(s+2+2k_f)}\).

Podemos seleccionar, por ejemplo,\(k_f=1\) para obtener:\(G_{ml} (s)=\frac{2}{s(s+4)}\).

Alternativamente, desde el locus raíz de bucle menor (Figura 5.3.8), seleccionamos\(k_f=1\) para raíz de bucle cerrado en\(s=-4\).

Figura\(\PageIndex{8}\): Locus raíz de bucle menor.

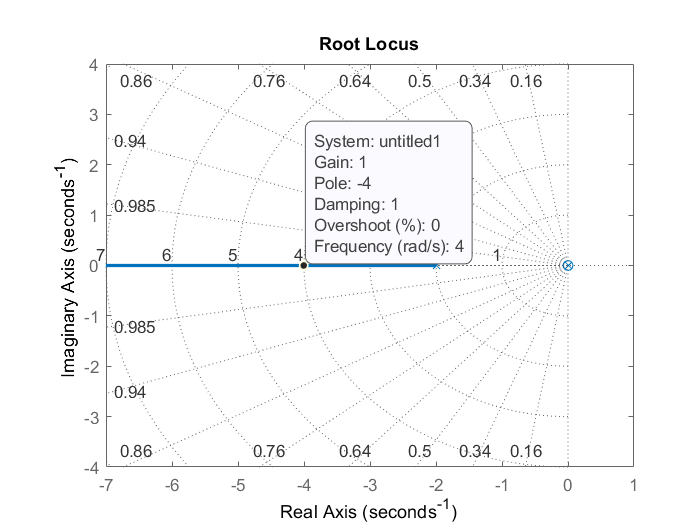
El locus raíz del bucle menor muestra una aparente cancelación polo-cero en el origen. El polo en el origen es, sin embargo, retenido en el diseño del bucle exterior.

Diseño de Bucle Exterior. La función de transferencia de bucle externo se da como:\(KG_{ml} (s)=\frac{2K}{s(s+4)}\).

Del polinomio característico de bucle cerrado,, podemos elegir\(\Delta (s)=s(s+4)+K\), p.ej.,\(K=4\), para que las raíces de bucle cerrado se ubiquen en:\(s=-2\pm j2\).

Alternativamente, podemos elegir\(K=4\) de la gráfica de locus de raíz de bucle externo (Fig. 5.3.9).

Figura\(\PageIndex{9}\): Locus radicular de bucle externo.

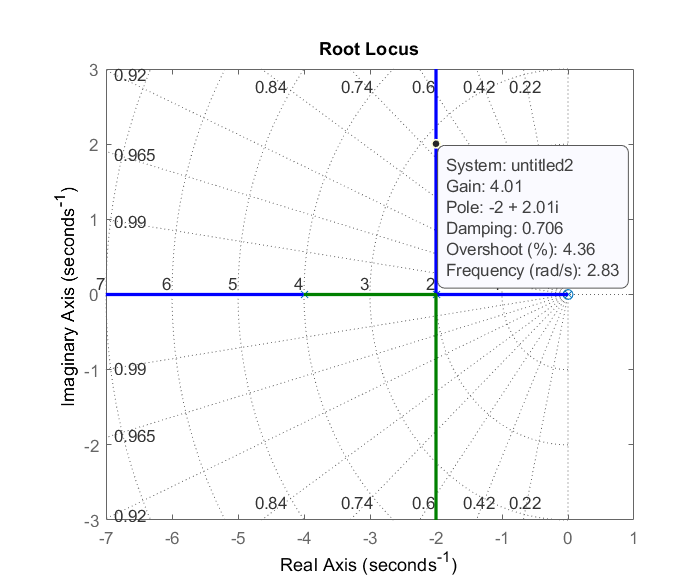
La función de transferencia de bucle externo cerrado se da como:\(T(s)=\frac{8}{s^2+4s+8}\).

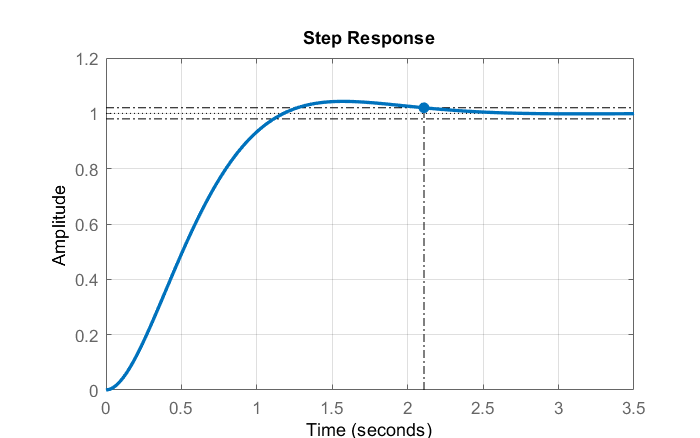
La respuesta escalonada del sistema de bucle cerrado muestra un tiempo de asentamiento de\(2.1s\).

Figura\(\PageIndex{10}\): Respuesta escalonada del sistema de bucle cerrado.

Ejemplo\(\PageIndex{5}\)

Vamos\(G(s)=\frac{10}{s(s+2)(s+5)}\); supongamos que las especificaciones de respuesta de paso son:\(OS\le 10\%,\ t_s\le 2sec \; (\zeta\ge 0.6)\).

Diseño de Bucle Menor. La ganancia de bucle menor es\(k_f s\; G(s)=\frac{10k_f s}{s(s+2)(s+5)}\). Del locus raíz de bucle menor (Figura 5.3.11), podemos elegir, por\(k_f =2\) ejemplo, que las raíces de bucle menor cerrado se ubiquen en:\(s=-3.5\pm j4.2\; (\zeta \cong 0.64)\).

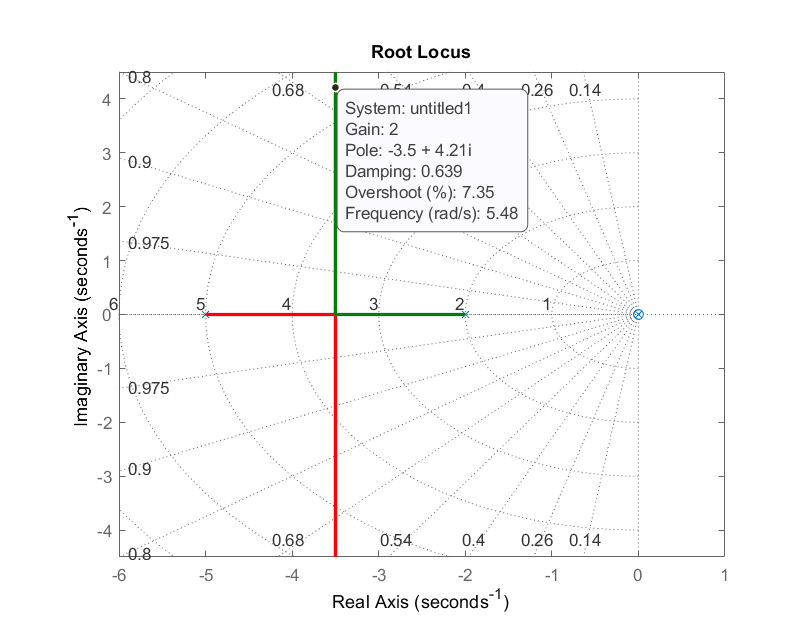
Figura\(\PageIndex{11}\): Locus raíz de bucle menor.

Diseño de Bucle Exterior. La ganancia de bucle exterior se obtiene como:\(KG_{ml} (s)=\frac{10K}{s\left[(s+2)(s+5)+k_f \right]} =\frac{10K}{s(s^{2} +7s+30)} \).

Del locus de la raíz del bucle externo, podemos elegir, p.ej.,\(K=5.4\) para raíces de bucle cerrado ubicadas en:\(s=-2\pm j3.75\; (\zeta \cong 0.47)\). Aunque\(\zeta\) parece ser baja, la respuesta escalonada del sistema de bucle cerrado tiene un pequeño sobreimpulso debido a la presencia de un polo real en\(s=-3\).

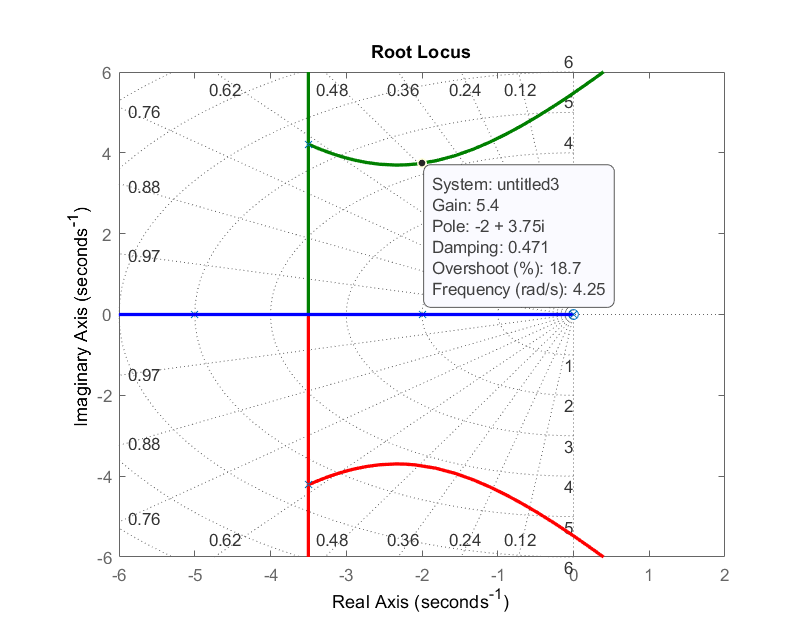
Figura\(\PageIndex{12}\): Locus radicular de bucle externo.

La función de transferencia de bucle externo cerrado se da como:\(T(s)=\frac{54}{(s+3)(s^2+4s+18)}\).

La respuesta escalonada del sistema de bucle cerrado muestra un tiempo de asentamiento de\(1.5s\).

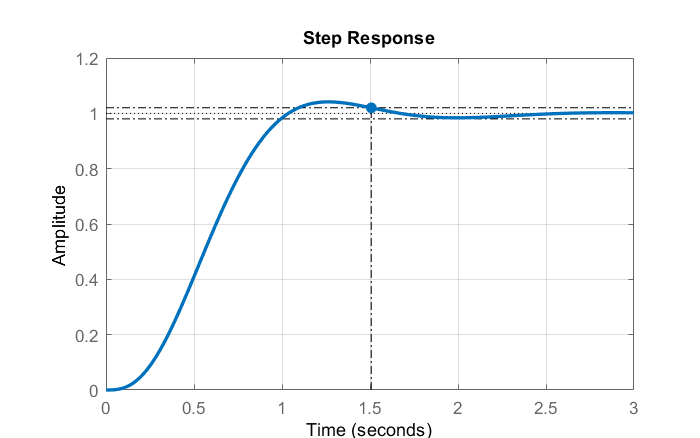
Figura\(\PageIndex{13}\): Respuesta escalonada del sistema de bucle cerrado.