5.4: Mejora de errores en estado estacionario
- Page ID
- 84941
Mejora de errores en estado estacionario
El error de seguimiento de estado estacionario a una entrada de paso o rampa se evalúa utilizando las constantes de error de posición y velocidad del sistema. Estas constantes se definen como:
\[K_ p ={\mathop{\lim }\limits_{s\to 0}}\; KGH(s)\]
\[K_{v} ={\mathop{\lim }\limits_{s\to 0}}\; sKGH(s)\]
En el caso de la configuración de retroalimentación de ganancia de unidad (\(H(s)=1\)), el error de seguimiento de estado estacionario a las entradas de paso y rampa se calcula como:
\[\left. e(\infty )\right|_{\rm step} =\frac{1}{1+K_ p }\]
\[\left. e(\infty )\right|_{\rm ramp} =\frac{1}{K_v } \]
donde el comando 'dcgain' MATLAB se puede utilizar para calcular la constante de error relevante.
La adición de un PI de primer orden o controlador de retardo de fase al bucle de retroalimentación mejora la constante de error relevante. Ambos controladores agregan un par polo-cero a la función de transferencia de bucle, y se describen por:
\[K(s)=\frac{K(s+z_ c )}{(s+p_ c )} ,\quad p_ c <z_ c \]
donde\(p_c =0\) denota el controlador PI.
Asumiendo\(K=1\), la constante de error de posición se eleva como:\(K_p^{'} =(z_c /p_c )K_p >K_p\).
El controlador PI, en particular, da como resultado:\(K_ p^{'} =\infty\), por lo tanto\(\left. e(\infty )\right|_{\rm step} =0\). En virtud de agregar un integrador al bucle de retroalimentación, el error de estado estacionario a una entrada de paso es cero para el controlador PI.
Phase Lag y diseño de PI
El diseño del controlador PI/Phase Lag tiene como objetivo aumentar la constante de error relevante sin alterar apreciablemente la gráfica RL existente.
Dejar\(s_1\) denotar una ubicación deseada de polo de bucle cerrado en la gráfica RL existente; entonces, el polo controlador y cero se seleccionan de acuerdo con:\(p_c<z_c\ll Re(s_1)\). Esto asegura que la contribución adversa del ángulo del controlador permanezca pequeña, es decir,\(\theta _ z -\theta _ p \approx 0^{\circ }\).
Las ubicaciones reales de polo-cero para el retardo de fase y la ubicación cero para PI se pueden seleccionar arbitrariamente.
El controlador PI/Phase-lag agrega un par polo-cero cerca del origen a la función de transferencia de bucle. Por lo tanto, un polo de bucle cerrado con una constante de tiempo grande aparece en la función de transferencia de bucle cerrado. Sin embargo, la contribución del modo lento agregado a la respuesta general del sistema sigue siendo pequeña debido a la proximidad del polo al cero del controlador.
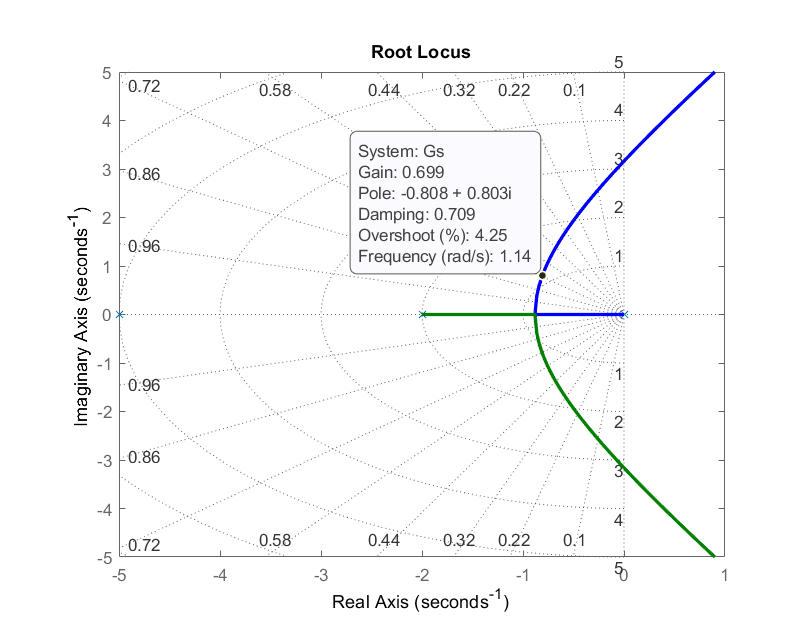
Ejemplo\(\PageIndex{1}\): Phase-Lag Design
Dejar\(G\left(s\right)=\frac{10}{s\left(s+2\right)(s+5)}\); asumir que las especificaciones de diseño se dan como:\(\zeta \ge 0.6,\ \ {e_{ss}|}_{\rm ramp}\le 0.1.\)
Dado que la mejora de la respuesta transitoria no está dirigida, podemos usar un controlador estático para satisfacer el requisito de relación de amortiguación.
Como ejemplo, vamos\(K=0.7\); entonces, el sistema de bucle cerrado tiene raíces dominantes en:\(s=-0.8\pm j0.8\; (\zeta =0.7)\). El polinomio característico se factoriza como:\(\mathit{\Delta}\left(s\right)=(s+5.38)(s^2+1.62s+1.3)\).
A continuación, la constante de error de velocidad se evalúa como:\(K_v=0.7\).
Para plantear\(K_v>10\), consideramos un controlador de retardo de fase:\(K\left(s\right)=\frac{s+0.02}{s+0.0012}\), donde\(\angle K(s_1)=-0.3{}^\circ \).
El sistema compensado tiene:\(K_v=11.67\); por lo tanto\({e_{ss}|}_{\rm ramp}\le 0.1\).
Se grafica la respuesta en rampa del sistema de bucle cerrado para confirmar los resultados.
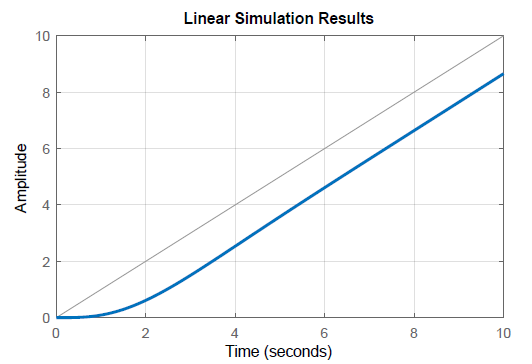
Con la adición del controlador de retardo de fase, la función de transferencia de bucle cerrado se da como:
\[T(s)=\frac{7(s+0.02)}{(s+0.0202)(s+5.38)(s^2+1.61s+1.29)}\]
La raíz de bucle cerrado en casi\(s=-0.0202\) se cancela por la presencia del cero at\(s=-0.02\). De ahí que el modo lento\(e^{-0.0202t}\) tenga un coeficiente muy pequeño y sólo afecta mínimamente la respuesta del sistema. Las raíces dominantes de bucle cerrado también se ven mínimamente afectadas.
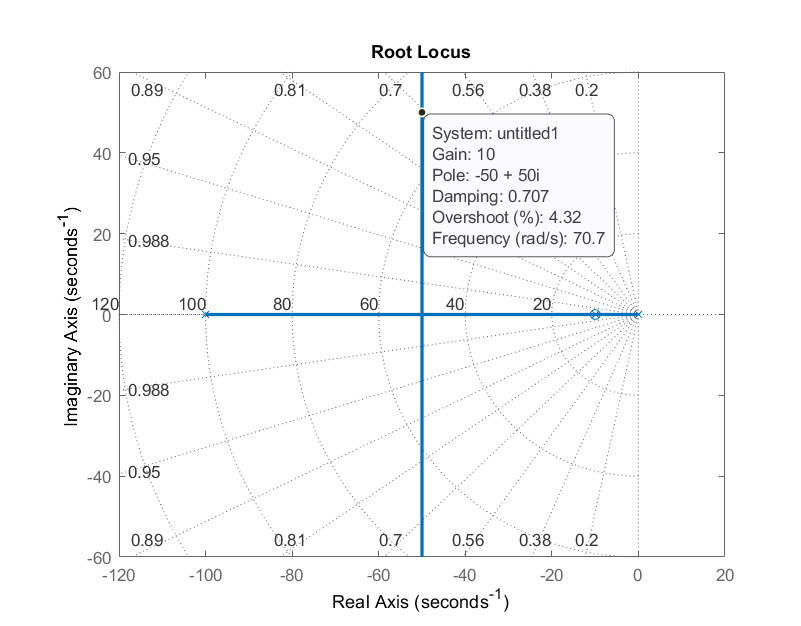
Ejemplo\(\PageIndex{2}\): PI Design
El modelo aproximado de un motor de CC se da como:\(G(s)=\frac{.5}{(.01s+1)(.1s+1)}\). Las especificaciones de diseño se dan como:\(\zeta \ge 0.6,\ \ {e_{ss}|}_{\rm step}\le 0.01.\)
Elegimos un controlador PI,\(K(s)=\frac{K(s+z_c)}{s}\), con retroalimentación de ganancia de unidad\(H(s)=1\). La ganancia de bucle se da como:\(K(s)G(s)=\frac{.5K(s+z_c)}{s(.01s+1)(.1s+1)}\).
La constante de error de posición es\(K_p=\infty\). De ahí\({e_{ss}|}_{\rm step}=0\).
El controlador cero se puede seleccionar para cancelar uno de los polos de la planta; por lo tanto\(z_c=10\). A continuación, de la parcela RL, podemos elegir, por ejemplo,\(K=10\). El diseño del controlador PI se da como:\(K(s)=\frac{10(s+10)}{s}\).
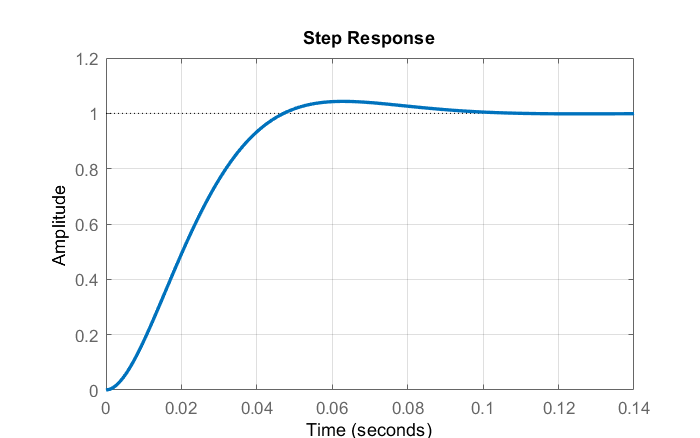
La función de transferencia del sistema de bucle cerrado se da como:\(T(s)=\frac{5000}{s^2+100s+5000}\). La respuesta escalonada del sistema de bucle cerrado se grafica a continuación.