6.1: Gráficas de Respuesta de Frecuencia

Última actualización
Guardar como PDF

Page ID: 84860

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Función de respuesta de frecuencia

La respuesta de frecuencia de la función de transferencia de bucle\(KGH(s)\),, se representa como:\(KGH(j\omega )=\left. KGH(s)\right|_{s=j\omega }\).

Para un valor particular de\(\omega\), el\(KGH(j\omega )\) es un número complejo, que se describe en términos de su magnitud y fase como\(KGH(j\omega )=|KGH(j\omega )|e^{j\phi (\omega )}\).

Como\(\omega\) varía de\(0\) a\(\infty\), se\(KGH(j\omega )\) puede trazar en el plano complejo (la gráfica polar). Alternativamente, tanto la magnitud como la fase pueden representarse como funciones de\(\omega\) (las gráficas de magnitud y fase de Bode).

Parcela de augurio

Para continuar, asumimos que la función de transferencia de bucle se expresa usando factores de primer y segundo orden como:

\[KGH(s)=\frac{K\prod _{i=1}^{m} \left(1+\frac{s}{z_{i} } \right)}{s^{n_{0} } \prod _{i=1}^{n_{1} } \left(1+\frac{s}{p_{i} } \right)\prod _{i=1}^{n_{2} } \left(1+2\zeta _{i} \frac{s}{\omega _{n,i} } +\frac{s^{2} }{\omega _{n,i}^{2} } \right)} \]

donde\(m\) está el número de ceros reales,\(n_0\) es el número de polos en el origen,\(n_1\) es el número de polos reales,\(n_2\) es el número de pares de polos complejos, y\(K\) es una ganancia escalar. Además,\(z_i\)\(p_i\) representan las frecuencias cero y polares para factores de primer orden;\(\omega _{n,i}\) y\(\zeta _i\) representan la frecuencia natural y la relación de amortiguación de factores de segundo orden.

La función de respuesta de frecuencia correspondiente se da como:

\[KGH(j\omega )=\frac{K\prod _{i=1}^{m} \left(1+j\frac{\omega }{z_{i} } \right)}{(j\omega )^{n_{0} } \prod _{i=1}^{n_{1} } \left(1+j\frac{\omega }{p_{i} } \right)\prod _{i=1}^{n_{2} } \left(1-\frac{\omega ^{2} }{\omega _{n,i}^{2} } +j2\zeta _{i} \frac{\omega }{\omega _{n,i} } \right)} \]

Se acostumbra trazar la magnitud de la función de respuesta de frecuencia en la escala logarítmica como\(|G(j\omega )|_{\rm dB} =20\; \log _{10} |G(j\omega )|\). La magnitud de la ganancia de bucle se da en dB como:

\[\begin{array}{r} {|KGH(j\omega )|_{\rm dB} =20\; \log K+\sum _{i=1}^{m} 20\; \log \left|1+\frac{j\omega }{z_{i} } \right|-(20n_{0} )\log \omega } \\ {-\sum _{i=1}^{n_{1} } 20\; \log \left|1+\frac{j\omega }{p_{i} } \right|-\sum _{i=1}^{n_{2} } 20\; \log \left|1-\frac{\omega ^{2} }{\omega _{n,i}^{2} } +j2\zeta _{i} \frac{\omega }{\omega _{n,i} } \right|.} \end{array}\]

A bajas frecuencias, la magnitud de respuesta de frecuencia es una constante, es decir,\(\lim_{\omega\to 0} |KGH(j\omega )|_{\rm dB} =20\; \log K\).

Para grandes\(\omega\), la gráfica de magnitud se caracteriza por una pendiente:\(-20(n-m)\) dB/década de\(\omega\), donde\(n-m\) representa el exceso de polo de la función de transferencia de bucle.

El ángulo\(\phi (\omega )\) de fase de la función de transferencia de bucle se calcula como:

\[\phi (\omega )=\sum _{i=1}^{m} \angle \left(1+\frac{j\omega }{z_{i} } \right)-n_{0} (90^{\circ } )-\sum _{i=1}^{n_{1} } \angle \left(1+\frac{j\omega }{p_{i} } \right)-\sum _{i=1}^{n_{1} } \angle \left(1-\frac{\omega ^{2} }{\omega _{n,i}^{2} } +j2\zeta _{i} \frac{\omega }{\omega _{n,i} } \right).\]

El ángulo de fase para grandes\(\omega\) se da como:\(\phi (\omega )=-90^{\circ } (n-m)\).

En MATLAB Control Systems Toolbox, la gráfica Bode se obtiene utilizando el comando 'bode', que se invoca después de definir el objeto de función de transferencia.

Parcela Nyquist

La función de respuesta de frecuencia\(KGH(j\omega )\) representa una función racional compleja de\(\omega\). La función se puede trazar en el plano complejo. Una gráfica polar describe la gráfica de\(KGH(j\omega )\)\(\omega\) varía de\(0\to \infty\).

La gráfica Nyquist es una curva cerrada que describe una gráfica de\(KGH(j\omega )\) for\(\omega \in \left(-\infty ,~\infty \right)\). En MATLAB Control Systems Toolbox la gráfica Nyquist se obtiene invocando el comando 'nyquist', invocado después de definir la función de transferencia.

La forma de la gráfica Nyquist depende de los polos y ceros de\(KGH(j\omega )\); se puede representar estimando magnitud y fase de\(KGH(j\omega )\) a frecuencias bajas y altas. Por ejemplo, si no\(KGH(s)\) tiene polos en el origen, entonces a baja frecuencia,\(KGH(j0)\cong K\angle 0^{\circ }\); mientras que, a alta frecuencia,\(|KGH(j\infty )|\to 0\), y\(\angle KGH(j\infty )=-90^{\circ } (n-m)\), donde\(n-m\) representa el exceso de polos de\(KGH(s)\).

En particular, para\(n-m=3\), la gráfica Nyquist cruza el eje real negativo en la frecuencia de cruce de fase,\({\omega }_{pc}\). Dejar\(G\left(j{\omega }_{pc}\right)=g\angle 180{}^\circ\); entonces, el margen de ganancia se da como\(g^{-1}\). Además, para\(K=g^{-1}\), la gráfica Nyquist de\(KG\left(j\omega \right)\) pases a través del\(-1+j0\), descrita como el punto crítico para la determinación de la estabilidad.

Definición: Criterio de Estabilidad Nyquist

El número de polos inestables de bucle cerrado de\(\Delta (s)=1+KGH(s)\) es igual al número de polos inestables de bucle abierto de\(KGH(s)\) más el número de cercos en sentido horario (CW) del\(-1+j0\) punto en el plano complejo por la gráfica Nyquist de\(KGH(s)\).

Ejemplos

Ejemplo\(\PageIndex{1}\)

Vamos\(G(s)=\frac{1}{s+1}\); entonces,\(G(j\omega )=\frac{1}{1+j\omega } =\frac{1}{\sqrt{1+\omega ^{2} } } \; \angle -\tan ^{-1} \omega\).

En particular, en puntos específicos,\(G(j0)=1\; \angle 0^{\circ }\),\(G\left(j1\right)=\frac{1}{\sqrt{2}}\angle -45{}^\circ\), y\(G(j\infty )=0\; \angle -90^{\circ }\).

La gráfica de magnitud Bode (Figura 6.1.1) comienza\(0\ dB\) con una pendiente inicial de cero que cambia gradualmente a\(-20\ dB\) por década a altas frecuencias. Una gráfica de Bode asintótica consta de dos líneas que unen ar la frecuencia de esquina (1 rad/s).

La gráfica de fase Bode varía de\(0{}^\circ\) a\(-90{}^\circ\) con una fase de frecuencia\(\ -45{}^\circ\) en la esquina.

La gráfica Nyquist de\(G\left(s\right)\) es círculo en el plano de la mitad derecha (RHP). Además, para\(K>0\), la gráfica Nyquist de\(KG\left(j\omega \right)\) está confinada al RHP; de ahí que, por criterio de estabilidad de Nyquist, el sistema de bucle cerrado sea estable para todos\(K>0\).

Ejemplo\(\PageIndex{2}\)

Vamos\(G(s)=\frac{1}{s(s+1)}\); entonces,\(G(j\omega )=\frac{1}{j\omega (1+j\omega )} =\frac{1}{\omega } \frac{1}{\sqrt{1+\omega ^{2} } } \angle -90^{\circ } -\tan ^{-1} \omega \).

En particular,\(G\left(j0\right)=\infty \angle -90{}^\circ\),\(G\left(j1\right)=\frac{1}{\sqrt{2}}(-3dB)\angle -135{}^\circ\),\(G\left(j\infty \right)=0\angle -180{}^\circ\).

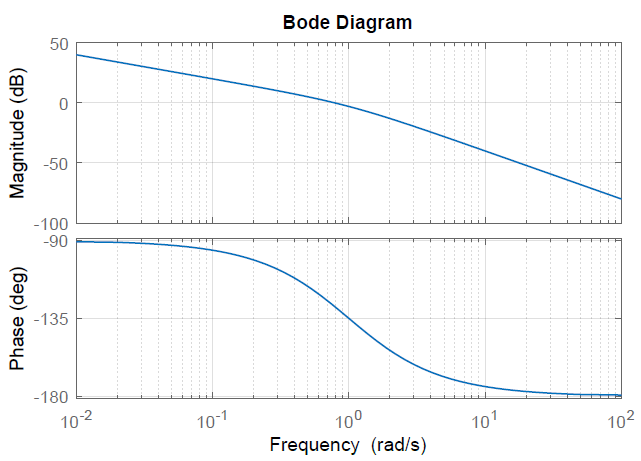
La gráfica de magnitud Bode (Figura 6.1.2) tiene una pendiente inicial\(-20\ dB\) por década que cambia gradualmente a\(-40\ dB\) por década a altas frecuencias. La gráfica de fases muestra una variación de\(-90{}^\circ\) a\(-180{}^\circ\) con una fase de frecuencia\(\ -135{}^\circ\) en la esquina.

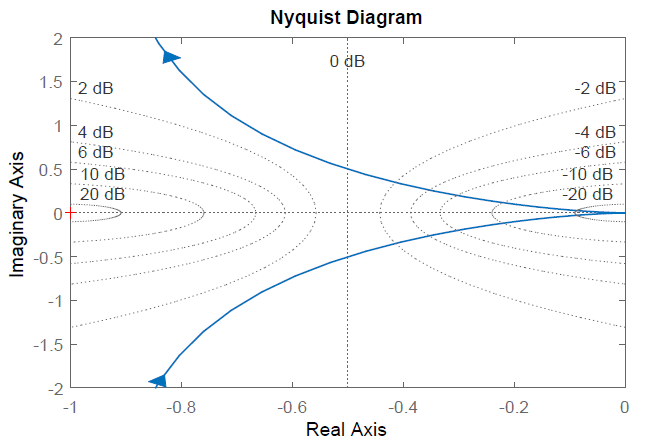
La gráfica Nyquist es una curva cerrada que viaja a lo largo\(j\omega\) del eje negativo para\(\omega \in (0,\infty )\), a lo largo\(j\omega\) del eje positivo para\(\omega \in (-\infty ,0)\), y escriba un semicírculo de un radio grande para\(\omega \in \left(0^-,0^+\right)\). A medida que la gráfica de Nyquist\(KG\left(j\omega \right)\) se mantiene alejada del punto crítico (\(-1+j0\)) para valores positivos de\(K\), se proyecta que el sistema de bucle cerrado sea estable para todos\(K>0\).

Figura\(\PageIndex{2}\): Parcelas Bode y Nyquist para\(G\left(s\right)=\frac{1}{s\left(s+1\right)}\).

Ejemplo\(\PageIndex{3}\)

Vamos\(G\left(s\right)=\frac{1}{s^2+s+1}\); entonces,\(G\left(j\omega \right)=\frac{1}{1-{\omega }^2+j\omega }=\frac{1}{\sqrt{\left(1-{\omega }^2\right)^2+\left(\omega \right)^2}} \angle -{tan}^{-1} \frac{\omega }{1-{\omega }^2}\).

En particular,\(G\left(j0\right)=1\left(0dB\right)\angle 0{}^\circ\),\(G\left(j1\right)=1\left(0dB\right)\angle -90{}^\circ\),\(G\left(j\infty \right)=0\angle -180{}^\circ\).

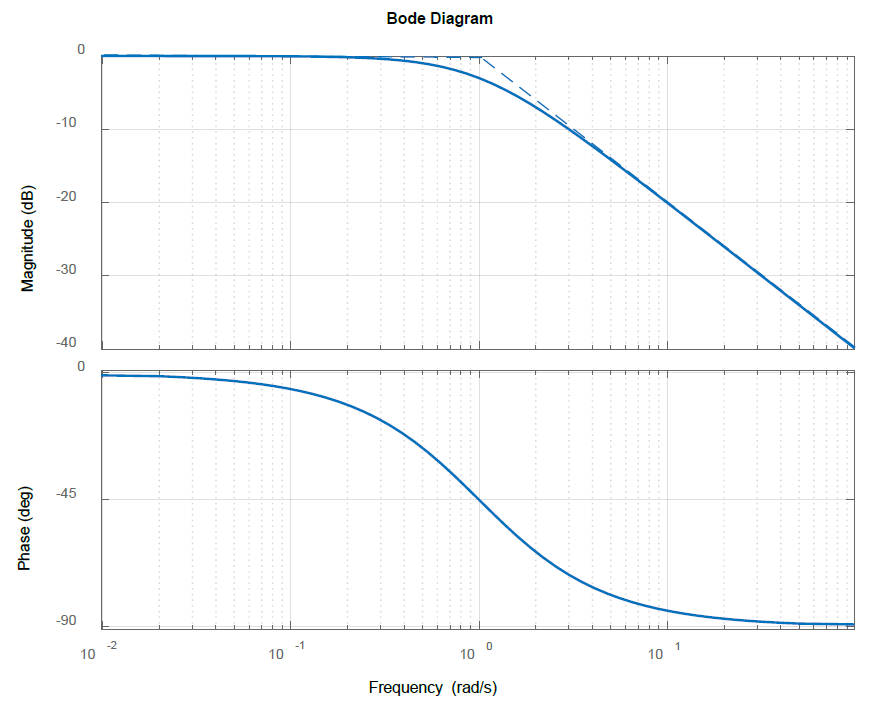
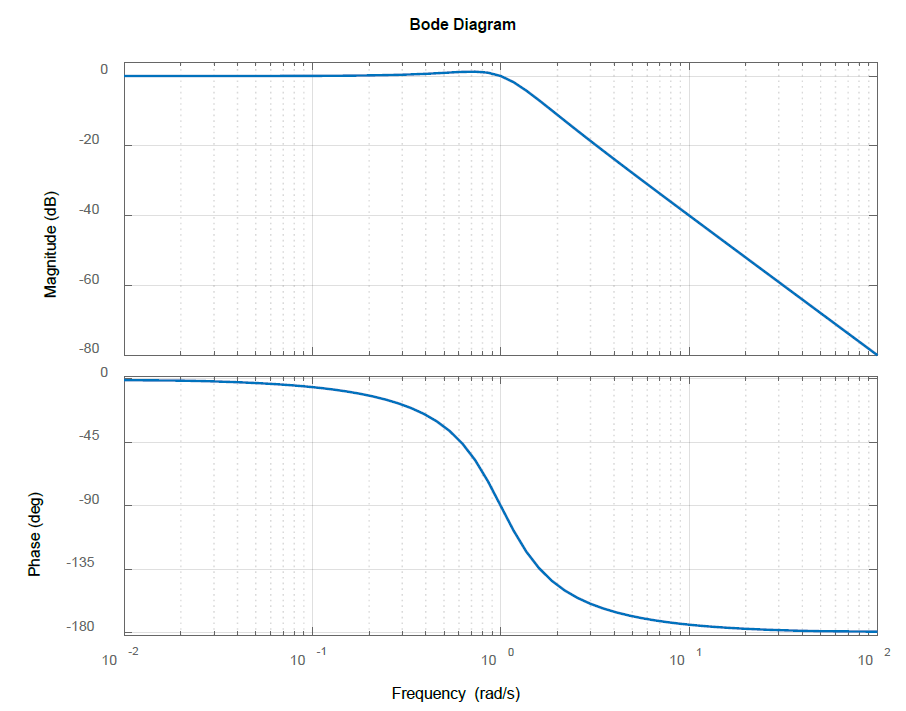
La gráfica de magnitud Bode (Figura 6.1.3) comienza en\(0\ dB\) con una pendiente inicial de 0; la pendiente cambia a\(-40\ dB\) por década para\(\omega >1\). La gráfica de magnitud muestra un pico de resonancia en la frecuencia de esquina debido al bajo valor de\(\zeta=0.5\).

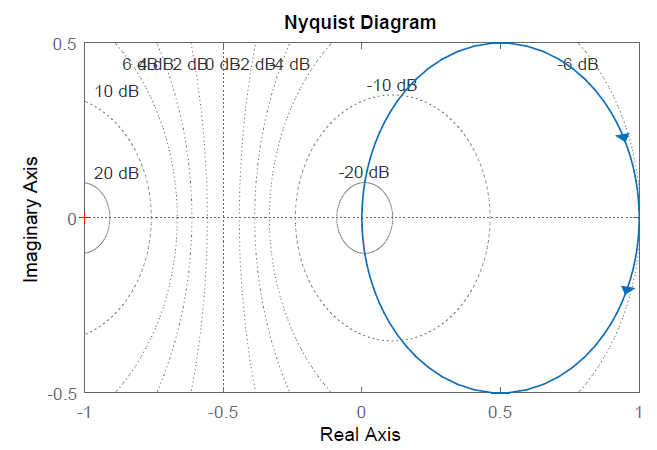
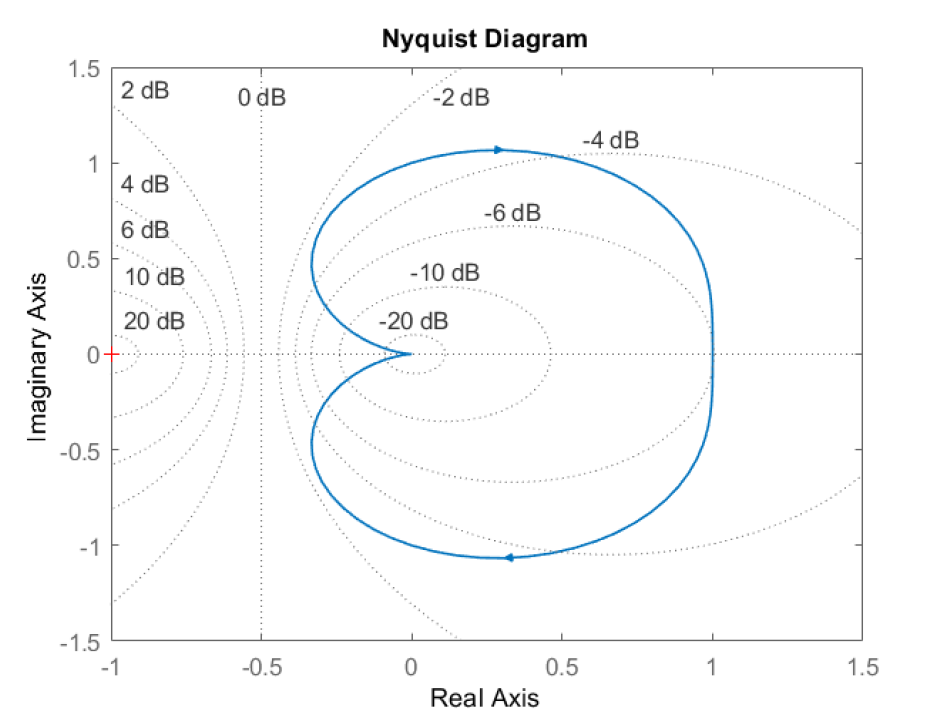
La gráfica Nyquist de\(G\left(j\omega \right)\) es una curva cerrada que no tiene cruce con el eje real negativo. A medida que la gráfica Nyquist\(KG\left(j\omega \right),\ K>0\) se mantiene alejada del punto crítico (\(-1+j0\)), se proyecta que el sistema de bucle cerrado sea estable para todos\(K>0\).

Ejemplo\(\PageIndex{4}\)

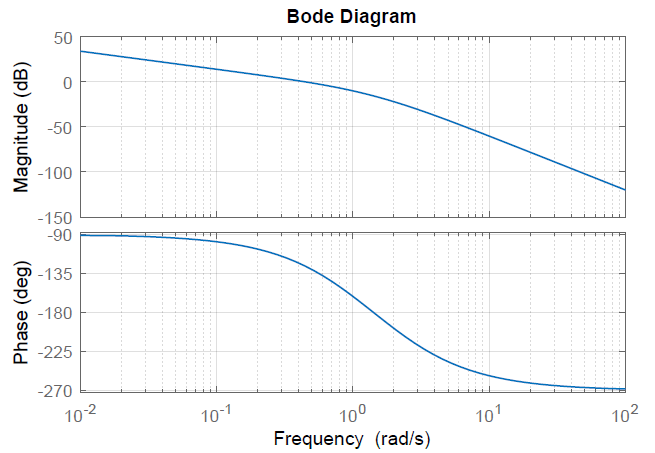
Vamos\(G(s)=\frac{2}{s(s+1)(s+2)}\); entonces,\(G(j\omega )=\frac{2}{j\omega (1+j\omega )(2+j\omega )} =\frac{1}{\omega } \frac{1}{\sqrt{1+\omega ^{2} } } \frac{2}{\sqrt{2+\omega ^{2} } } \; \angle -90^{\circ } -\tan ^{-1} \omega -\tan ^{-1} 2\omega . \nonumber\).

En particular,\(G\left(j0\right)=\infty \angle -90{}^\circ\),\(G\left(j1\right)=\frac{2}{\sqrt{10}}\left(-4dB\right)\angle -108{}^\circ\),\(G\left(j1\right)=\frac{1}{5\sqrt{2}}\left(-13dB\right)\angle -139{}^\circ\), y\(G\left(j\infty \right)=0dB\angle -270{}^\circ\).

La gráfica de magnitud Bode (Figura 6.1.4) tiene una pendiente inicial\(-20\ dB\) por década que cambia primero a\(-40\ dB\) por década y luego a\(-60\ dB\) /década a altas frecuencias. La gráfica de fases muestra una variación de\(-90{}^\circ\) a\(-270{}^\circ\).

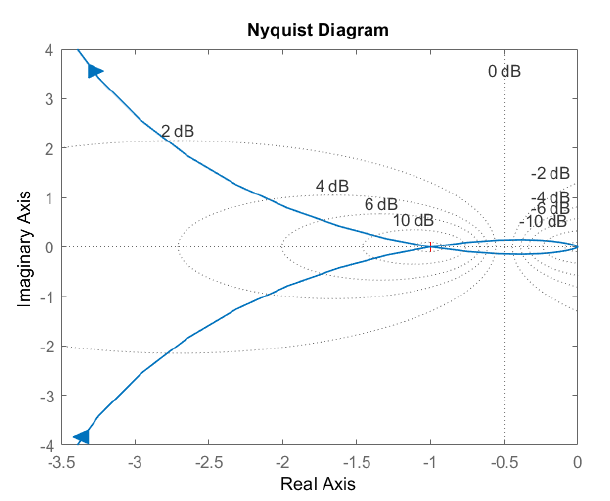
La gráfica polar comienza con una gran magnitud a lo largo del\(j\omega\) eje negativo (for\(\omega =0^+\)), cruza el eje real negativo en\(0.33\angle 180{}^\circ\) (for\(\omega =3.32\)) y se acerca al origen desde el\(j\omega\) eje positivo (for\(\omega \to\infty\)).

La parcela Nyquist, obtenida al unir un reflejo de la parcela polar, incluye un contorno cerrado que incluye un cruce negativo de eje real en\(0.33\angle 180{}^\circ\). A medida que la trama se expande\(K>1\), encierra el punto crítico (\(-1+j0\)). Se proyecta que el sistema de circuito cerrado sea estable para\(K<3\).

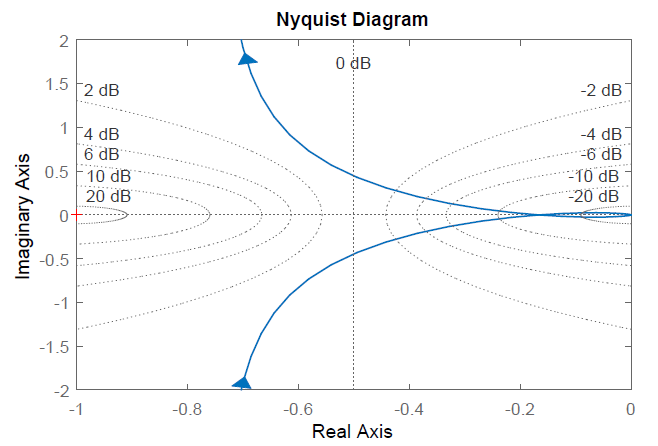
Además, la gráfica Nyquist para los\(K=3\) pases por el punto crítico.

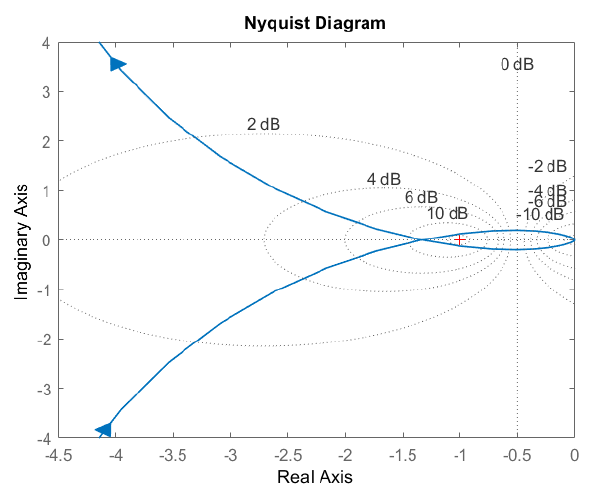
La gráfica Nyquist para\(K=4\) cruza el eje real a la izquierda del punto crítico como se muestra en la siguiente figura. Además, la gráfica de\(KGH(j\omega)\) for\(s\in(0^-,0^+)\) suscribe un círculo grande en el plano complejo (no mostrado en la figura). De ahí que la gráfica Nyquist complete dos cercos CW del punto crítico, indicando dos raíces inestables de bucle cerrado.