6.4: Respuesta de frecuencia de bucle cerrado
- Page ID
- 84869
Respuesta de frecuencia de bucle cerrado
La respuesta de frecuencia de bucle cerrado revela información importante sobre la estabilidad relativa y la velocidad de respuesta en el dominio del tiempo. Para la configuración de retroalimentación de ganancia unitaria\((H(s)=1)\), la respuesta de frecuencia de bucle cerrado se calcula como:
\[T(j\omega )=\dfrac{KG(j\omega )}{1+KG(j\omega )}\]
Para continuar, utilizamos la expresión de forma rectangular para la respuesta de frecuencia de bucle abierto:\(KG(j\omega )=X(j\omega )+jY(j\omega )\); entonces,
\[T(j\omega )=\dfrac{X+jY}{\left(1+X\right)+jY} =Me^{j\phi }\]
y
\[\left|T(j\omega )\right|^{2} =\dfrac{X^{2} +Y^{2} }{\left(1+X\right)^{2} +Y^{2} } =M^{2}.\]
Este último puede ser reorganizado para obtener:
\[\left(X+\frac{M^{2} }{M^{2} -1} \right)^{2} +Y^{2} =\dfrac{M^{2} }{(M^{2} -1)^{2} } .\]
La relación anterior representa la ecuación de un círculo con centro en\(X=\frac{M^{2} }{1-M^{2} } ,\, \, Y=0\), y radio\(r=\frac{M}{1-M^{2} }\); estos se describen como\(M\) círculos constantes en la gráfica de respuesta de frecuencia. Además, as\(M\to 1,\, \, X=-\frac{1}{2}\), que es una línea vertical que separa los círculos para\(M<1\) de aquellos con\(M>1\).
La relación de fase revela de manera similar una ecuación para círculos de fase constantes:
\[\left(X+\frac{1}{2} \right)^{2} +\left(Y-\frac{1}{2N} \right)^{2} =\frac{1}{4} +\left(\frac{1}{2N} \right)^{2}\]
donde\(N=\tan \phi\). Los círculos de fase constante están centrados en:\(X=-\frac{1}{2} ,\, \, Y=\frac{1}{2N}\), y tienen radio:\(r=\sqrt{\frac{1}{4} +\left(\frac{1}{2N} \right)^{2} }\).
Pico de Resonancia
El pico de resonancia en la respuesta de frecuencia ocurre a\(\omega =\omega _{r}\) for\(\zeta <0.7\). En particular, para un prototipo de sistema de segundo orden, tenemos:
Frecuencia resonante:\(\omega _{r} =\omega _{n} \sqrt{1-2\zeta ^{2} }\)
Pico resonante:\(M_{r} =\left|T(j\omega _{r} )\right|=\frac{1}{2\zeta \sqrt{1-\zeta ^{2} } }\)
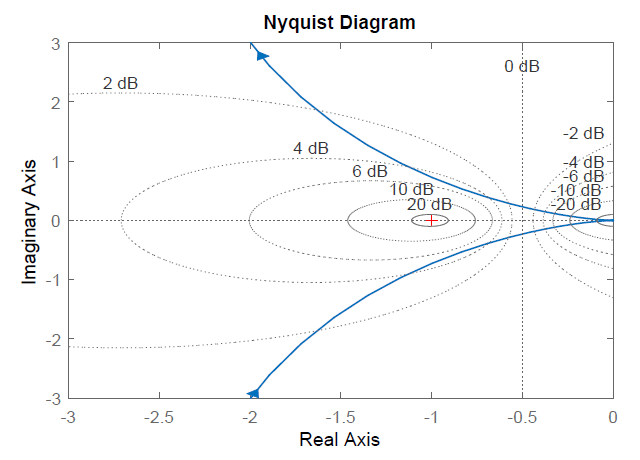
Cuando la gráfica polar de la ganancia de bucle\(KGH(j\omega )\),, se superpone a los\(N\) contornos constantes\(M\) y constantes, revela el pico de magnitud\(M_{r}\) en\(T(j\omega )\). El comando 'grid' de MATLAB Control System Toolbox agrega\(M,N\) contornos constantes en la gráfica Nyquist.
El pico de resonancia en la respuesta de frecuencia de bucle cerrado representa una medida de estabilidad relativa; la frecuencia resonante sirve como medida de la velocidad de respuesta en el dominio del tiempo. Un valor de\(M_{r} =1.3\)\((or\ 2.5dB)\) se considera un buen compromiso entre velocidad y estabilidad.
La carta de Nichol
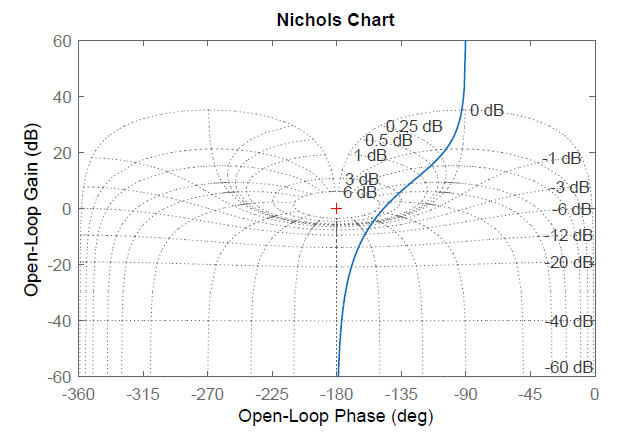
La respuesta de frecuencia de bucle cerrado se puede visualizar alternativamente en el gráfico de Nichol, donde la magnitud en dB se traza a lo largo del eje vertical, y la fase en grados se traza a lo largo del eje horizontal.
El comando 'grid' de MATLAB Control System Toolbox agrega de manera similar\(M,N\) contornos constantes en el gráfico de Nichol.
Ejemplo\(\PageIndex{1}\)
Dejar\(KG(s)=\frac{10}{s(s+1.86)}\),\(KG(j\omega )=\frac{10}{-\omega ^{2} +j1.86\omega } \);
entonces, la respuesta de frecuencia de bucle cerrado tiene un pico\(M_{r} =5\; \rm dB\), como se puede observar tanto en la gráfica de Nyquist como en la gráfica de Nichol en la Figura 6.4.1 (un\(5\rm dB\) círculo imaginario toca la\(KG(j\omega )\) curva).