8.3: Realización Estado-Espacio de Modelos de Funciones de Transferencia

Diagramas de simulación

Consideramos el problema de realizar un modelo de función de transferencia dado como un modelo de variable de estado. El proceso de realización se facilita dibujando primero un diagrama de simulación para el sistema.

Un diagrama de simulación realiza un modelo ODE en una representación de diagrama de bloques usando ganancias escalares, integradores, nodos sumadores y bucles de retroalimentación. Históricamente, dichos diagramas se utilizaron para simular modelos de sistemas dinámicos en computadoras analógicas.

Dado un modelo de función de transferencia, sus dos realizaciones comunes se describen a continuación.

Realización en serie

Se puede usar una cadena serie de integradores para realizar la salida de una ODE. Para ilustrar esta idea, consideramos un modelo general de sistema de segundo orden descrito como:

\[\frac{y\left(s\right)}{u\left(s\right)}=\frac{K}{s^2+2\zeta {\omega }_ns+{\omega }^2_n}\]

La función de transferencia se convierte en una representación ODE mediante multiplicación cruzada seguida de transformada inversa de Laplace para obtener:

\[\ddot{y}\left(t\right)+2\zeta {\omega }_n\dot{y}\left(t\right)+{\omega }^2_ny\left(t\right)=Ku\left(t\right)\]

La ecuación anterior se reordena para formar la derivada más alta como:

\[\ddot{y}\left(t\right)=-2\zeta {\omega }_n\dot{y}\left(t\right)-{\omega }^2_ny\left(t\right)+Ku\left(t\right)\]

El diagrama de simulación primero realiza la derivada más alta usando un nodo sumador y luego usa una serie de integradores para obtener las derivadas de orden inferior hasta la salida (Figura 8.3.1).

Figura\(\PageIndex{1}\): Realización en serie de una función de transferencia de segundo orden.

Realización Paralelo

Considere una función de transferencia de segundo orden con raíces reales expresadas como:\[\frac{y\left(s\right)}{u\left(s\right)}=\frac{K}{s^2+\left(\sigma_1+\sigma_2\right)s+\sigma_1\sigma_2}\]

La función de transferencia se puede expandir usando expansión parcial de fracciones (PFE) para obtener:\[y(s)=\frac{K_1}{s+\sigma_1}u(s)+\frac{K_2}{s+\sigma_2}u(s)\]

En realización paralela, la salida del sistema se expresa como:\(y\left(s\right)=y_1\left(s\right)+y_2\left(s\right)\); además, los dos componentes de salida están formados por ODEs que comparten una entrada común,\(u\left(t\right)\):\[\sigma_i{\dot{y}}_i\left(t\right)+y_i\left(t\right)=K_iu\left(t\right),\ \ i=1,2\]

Estas ODE se realizan en un diagrama de simulación paralelo (Figura 8.3.2).

Figura\(\PageIndex{2}\): Realización paralela de una función de transferencia de segundo orden.

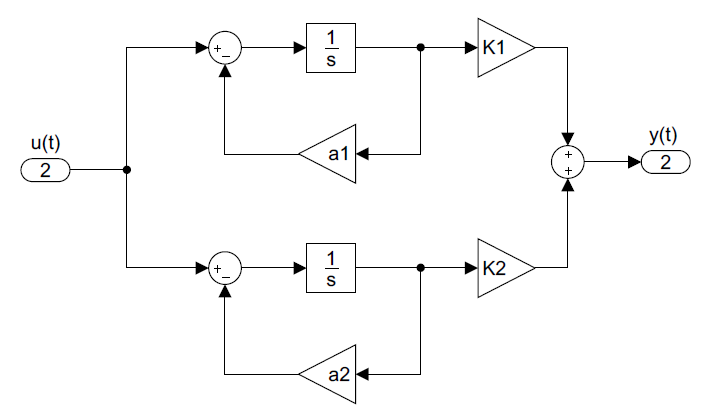
Habiendo dibujado un diagrama de simulación, designamos las salidas de los integradores como variables de estado y expresamos las entradas del integrador como ecuaciones diferenciales de primer orden, denominadas ecuaciones de estado. Una realización en serie adquiere una estructura de forma de controlador; una realización paralela adquiere una estructura modal. Estos se discuten a continuación.

Realización de Forma de Controlador

Una estructura variable de estado de forma de controlador resulta de una realización en serie del modelo de función de transferencia. Esto se ilustra usando un modelo de función de transferencia de tercer orden:

\[G(s)=\frac{b_{1} s^{2} +b_{2} s+b_{3} }{s^{3} +a_{1} s^{2} +a_{2} s+a_{3} } \]

La función de transferencia anterior corresponde a la siguiente ODE:

\[\stackrel{...}{y}(t)+a_{1} \ddot{y}(t)+a_{2} \dot{y}(t)+a_{3} y(t)=b_{1} \ddot{u}(t)+b_{2} \dot{u}(t)+b_{3} u(t)\]

Para eliminar las derivadas de la entrada de las variables de estado, se introduce una variable auxiliar\(v(t)\),, para dividir la ODE como:

\[\stackrel{...}{v}(t)+a_{1} \ddot{v}(t)+a_{2} \dot{v}(t)+a_{3} v(t)=u(t)\]\[y(t)=b_{1} \ddot{v}(t)+b_{2} \dot{v}(t)+b_{3} v(t)\]

El término derivado más alto en la primera ODE se realiza usando un nodo sumador:

\[\stackrel{...}{v}(t)=-a_{1} \ddot{v}(t)-a_{2} \dot{v}(t)-a_{3} v(t)+u(t)\]

Los términos derivados de orden inferior\(\dot{v}(t)\),\(\ddot{v}(t)\) y, y la salida\(v\left(t\right)\), se realizan utilizando integradores.

La segunda ODE se puede realizar sumando las salidas de los integradores utilizando coeficientes como ponderaciones (Figura 8.3.3).

Figura\(\PageIndex{3}\): Diagrama de simulación para la realización de forma de controlador del modelo de función de transferencia.

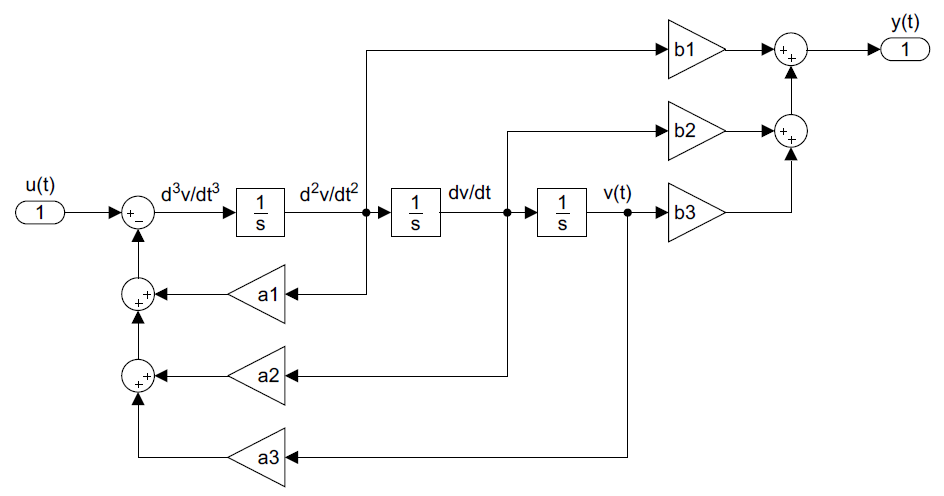
A continuación, las variables de estado se designan como:\(x_{1} (t)=v(t),\; x_{2} (t)=\dot{v}(t),\; x_{3} (t)=\ddot{v}(t)\).

Las ecuaciones de estado resultantes son:\[{\dot{x}}_1=x_2, \\ {\dot{x}}_2=x_3, \\ {\dot{x}}_3=-a_3x_1-a_2x_2-a_3x_3+u\]

La ecuación de salida se da como:\[y=b_1x_1+b_2x_2+b_3x_3\]

En forma vector—matriz, el modelo de variable de estado se da como:

\[\frac{d}{dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]=\left[\begin{array}{ccc} {0} & {1} & {0} \\ {0} & {0} & {1} \\ {-a_{3} } & {-a_{2} } & {-a_{1} } \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]+\left[\begin{array}{c} {0} \\ {0} \\ {1} \end{array}\right]u,\;\; y=\left[\begin{array}{ccc} {b_{1} } & {b_{2} } & {b_{3} } \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]\]

Generalización a\(n\) Variables

La realización de la forma controladora se generaliza a\(n\) las variables de la siguiente manera: let\(G\left(s\right)=\frac{n\left(s\right)}{d\left(s\right)}\), donde\(d(s)=s^{n} +a_{1} s^{n-1} +\ldots +a_{n-1} s+a_{n} \) representa el polinomio denominador.

Seleccionando la variable de salida y sus derivadas:\(y(t),\dot{y}(t),\ldots ,y^{(n-1)} (t)\), como variables de estado, obtenemos la siguiente estructura de forma de controlador:

\[A=\left[\begin{array}{cc} {\begin{array}{cc} {0\; \; \; \; \; \; \; } & {1} \\ {0\; \; \; \; \; \; \; } & {0} \end{array}} & {\begin{array}{cc} {0\; \; \; } & {\ldots } \\ {1\; \; \; } & {\ldots } \end{array}} \\ {\begin{array}{cc} {\vdots } & {\vdots } \\ {-a_{n} } & {-a_{n-1} } \end{array}} & {\begin{array}{cc} {\ddots } & {1} \\ {\ldots } & {-a_{1} } \end{array}} \end{array}\right],\; \; b=\left[\begin{array}{c} {\begin{array}{c} {0} \\ {0} \end{array}} \\ {\begin{array}{c} {\vdots } \\ {1} \end{array}} \end{array}\right]\]

Let\(n\left(s\right)=b_0s^m+b_1s^{m-1}+\dots +b_m\) representar el polinomio numerador, donde\(m=n-1\) se asume; entonces, la matriz de salida se forma como:\[c^T=\left[b_0\quad b_1\quad \dots \quad b_m\right]\]

En la estructura de forma controlador anterior, los coeficientes del polinomio característico aparecen en orden inverso en la última fila de la matriz del sistema, mientras que la matriz de salida contiene los coeficientes del polinomio numerador.

Por lo tanto, dada una función de transferencia adecuada\(G(s)\), el formulario del controlador puede escribirse por inspección como se muestra en el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\)

Un sistema masa-resorte-amortiguador se describe mediante el modelo de función de transferencia:\(G\left(s\right)=\frac{y\left(s\right)}{u(s)}=\frac{1}{s^2+2s+2}\).

Su modelo de variable de estado de forma de controlador se da como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-2} & {-2} \end{array}\right]\, \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]\, u,\, \, \, y=\left[\begin{array}{cc} {1} & {0} \end{array}\right]\, \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]\]

Estructura de formulario de controlador alternativo

Las salidas del integrador en el diagrama de simulación se pueden numerar alternativamente de izquierda a derecha; esto reordena las variables de estado por lo que los coeficientes del polinomio característico aparecen en la primera fila de la matriz. Para el modelo de tercer orden presentado en la Fig. 8.3.3, las ecuaciones resultantes se dan como:

\[{\dot{x}}_3=-a_1 x_1 - a_2 x_2 - a_3 x_3+u,\\ {\dot{x}}_2=x_1 \\ {\dot{x}}_3=x_2 \]

La forma alternativa del controlador se obtiene usando el comando 'ss' después de definir una función de transferencia en MATLAB Control Systems Toolbox.

Ejemplo\(\PageIndex{2}\)

Un sistema masa-resorte-amortiguador se describe mediante la siguiente función de transferencia:\(G\left(s\right)=\frac{y\left(s\right)}{u(s)}=\frac{1}{s^2+2s+2}\). El modelo de variable de estado de forma del controlador se da como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]=\left[\begin{array}{cc} {-2} & {-2} \\ {1} & {0} \end{array}\right]\, \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]+\left[\begin{array}{c} {1} \\ {0} \end{array}\right]\, u,\, \, \, y=\left[\begin{array}{cc} {0} & {1} \end{array}\right]\, \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]\]

Las variables de estado se numeran en orden inverso. Por lo tanto,\(x_1\) representa la velocidad y\(x_2\) la posición de la masa inercial.

Realización Dual (Observer Form)

Supongamos que una realización de variable de estado del modelo de función de transferencia se da como:

\[\dot{x}(t)=Ax(t)+bu(t), \;\;y(t)=c^{T} x(t)\]

Su realización dual se define por el siguiente modelo de variables de estado:

\[\dot{z}(t)=A^{T} z(t)+cu(t),\;\; y(t)=b^{T} z(t)\]

Tanto el modelo original como el modelo dual comparten la misma función de transferencia escalar, es decir,

\[G(s)=c^{T} (sI-A)^{-1} b=b^T{\left(sI-A^T\right)}^{-1}c=G^T\left(s\right)\]

Cuando el modelo de variable de estado original está en forma de controlador, su dual aparece en la 'forma de observador', llamado así por su uso en el diseño de observadores estatales.

En MATLAB Control Systems Toolbox, se utiliza el comando 'canon' con la opción 'companion' para obtener la realización de la forma del observador.

Ejemplo\(\PageIndex{3}\)

Un sistema masa-resorte-amortiguador se describe mediante la siguiente función de transferencia:\(G\left(s\right)=\frac{y\left(s\right)}{u(s)}=\frac{1}{s^2+2s+2}\). Su modelo de forma controlador se derivó en el Ejemplo 8.3.1. El modelo de variable de estado de forma de observador alternativo se da como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]=\left[\begin{array}{cc} {0} & {-2} \\ {1} & {-2} \end{array}\right]\, \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right]+\left[\begin{array}{c} {1} \\ {0} \end{array}\right]\, u,\, \, \, y=\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \end{array}\right].\]

A partir de la ecuación de salida, la variable de estado\(x_2\) representa la posición de la masa inercial. A partir de la primera ecuación de estado\({\dot{x}}_1=-2x_2+u\),, la variable\(x_1\) incluye una integral de posición.

Realización Modal

Una realización modal tiene una estructura diagonal de\(1\times 1\) bloques que consiste en\(2\times 2\) bloques que contienen valores propios reales y complejos. Se utiliza una PFE de la función de transferencia para obtener factores de primer y segundo orden en el modelo de función de transferencia.

El denominador de un factor de segundo orden, expresado como\((s+\sigma )^{2} +\omega ^{2}\), puede realizarse como un\(2\times 2\) bloque que contiene las partes real e imaginaria del valor propio como:\(A_{i} =\left[\begin{array}{cc} {\sigma } & {\omega } \\ {-\omega } & {\sigma } \end{array}\right]\). Alternativamente, se puede realizar un factor de segundo orden en forma de serie, como se ilustra en el siguiente ejemplo.

En MATLAB Control Systems Toolbox, se obtiene una realización modal usando el comando 'canon' con la opción 'modal'.

Ejemplo\(\PageIndex{4}\)

Considere el siguiente modelo de tercer orden con un polo real y dos polos complejos:

\[G(s)=\frac{2(s^{2} +s+1)}{(s+2)(s^{2} +2s+2)} =\frac{3}{s+2} -\frac{s+2}{(s^{2} +2s+2)}\]

Su realización modal contiene una matriz diagonal de bloques con\(1\times 1\) y\(2\times 2\) bloques.

Una realización en serie del término de segundo orden da como resultado la siguiente realización modal:

\[\frac{d}{dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]=\left[\begin{array}{ccc} {-2} & {0} & {0} \\ {0} & {0} & {1} \\ {0} & {-2} & {-2} \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]+\left[\begin{array}{c} {1} \\ {0} \\ {1} \end{array}\right]u,\;\; y=\left[\begin{array}{ccc} {3} & {-2} & {-1} \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]\]

Alternativamente, la realización modal incluye las partes real e imaginaria del complejo valor propio. El modelo de variable de estado resultante se da como:

\[\frac{d}{dt} \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]=\left[\begin{array}{ccc} {-2} & {0} & {0} \\ {0} & {-1} & {1} \\ {0} & {-1} & {-1} \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]+\left[\begin{array}{c} {1} \\ {0} \\ {1} \end{array}\right]u,\;\; y=\left[\begin{array}{ccc} {3} & {-1} & {-1} \end{array}\right]\left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]\]

Podemos verificar que las dos realizaciones modales comparten la misma función de transferencia.

Diagonalización y desacoplamiento

Cuando el polinomio denominador en el modelo de función de transferencia tiene raíces reales y distintas, su matriz modal es una matriz diagonal con valores propios en la diagonal principal. Las ecuaciones de estado resultantes describen un conjunto de ODE desacopladas de primer orden que se pueden integrar fácilmente.

Ejemplo\(\PageIndex{5}\)

El modelo de función de transferencia de un pequeño motor de CC, dado como:\(G\left(s\right)=\frac{500}{s^2+10s+1025}\).

Un PFE de la función de transferencia da:\(\ G\left(s\right)=5.59\left[\frac{1}{s+10.28}-\frac{1}{s+99.72}\right]\).

Se obtiene una realización modal del modelo de función de transferencia como:

\[\left[\begin{array}{c} {\dot{x}_{\rm 1} } \\ {\dot{x}_{2} } \end{array}\right]=\left[\begin{array}{cc} {-99.72} & {0} \\ {0} & {-10.28} \end{array}\right]\left[\begin{array}{c} {x_{\rm 1} } \\ {x_{\rm 2} } \end{array}\right]+\left[\begin{array}{c} {1} \\ {1} \end{array}\right]V_{\rm a} , \;\;\omega =\left[\begin{array}{cc} {-5.59} & {5.59} \end{array}\right]\, \left[\begin{array}{c} {x_{\rm 1} } \\ {x_{\rm 2} } \end{array}\right]\]

Las ecuaciones de estado desacoplado y de salida que representan el modelo de motor de CC se dan como:

\[{\dot{x}}_1\left(t\right)=-99.72x_1\left(t\right)+V_a\]

\[{\dot{x}}_2\left(t\right)=-10.28x_2\left(t\right)+V_a\]

\[\omega \left(t\right)=5.59\left(x_2\left(t\right)-x_1\left(t\right)\right)\]

Podemos observar que las variables de estado en la realización diagonal representan combinaciones lineales de las variables de estado originales. Este tema se discute en la siguiente sección.