9.1: Diseño de Controlador en Espacio Sate-Space

Diseño de controlador de retroalimentación estatal

El diseño del controlador de retroalimentación de estado se refiere a la selección de ganancias de retroalimentación individuales para el conjunto completo de variables de estado. Se supone que todas las variables de estado están disponibles para su observación. El objetivo del diseño es mejorar la respuesta transitoria del sistema y reducir el error de seguimiento en estado estacionario.

\({\bf x}(t)\)Denote un vector de variables de\(n\) estado,\(u(t)\) denote una entrada escalar y\(y(t)\) denotar una salida escalar; luego el modelo de variable de estado de un sistema SISO se da como:\[\dot{\bf x}(t)={\bf Ax}(t)+{\bf b}u(t), \;\; y(t)={\bf c}^{T} {\bf x}(t)\]

donde\({\bf A}\) es una matriz de\(n\times n\) sistema,\({\bf b}\) es un vector de\(n\times 1\) columna y\({\bf c}^{T}\) es un vector de\(1\times n\) fila. El modelo de variable de estado anterior representa una función de transferencia de entrada-salida estrictamente apropiada.

El diseño del controlador en el espacio de estado implica la selección del vector de ganancia de retroalimentación adecuado\({\bf k}^T\),, que imparte las características de estabilidad y rendimiento deseadas al sistema de bucle cerrado.

Diseño de colocación de postes

El diseño de colocación de polos se refiere a la selección del vector de ganancia de retroalimentación que coloca los polos del polinomio característico en las ubicaciones deseadas. La ley de control para el diseño de colocación de postes se expresa como:\[u(t)=-{\bf k}^{T} {\bf x}(t)+r(t),\]

donde\({\bf k}^{T} =[k_{1} ,\; \; k_{2} ,\; \ldots ,k_{n} ]\) es un vector de ganancias de\(n\) retroalimentación, uno para cada una de las variables de\(n\) estado, y\(r(t)\) es una entrada de referencia.

Una condición necesaria para la colocación de polos usando retroalimentación de estado es que el par\(\left({\bf A,\,b}\right)\) es controlable, es decir, su matriz de controlabilidad\({\bf M}_{\rm C}\),, es de rango completo, donde\({\bf M}_{\rm C} =[{\bf b,\; Ab,\;\ldots ,\;A}^{n-1} {\bf b}]\).

Al incluir la ley de control en las ecuaciones de estado, el sistema de bucle cerrado se da como:

\[\dot{\bf x}(t)=({\bf A-bk}^{T}){\bf x}(t)+{\bf b}r(t)\]

El problema de diseño, entonces, es seleccionar el vector de ganancia de retroalimentación\({\bf k}^T\) que multiplica el vector de estado\({\bf x}(t)\), de manera que la matriz del sistema de bucle cerrado\({\bf A-bk}^{T}\) tenga polinomio característico que se alinee con un polinomio deseado, es decir,

\[\left|s{\bf I-A+bk}^{T} \right|=\Delta _{\rm des} (s)\]

La ecuación anterior relaciona polinomios de orden dos\(n\); al igualar los coeficientes polinomiales en ambos lados de la ecuación, obtenemos ecuaciones\(n\) lineales que pueden resolverse para las ganancias de\(n\) retroalimentación:\(k_{i} ,\; i=1,\ldots ,n\).

El polinomio característico deseado para el diseño de colocación de polos se selecciona con ubicaciones de raíz que cumplan con los criterios de rendimiento en el dominio del tiempo.

Sistema de circuito cerrado

El modelo de sistema de bucle cerrado se da como:\[\dot{\bf x}(t)={\bf A}_{\rm cl}{\bf x}(t)+{\bf b}r(t)\]

donde\({\bf A}_{\rm cl} =({\bf A-bk}^{T})\). Suponiendo estabilidad de bucle cerrado, para una entrada constante\(r(t)=r_{\rm ss}\), la respuesta de estado estacionario,\({\bf x}_{\rm ss}\), obedece:

\[0 ={\bf A}_{\rm cl} {\bf x}_{ss} +{\bf b} r_{ss} ,\;\; y_{\rm ss} ={\bf c}^T {\bf x}_{ss} \]

De ahí,\(y_{\rm ss}={\bf c}^T\,{\bf A}_{\rm cl}^{-1}\,{\bf b}\,r_{\rm ss}\).

Ejemplo\(\PageIndex{1}\)

Las ecuaciones de estado y salida para un modelo de motor de CC se dan como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right] \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a , \;\;\omega =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right].\]

El modelo motor tiene un polinomio denominador\(\Delta (s)=s^{2} +110s+1025\); sus raíces se localizan en\(s_{1,2} =-10.28,\; -99.72\) que son recíprocas de las constantes de tiempo motoras\((\tau _\rm e \cong 10\; \rm msec,\; \tau _\rm m \cong 100\; \rm msec)\).

Supongamos que las especificaciones de diseño requieren que la respuesta de bucle cerrado tenga una constante de tiempo de\(20ms\).

Para reducir las constantes de tiempo a\(20\; \rm msec\), podemos optar por colocar los polos de bucle cerrado en\(-50\),\(-100\). Entonces, el polinomio característico deseado se da como:\(\Delta _{\rm des} (s)=s^{2} +150s+5000\).

Podemos suponer\(r=0\), por lo que la ley de control se da como:\(V_a =-k^{T} x\), dónde\(k^{T} =[k_{1} ,\;k_{2} ]\).

Con la inclusión de retroalimentación de estado, la matriz del sistema de bucle cerrado se da como:

\[A-bk^{T} =\left[\begin{array}{cc} {-100(1+k_{1} )} & {-5(1+20k_{2})} \\ {5} & {-10} \end{array}\right]\]

El polinomio característico de bucle cerrado se da como:

\[\left|sI-A+bk^{T} \right|=(s+10)\left[s+100(1+k_{1} )\right]+25(1+20k_{2} ).\]

Al comparar los coeficientes de los dos polinomios, obtenemos las ganancias de retroalimentación:\(k_{1} =0.4,k_{2} =7.15\). La ley de control resultante se da como:

\[V_a\left(t\right)=-0.4\ i_a\left(t\right)-7.15\ \omega (t)\]

La matriz del sistema de circuito cerrado se da como:\(\left[\begin{array}{cc} {-140} & {-20} \\ {5} & {-10} \end{array}\right]\).

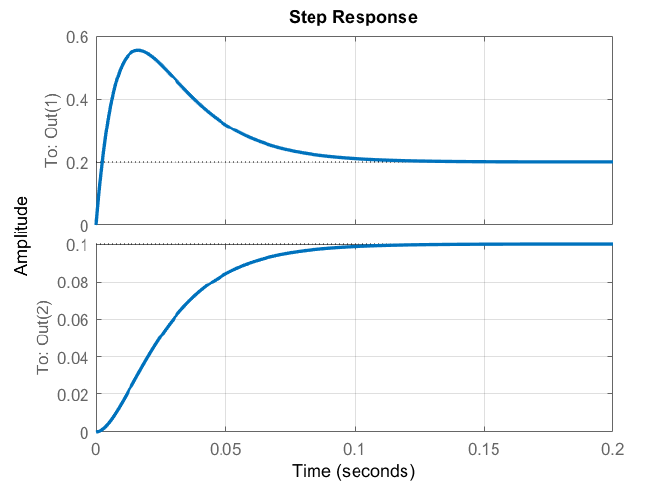
La respuesta del sistema de estado estacionario se da como:\(y_{\rm ss}=0.1r_{\rm ss}\).

La respuesta escalonada del sistema de bucle cerrado se representa en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La respuesta escalonada del motor de CC con controlador de colocación de polos: corriente de armadura (arriba); velocidad del motor (abajo).

 

Colocación de postes en forma de controlador

El diseño de colocación de postes se facilita si el modelo del sistema está en forma de controlador (Sección 8.3.1). En la estructura de forma controlador, los coeficientes del polinomio característico aparecen en orden inverso en la última fila de la\(A\) matriz.

\[A=\left[\begin{array}{cc} {\begin{array}{cc} {0\; \; \; \; \; \; \; } & {1} \\ {0\; \; \; \; \; \; \; } & {0} \end{array}} & {\begin{array}{cc} {0\; \; \; } & {\ldots } \\ {1\; \; \; } & {\ldots } \end{array}} \\ {\begin{array}{cc} {\; \; \; \vdots } & {\vdots } \\ {-a_{n} } & {-a_{n-1} } \end{array}} & {\begin{array}{cc} {\ddots } & {1} \\ {\ldots } & {-a_{1} } \end{array}} \end{array}\right],\quad b=\left[\begin{array}{c} {\begin{array}{c} {0} \\ {0} \end{array}} \\ {\begin{array}{c} {\vdots } \\ {1} \end{array}} \end{array}\right].\]

Luego, usando retroalimentación de estado completo\(u=-k^{T} x+r\), la matriz del sistema de bucle cerrado se da como:

\[A-bk^{T} =\left[\begin{array}{cc} {\begin{array}{cc} {0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; } & {1} \\ {0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; } & {0} \end{array}} & {\begin{array}{cc} {0\; \; \; \; \; \; \; } & {\ldots } \\ {1\; \; \; \; \; \; \; } & {\ldots } \end{array}} \\ {\begin{array}{cc} {\; \; \; \vdots } & {\; \; \; \vdots } \\ {-a_{n} -k_{1} } & {-a_{n-1} -k_{n-1} } \end{array}} & {\begin{array}{cc} {\ddots } & {1} \\ {\ldots } & {-a_{1} -k_{n} } \end{array}} \end{array}\right].\]

El polinomio característico de bucle cerrado se puede escribir por inspección, y se da como:

\[\Delta (s)=s^{n} +(a_{1} +k_{n} )s^{n-1} +\ldots +a_{n} +k_{1}\]

Deje que el polinomio característico deseado se defina como:

\[\Delta _{\rm des} (s)=s^{n} +\bar{a}_{1} s^{n-1} +\ldots +\bar{a}_{n-1} s+\bar{a}_{n} .\]

Al comparar los coeficientes, las ganancias de retroalimentación deseadas se calculan como:

\[k_{1} =\bar{a}_{n} -a_{n} ,\; \, \, k_{2} =\bar{a}_{n-1} -a_{n-1} ,\, \, \ldots \, \, ,\; \, \; k_{n} =\bar{a}_{1} -a_{1} .\]

Dado que las variables de estado en la forma del controlador incluyen la salida del sistema y sus derivadas, la colocación de polos usando retroalimentación de estado es una generalización de controladores de derivativo proporcional (PD) y retroalimentación de velocidad.

Ejemplo\(\PageIndex{2}\)

El modelo de variable de estado de una masa-resorte-amortiguador se da como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x} \\ {v} \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-10} & {-1} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]f, \;\; x=\left[\begin{array}{cc} {1} & {0} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right].\]

Supongamos que las especificaciones de diseño requieren elevar la amortiguación a\(\zeta =0.6\).

Dado que el modelo del sistema está en forma de controlador, su polinomio característico puede escribirse por inspección, y se da como:\(\Delta (s)=s^{2} +s+10\).

Para mejorar la amortiguación, se selecciona un polinomio característico deseado como:\(\Delta _{\rm des} (s)=s^{2} +4s+10\).

Las ganancias de retroalimentación deseadas se pueden escribir por inspección, y se dan como:\(k^T =[0\; \; 3]\).

Colocación de postes usando Bass-Gura Formula

La fórmula Bass-Gura describe una expresión simple para calcular las ganancias del controlador de retroalimentación de estado a partir de los coeficientes de los polinomios característicos de bucle cerrado disponibles y deseados. Para continuar, deje que el modelo de variable de estado se dé como:

\[\dot{x}(t)=Ax(t)+bu(t), \;\; y(t)=c^{T} x(t)\]

Suponiendo que\(\left(A,b\right)\) el par es controlable, su matriz de controlabilidad se da como:\(M_{\rm C }=[b,\; Ab,\; \ldots, \;A^{n-1} b]\).

El modelo se transforma en forma de controlador mediante una transformación lineal\(z=Px\); el modelo transformado se describe como:

\[\dot{z}(t)=A_{\rm CF} z(t)+b_{\rm CF} u(t), \;\; y(t)=c_{\rm CF}^{T} z(t)\]

La matriz de controlabilidad de la representación de forma del controlador se da como:\(M_{\rm CF} =[b_{\rm CF} ,\; A_{\rm CF} b_{\rm CF} ,\ldots ,\; A_{\rm CF} {}^{n-1} b_{\rm CF} ].\) La matriz comprende los coeficientes del polinomio característico\(\mathit{\Delta}\left(s\right)=\left|sI-A\right|\), y puede escribirse por inspección.

La matriz de transformación lineal requerida se obtiene de la siguiente relación:

\[P^{-1} =M_{\rm C} M_{\rm CF}^{-1} ,\;\; P=M_{\rm CF} M_{\rm C}^{-1} .\]

La ley estatal de control de retroalimentación en la forma del controlador se define como:

\[u=-k_{\rm CF} {}^{T} z(t)=-k_{\rm CF} {}^{T} Px(t).\]

En términos de coeficientes polinomiales, las ganancias del controlador se dan como:\(k_{\rm CF} {}^{T} =\left[\begin{array}{cccc} {\bar{a}_{n} -a_{n} } & {\bar{a}_{n-1} -a_{n-1} } & {\cdots } & {\bar{a}_{1} -a_{1} } \end{array}\right]\).

Las ganancias del controlador para el modelo de variable de estado original se obtienen como:\(k^{T} =k_{\rm CF} {}^{T} P\).

Por lo tanto, la fórmula de Bass-Gura se obtiene como:

\[k^{T} =\left[\begin{array}{cccc} {\bar{a}_{n} -a_{n} } & {\bar{a}_{n-1} -a_{n-1} } & {\cdots } & {\bar{a}_{1} -a_{1} } \end{array}\right]\, M_{\rm CF} M_{\rm C}^{-1}\]

Ejemplo\(\PageIndex{3}\)

Las ecuaciones de estado para un modelo de motor de CC se dan como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a\]

Supongamos que las especificaciones de diseño requieren una constante de tiempo de\(20ms\).

El polinomio característico del modelo es:\(\left|sI-A\right|=s^{2} +110s+1025.\)

La matriz de controlabilidad del modelo se forma como:\(M_\rm C =[b,\; Ab]=\left[\begin{array}{cc} {100} & {-10^{4} } \\ {0} & {500} \end{array}\right]\).

La representación del formulario controlador para el modelo se desarrolla como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x_1} \\ {x_{2} } \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-1025} & {-110} \end{array}\right]\left[\begin{array}{c} {x_1 } \\ {x_{2} } \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]V_a\]

La matriz de controlabilidad para la representación del formulario del controlador es:\(M_{\rm CF} =\left[\begin{array}{cc} {0} & {1} \\ {1} & {-110} \end{array}\right]\).

Supongamos que el polinomio característico deseado se selecciona como:\(\Delta _{\rm des} (s)=s^{2} +150s+5000\).

Las ganancias de retroalimentación para la representación del formulario del controlador se obtienen como:\(k_{\rm CF} {}^{T} =\left[\begin{array}{cc} {3975} & {40} \end{array}\right]\).

Usando la fórmula Bass-Gura, las ganancias del controlador de retroalimentación de estado para el modelo de motor de CC se calculan como:\(k^{T} =k_{\rm CF} {}^{T} \, M_{\rm CF} M_{\rm C}^{-1} =\left[\begin{array}{cc} {0.4} & {7.15} \end{array}\right]\).

La ley de control de retroalimentación estatal resultante se da como:\(V_{a} =-0.4i_{a} -7.15\omega\).

Colocación de postes usando la fórmula de Ackermann

La fórmula de Ackermann es, asimismo, una expresión simple para calcular las ganancias del controlador de retroalimentación de estado para la colocación de polos. Para desarrollar la fórmula, deje que un modelo de variable de estado\(n\) -dimensional se dé como:

\[\dot{x}(t)=Ax(t)+bu(t)\]

La matriz de controlabilidad del modelo se forma como:\(M_{\rm C} =[b,\; Ab,\;\ldots ,\;A^{n-1} b].\)

Supongamos que un polinomio característico deseado se da como:\(\Delta _{\rm des} (s)=s^{n} +\bar{a}_{1} s^{n-1} +\ldots +\bar{a}_{n-1} s+\bar{a}_{n} \).

A continuación, evaluamos el siguiente polinomio matricial que involucra a la matriz del sistema:

\[\Delta _{\rm des} (A)=A^{n} +\bar{a}_{1} A^{n-1} +\ldots +\bar{a}_{n-1} A+\bar{a}_{n} I.\]

donde\(I\) denota una matriz de\(n\times n\) identidad. Las ganancias del controlador de retroalimentación de estado se obtienen a partir de la siguiente fórmula de Ackermann:

\[k^{T} =\left[\begin{array}{cccc} {0} & {\cdots } & {0} & {1} \end{array}\right]\, M_{\rm C} {}^{-1} \Delta _{\rm des} (A)\]

Ejemplo\(\PageIndex{4}\)

Las ecuaciones de estado para un modelo de motor de CC se dan como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a\]

Que se dé el polinomio característico deseado como:\(\Delta _{\rm des} (s)=s^{2} +150s+5000\).

La matriz de controlabilidad para el modelo se calcula como:\(M_{\rm C} =[b,\; Ab]=\left[\begin{array}{cc} {100} & {-10^{4} } \\ {0} & {500} \end{array}\right]\).

El polinomio matriz utilizado en la fórmula se evalúa como:\(\Delta _{\rm des} (A)=\left[\begin{array}{cc} {-25} & {-200} \\ {200} & {3575} \end{array}\right]\).

Usando la fórmula de Ackermann, el controlador de colocación de polos se calcula como:\(k^{T} =\left[\begin{array}{cc} {0.4} & {7.15} \end{array}\right]\).

La ley de control de retroalimentación estatal resultante se da como:\(V_{a} =-0.4i_{a} -7.15\omega\).

MATLAB Control System Toolbox incluye el comando 'place' que utiliza la fórmula de Ackermann para el diseño de colocación de postes. El comando se invoca ingresando la matriz del sistema, el vector de entrada y un vector de raíces deseadas del polinomio característico. La función devuelve el vector de ganancia de retroalimentación que coloca los valores propios de\(A-bk^{T}\), en las ubicaciones de raíz deseadas.

Colocación de polos usando la ecuación de Sylvester

La ecuación de Sylvester en álgebra lineal es una ecuación matricial\(AX+XB=C\), dada como:, donde\(A\) y\(B\) son matrices cuadradas de dimensiones no necesariamente iguales, y\(C\) es una matriz de dimensiones apropiadas. La matriz de solución\(X\) es de la misma dimensión que\(C\).

Para aplicar la ecuación de Sylvester para el diseño de colocación de polos, se dé un modelo de variable de estado\(n\) -dimensional como: Se supone que\[\dot{x}(t)=Ax(t)+bu(t)\] el par\((A,b)\) es controlable.

Let\(A-bk^T\) representa la matriz del sistema de bucle cerrado; supongamos que una transformada de similitud diagonalizante se define como:\[X^{-1}\left(A-bk^T\right)X=\mathit{\Lambda}\] La matriz\(\mathit{\Lambda}\) es diagonal y contiene los valores propios deseados; puede asumirse en forma modal para valores propios complejos.

Dejar\(k^TX=g^T\); entonces, la ecución de Sylvester se formula como: Existe\[AX-X\mathit{\Lambda}=bg^T\] una solución única\(X\) a la ecuación de Sylvester si los valores propios de\(A\) y\(\mathit{\Lambda}\) son distintos, es decir,\({\lambda }_i\left(A\right)-{\lambda }_j\left(\mathit{\Lambda}\right)\neq 0\).

El procedimiento de diseño para la colocación de postes usando la ecuación de Sylvester se da de la siguiente manera:

1. Elija una matriz\(\mathit{\Lambda}\) de valores propios deseados en forma modal. Elija cualquiera\(g^T\) y resuelva\(AX-X\mathit{\Lambda}=bg^T\) para\(X\).
2. Recuperar el vector de ganancia de retroalimentación de\(k^T=g^TX^{-1}\). Si no\(X\) es invertible, elija una diferente\(g^T\) y repita el procedimiento.

Ejemplo\(\PageIndex{5}\)

La ecuación de estado para el modelo masa-resorte-amortiguador se describe como:\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x} \\ {v} \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-10} & {-1} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]f\]

Dejar que se seleccione un polinomio característico deseado como:\(\Delta _{\rm des} (s)=s^{2} +4s+10\); entonces, la matriz modal de los autovalores deseados es:\(\Lambda =\left[\begin{array}{cc} {-2} & {\sqrt{6} } \\ {-\sqrt{6} } & {-2} \end{array}\right]\).

Vamos\(g^{T} =[1\; \; 0]\); entonces,\(bg^{T} =\left[\begin{array}{cc} {0} & {0} \\ {1} & {0} \end{array}\right]\). La solución a la ecuación de Sylvester se obtiene como:\(X=\left[\begin{array}{cc} {-0.067} & {-0.082} \\ {0.333} & {0.0} \end{array}\right]\).

Las ganancias del controlador de retroalimentación se calculan como:\(k^{T} =[0\; \; 3]\).