9.2: Seguimiento con controlador Feedforward

Diseño de seguimiento con controlador Feedforward

Un sistema de rastreo está diseñado para alcanzar asintóticamente y mantener un error de estado estacionario cero con respecto a una entrada de referencia,\(r\left(t\right)\). Esto se puede lograr usando\(r\left(t\right)\) para cancelar\(e\left(t\right)\) en el estado estacionario.

La señal de referencia se puede usar con una ganancia de avance para cancelar la señal de error. Hacia este fin, dejemos que el modelo de variable de estado se dé como:\[\dot{x}(t)=Ax(t)+bu(t), \;\;y(t)=c^{T} x(t)\]

La ley asintótica de control de rastreo se define como:\[u(t)=-k^{T} x(t)+k_{r} r(t)\] donde\(k_{r}\) es una ganancia escalar. El sistema de bucle cerrado se forma como:\[\dot{x}(t)=\left(A-bk^{T} \right)x(t)+bk_{r} r(t), y(t)=c^{T} x(t)\]

Suponiendo que el sistema de bucle cerrado es estable, let\(\dot{x}(t)=0\); los valores de estado estacionario de las variables de estado se obtienen como:\[x_{ss} =-\left(A-bk^{T} \right)^{-1} bk_{r} r_{ss} .\]

La salida de estado estacionario se da como:\[y_{ss} =-c^{T} \left(A-bk^{T} \right)^{-1} b\, k_{r} r_{ss}\]

Defina la función de transferencia de bucle cerrado:\[T(s)=c^{T} \left(sI-A+bk^{T} \right)^{-1} b\]

Entonces, la salida en estado estacionario es:\(y_{ss} =T(0)k_{r} r_{ss}\).

Con el fin de asegurar\(y_{ss} =r_{ss}\), podemos elegir,\(k_{r} =T(0)^{-1}\).

Además, si\(y=x_{1}\), entonces se\(k_{r}\) puede seleccionar como\(k_{r} =k_{1}\), para asegurar\(r-y=0\) en el estado estacionario.

Ejemplo\(\PageIndex{1}\)

Las ecuaciones de estado y salida para un modelo de motor de CC se dan como:\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a,\;\; \omega =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_a} \\ {\omega } \end{array}\right].\]

Un controlador de colocación de polos para el modelo de motor de CC se diseñó previamente como:\(V_{a} =-0.4i_{a} -7.15\omega\). Se revisa la ley de control para incluir una ganancia de feedforward:\(V_{a} =-0.4i_{a} -7.15\omega +k_{r} r\), donde queremos elegir\(k_r\) por cero error de estado estacionario.

Al incluir el controlador, el modelo de sistema de bucle cerrado se da como:\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-140} & {-720} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]k_{r} r\]

Las variables de estado asumen los siguientes valores en estado estacionario:\(\left[\begin{array}{c} {i_{a,ss} } \\ {\omega _{ss} } \end{array}\right]=\left[\begin{array}{c} {0.2} \\ {0.1} \end{array}\right]k_{r} r_{ss}\).

El valor de estado estacionario de la salida se da como:\(y_{ss} =0.1k_{r} r_{ss}\). Entonces, podemos elegir\(k_{r} =10\) por cero error de estado estacionario.

La ley de conrol resultante se da como:\(V_{a} =-0.4i_{a} -7.15\omega +10r\).

En la Fig. 9.2.1 se muestra una gráfica de la respuesta del motor con compensación de avance. Como era de esperar, la velocidad del motor se aproxima asintóticamente a la unidad en el estado estacionario.

Figura\(\PageIndex{1}\): La respuesta escalonada del motor de CC con controlador de colocación de polos y compensación de avance: corriente de armadura (arriba); velocidad del motor (abajo).

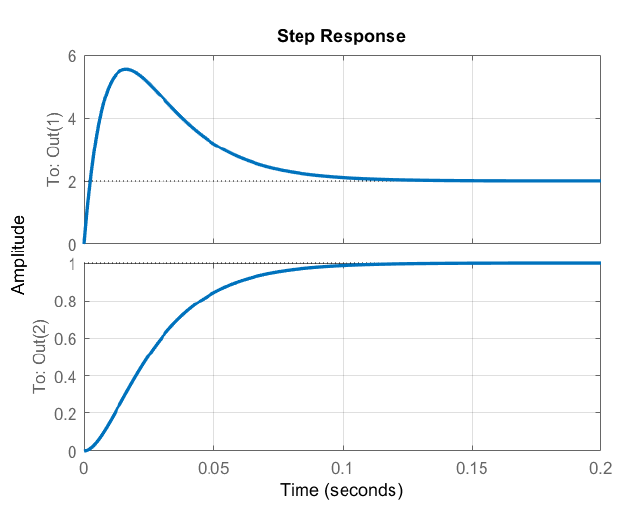
Ejemplo\(\PageIndex{2}\)

El modelo de variable de estado de una masa-resorte-amortiguador se da como:\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x} \\ {v} \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-10} & {-1} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right]+\left[\begin{array}{c} {0} \\ {1} \end{array}\right]f, \;\;x=\left[\begin{array}{cc} {1} & {0} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right]\]

Un controlador de colocación de postes para el modelo fue diseñado previamente como:\(f=-3v\).

La ley de control se modifica para incluir una ganancia de feedforward como:\(f=-3v+k_{r} r.\)

El modelo de sistema de bucle cerrado se da como:\(\frac{\rm d}{\rm dt} \left[\begin{array}{c} {x} \\ {v} \end{array}\right]=\left[\begin{array}{cc} {0} & {1} \\ {-10} & {-4} \end{array}\right]\left[\begin{array}{c} {x} \\ {v} \end{array}\right]+k_{r} r\).

La salida en estado estacionario es:\(y_{ss} =0.1k_{r} r_{ss}\). Por lo tanto, podemos elegir\(k_{r} =10\) un seguimiento sin errores. La ley de control resultante se da como:\(f=-3v+10\, r.\)