6.1: Introducción - Señales, Sistemas y Modelos

Un sistema puede ser pensado como algo que impone restricciones a -o impone relaciones entre- un conjunto de variables. Este punto de vista de “sistema como restricciones” es muy general y poderoso. Más restringida, pero aún muy útil y común, es la visión de un sistema como un mapeo de un conjunto de variables de entrada a un conjunto de variables de salida; un mapeo es evidentemente una forma de restricción muy particular.

Un modelo (conductual) enumera las variables de interés (las variables "manifiesto") y las restricciones que deben satisfacer. Cualquier combinación de variables que satisfaga las restricciones es posible o permitida, y se denomina un comportamiento del modelo.

Para facilitar la especificación de las restricciones, se pueden introducir variables auxiliares (” latentes “). Uno podría entonces distinguir entre el comportamiento manifiesto, el comportamiento latente y el comportamiento completo (tanto manifiesto como latente).

Para un modelo dinámico, las “variables” a las que se hace referencia anteriormente son en realidad señales que evolucionan en función del tiempo (y/o una función de otras variables independientes, por ejemplo, el espacio). Primero necesitamos especificar un eje de tiempo\(\mathbb{T}\) (discreto, continuo, infinito, semi-infinito.) y un espacio de señal\(\mathbb{W}\), es decir, el espacio de valores en los que viven las señales en cada instante de tiempo. Luego se completa un modelo dinámico para un conjunto de señales\(\left\{w_{i}(t)\right\}\) enumerando las restricciones que\(w_{i}(t)\) debe satisfacer. Cualquier combinación\ (w (t) =\ left [\ begin {array} {lll}
w_ {1} (t), &\ cdots, & w_ {\ ell} (t)
\ end {array}\ right]\) de señales que satisfaga las restricciones es un comportamiento del modelo,\(w(t) \in \mathbb{B}\), donde\(\mathbb{B}\) denota el comportamiento.

Presentamos ahora algunos ejemplos de modelos dinámicos, para destacar diversas representaciones de modelos posibles

Ejemplo 6.1 (Circuito)

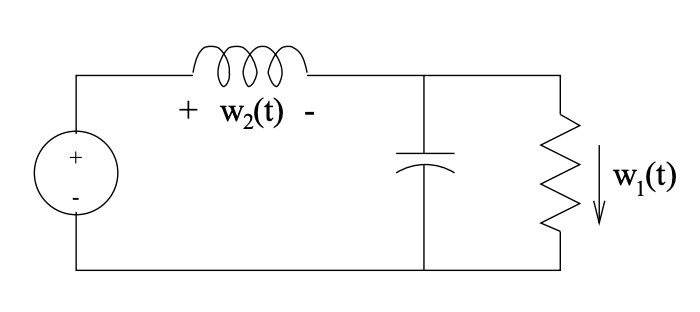
Supongamos que las señales (variables) de interés -las señales de manifiesto- en el diagrama de circuito anterior son\(w_{1}(t)\),\(w_{2}(t)\) y\(w_{3}(t)\) para\(t \geq 0\), entonces el espacio de señal\(\mathbb{W}\) es\(\mathbb{R}^{3}\) y el eje de tiempo\(\mathbb{T}\) es\(\mathbb{R}^{+}\) (es decir, el intervalo\([0, \infty]\)). Escogiendo todos los demás voltajes y corrientes de componentes como señales latentes, podemos escribir las restricciones que definen el modelo como:

\[$\left\{\begin{array}{l}2 \text { Kirchhoff's voltage law }(\mathrm{KVL}) \text { equations } \\ 2 \text { Kirchhoff's current law (KCL) equations } \\ 4 \text { defining equations for the components }\end{array}\right.$\nonumber\]

Cualquier conjunto de señales manifiestas y latentes que simultáneamente satisfaga (o resuelva) las ecuaciones de restricción anteriores constituye un comportamiento, y el comportamiento\(\mathbb{B}\) del modelo es el espacio de todas esas soluciones.

El mismo comportamiento puede ser descrito de manera equivalente por un modelo escrito íntegramente en términos de las variables manifiestas, eliminando todas las demás variables en las ecuaciones anteriores para obtener

\[0=\frac{w_{1}}{R}+C \dot{w}_{1}-w_{2}\ \tag{6.1}\]

\[0=-w_{3}+L \dot{w}_{2}+w_{1}\ \tag{6.2}\]

Aún más reducción a una única ecuación diferencial de segundo orden es posible, tomando la derivada de una de estas ecuaciones y eliminando una variable.

Ejemplo 6.2 (Sistema Masa-Muelle)

Un objeto de masa\(M\) se mueve sobre una corredera horizontal sin fricción, y se une a un extremo de la misma por un resorte lineal con constante de resorte\(k\). Se\(u(t)\) aplica una fuerza horizontal a la masa. Supongamos que la variable\(z\) mide el cambio en la longitud del resorte a partir de su longitud natural. De la ley de Newton obtenemos el modelo

\[M \ddot{z}=-k z+u\nonumber\]

Ejemplo 6.3 (Péndulo invertido)

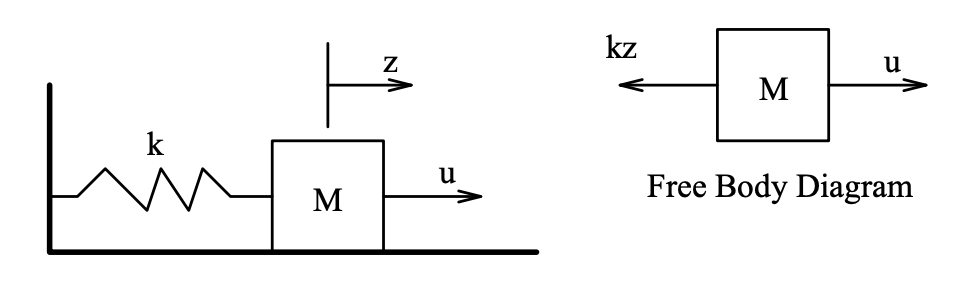
Figura\(\PageIndex{1}\): Sistema de Muelle Masivo.

Un carro de masa M se desliza sobre una pista horizontal sin fricción, y es tirado por una fuerza horizontal\(u(t)\). En el carro\(m\) se fija un péndulo invertido de masa a través de una bisagra sin fricción, como se muestra en la Figura 28.1. El centro de masa del péndulo se ubica a cierta\(l\) distancia de sus dos extremos, y el momento de inercia del péndulo alrededor de su centro de masa se denota por\(I\). El punto de soporte del péndulo está a una distancia\(s(t)\) de algún punto de referencia. El ángulo\(\theta(t)\) es el ángulo que hace el péndulo con respecto al eje vertical. La fuerza vertical ejercida por el carro sobre la base del péndulo se denota por\(P\), y la fuerza horizontal por\(N\). Lo que queremos modelar son las limitaciones que rigen las señales (manifiestas)\(u(t)\),\(s(t)\) y\(\theta(t)\).

Primero escribamos las ecuaciones de movimiento que resultan del diagrama de cuerpo libre del carro. Las fuerzas verticales\(P\),\(R\) y\(Mg\) equilibran. Para las fuerzas horizontales tenemos la siguiente ecuación:

\[M \ddot{s}=u-N\ \tag{6.3}\]

Del diagrama de cuerpo libre del péndulo, el equilibrio de fuerzas en la dirección hori- zontal da la ecuación

\ [\ begin {alineado}
m\ frac {d^ {2}} {d t^ {2}} (s+l\ sin (\ theta)) &=N,\ o\\
m\ izquierda (\ ddot {s} -l\ sin (\ theta) (\ punto {\ theta}) ^ {2} +l\ cos (\ theta)\ ddot {\ theta}\ derecha) &=N,\ (6.4)
\ final {alineado}\ nonumber\]

y el equilibrio de fuerzas en la dirección vertical da la ecuación

\ [\ begin {alineado}
m\ frac {d^ {2}} {d t^ {2}} (l\ cos (\ theta)) &=p-m g,\ o\\
m\ izquierda (-l\ cos (\ theta) (\ punto {\ theta}) ^ {2} -l\ sin (\ theta)\ ddot {\ theta}\ derecha) &=P-m g.\ (6.5)
\ final {alineado}\ nonumber\]

A partir de las ecuaciones (28.16) y (28.17) podemos eliminar la fuerza\(N\) para obtener

\[(M+m) \ddot{s}+m\left(l \cos (\theta) \ddot{\theta}-l \sin (\theta)(\dot{\theta})^{2}\right)=u \ \tag{6.6}\]

Al equilibrar los momentos alrededor del centro de masa, obtenemos la ecuación

\[I \ddot{\theta}=P l \sin (\theta)-N l \cos (\theta) \ \tag{6.7}\]

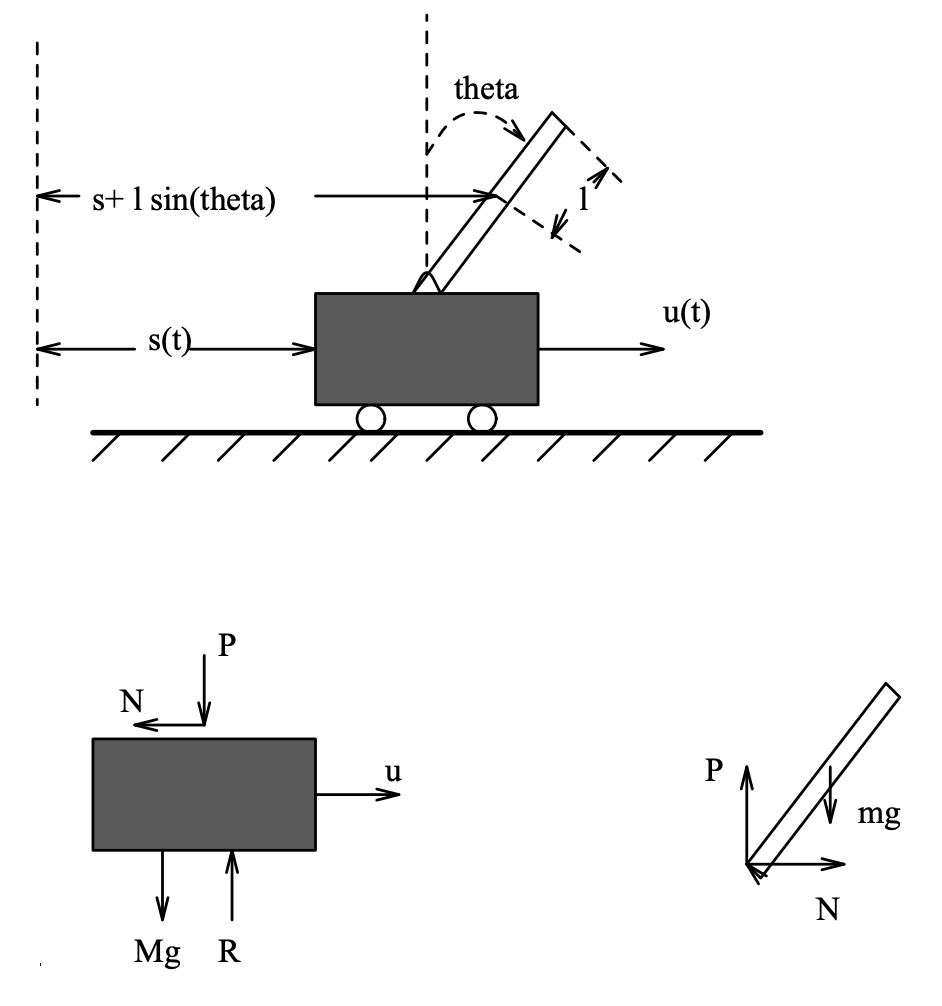
Figura\(\PageIndex{2}\): Péndulo invertido

Sustituir (28.17) y (28.18) en (28.19) nos da

\ [\ comenzar {alineado}
I\ ddot {\ theta} &=l\ izquierda (m g-m l\ cos (\ theta) (\ punto {\ theta}) ^ {2} -m l\ sin (\ theta)\ ddot {\ theta}\ derecha)\ sin (\ theta)\\
&-l\ izquierda (m\ ddot {s} -m l\ sin (\ theta) (\ punto {\ theta}) ^ {2} +m l\ cos (\ theta)\ ddot {\ theta}\ derecha)\ cos (\ theta)
\ fin {alineado} \ nonumber\]

Simplificar la expresión anterior nos da la ecuación

\[\left(I+m l^{2}\right) \ddot{\theta}=m g l \sin (\theta)-m l \ddot{s} \cos (\theta)\ \tag{6.8}\]

Las ecuaciones que componen nuestro modelo para el sistema son (28.20) y (28.21).

Podemos tener una mayor simplificación del sistema de ecuaciones eliminando el término\( \ddot{\theta}\) de la ecuación (28.20), y el término\( \ddot{s}\) de la ecuación (28.21). Definir las constantes

\ [\ begin {alineado}
\ mathcal {M} &=M+M\\
L &=\ frac {I+M l^ {2}} {m l}
\ end {alineado}\ nonumber\]

Sustituyendo\( \ddot{\theta}\) de (28.21) a (28.20), obtenemos

\[\left(1-\frac{m l}{\mathcal{M} L} \cos (\theta)^{2}\right) \ddot{s}+\frac{m l}{\mathcal{M} L} g \sin (\theta) \cos (\theta)-\frac{m l}{\mathcal{M}} \sin (\theta)(\dot{\theta})^{2}=\frac{1}{\mathcal{M}} u \ \tag{6.9}\]

Del mismo modo podemos sustituir\( \ddot{s}\) de (28.20) a (28.21) para obtener

\[\left(1-\frac{m l}{\mathcal{M} L} \cos (\theta)^{2}\right) \ddot{\theta}-\frac{g}{L} \sin (\theta)+\frac{m l}{\mathcal{M} L} \sin (\theta) \cos (\theta)(\dot{\theta})^{2}=-\frac{1}{\mathcal{M} L} \cos (\theta) u. \ \tag{6.10}\]

Ejemplo 6.4 (Modelo depredador-presa)

Si bien los ejemplos anteriores se basan físicamente, hay muchos ejemplos de modelos dinámicos que se hipotetizan sobre la base de un patrón de comportamiento. Para una ilustración clásica, considere una isla poblada principalmente por cabras y zorros. Las cabras sobreviven en la vegetación de la isla mientras que los zorros sobreviven comiendo cabras.

Para construir un modelo del crecimiento poblacional de estos dos animales que interactúan, defina:

\[N_{1}(t)= \text{number of goats at time t} \ \tag{6.11}\]

\[N_{2}(t)= \text{number of foxes at time t} \ \tag{6.12}\]

donde\(t\) se refiere al tiempo (discreto) medido en múltiplos de meses. Volterra propuso el siguiente modelo:

\[N_{1}(t+1)=a N_{1}(t)-b N_{1}(t) N_{2}(t)\ \tag{6.13}\]

\[N_{2}(t+1)=c N_{2}(t)+d N_{1}(t) N_{2}(t)\ \tag{6.14}\]

Las constantes\(a\),\(b\),\(c\) y\(d\) son todas positivas, con\(a > 1\),\(c < 1\). Si no hubiera cabras en la isla\(N_{1}(0) = 0\), entonces -según este modelo- la población de los zorros disminuiría geométricamente (es decir, como exponencial de tiempo discreto). Si no hubiera zorros en la isla, entonces la población caprina crecería geométricamente (presumiblemente hay un suministro ilimitado de vegetación, agua y espacio). Por otro lado, si ambas especies existieran en la isla, entonces la frecuencia de sus encuentros, que se modela como proporcional al producto\(N_{1}N_{2}\), determina a qué ritmo se comen las cabras y los zorros están bien alimentados. Entre las preguntas que podrían plantearse ahora están: ¿Qué tipo de características cualitativas de comportamiento están asociadas a dicho modelo y qué predicciones se derivan de este comportamiento? ¿Qué opciones de los parámetros\(a\),\(b\),\(c\), coinciden\(d\) mejor con el comportamiento observado en la práctica?

Ejemplo 6.5 (Manchado en un sistema de imágenes)

Considere un modelo que describa la relación entre un objeto bidimensional y su imagen en una película plana en una cámara. Debido a la apertura limitada, las imperfecciones de la lente y los errores de enfoque, se manchará la imagen de una fuente puntual unitaria en el origen del objeto, representada por el impulso unitario\(\delta (x, y)\) en el plano del objeto. La intensidad de la luz en la imagen puede ser modelada por alguna función\(h(x, y), x, y \in R\), por ejemplo\(h(x, y) = e^{-a(x^{2}+y^{2})}\). Un objeto\(u(x, y)\) puede ser visto como la superposición de puntos individuales distribuidos espacialmente, es decir,

\[u(x, y)=\iint_{-\infty}^{\infty} \delta(x-\lambda, y-\mu) u(\lambda, \mu) d \lambda d \mu\nonumber\]

Suponiendo que el efecto de la lente es lineal e invariante de traslación, la imagen de dicho objeto viene dada por la siguiente función de intensidad:

\[m(x, y)=\iint_{-\infty}^{\infty} h(x-\lambda, y-\mu) u(\lambda, d \mu) d \lambda d \mu\nonumber\]

Podemos ver u como la entrada a este sistema,\(m\) como la salida.