18.1: SISO Loop Shaping

El Mirador Clásico

La configuración estándar de “servo” o seguimiento del control de retroalimentación clásico se muestra en la Figura 18.1. En esta disposición, el controlador\(K\) es alimentado por una señal de error\(e\), que es la diferencia entre una referencia\(r\) y la salida medida\(y\) de la planta\(P\). La medición quizá esté corrompida por el ruido\(n\). La salida del controlador es la entrada\(u\) a la planta. Además, las perturbaciones externas pueden conducir la planta, y se representan aquí a través de la señal\(d\) agregada en la salida de la planta. En un diseño típico de control clásico, el compensador se\(K\) elegiría como el sistema de orden más bajo que asegura lo siguiente:

1. el sistema de circuito cerrado es estable;

Figura\(\PageIndex{1}\): Configuración de retroalimentación estándar con entradas de ruido, perturbación y referencia.

2. la ganancia de bucle\(P(j \omega) K(j \omega)\) tiene gran magnitud a frecuencias (frecuencias bajas, típicamente) donde se concentra la potencia de la perturbación de la planta\(d\) o entrada\(r\) de referencia.

3. la ganancia de bucle tiene pequeña magnitud a frecuencias (frecuencias altas, típicamente) donde\(n\) se concentra la potencia del ruido de medición.

La necesidad del primer requisito es clara. A continuación se explicarán los orígenes de los requisitos segundo y tercero. Para lograr simultáneamente los tres objetivos, lo más conveniente es tener un criterio de estabilidad de bucle cerrado que se establezca en términos de la ganancia de bucle (openloop), y esto es proporcionado por el criterio de estabilidad de Nyquist.

Las razones de los requisitos segundo y tercero anteriores se encuentran en las sensibilidades del sistema de circuito cerrado a las perturbaciones de la planta, las señales de referencia y el ruido de medición. Let\(S\) denotar la función de transferencia que mapea una perturbación\(d\) a la salida\(y\) en el sistema de bucle cerrado. Esto\(S\) se llama la función de sensibilidad (salida), y para la disposición en la Figura 18.1 viene dada por

\[S=(1+P K)^{-1} \ \tag{18.1}\]

Hablando informalmente por el momento, si\(|P(j \omega) K(j \omega)|\) es grande en frecuencias donde (en cierto sentido)\(d\) se concentra el poder de, entonces\(|S(j \omega)|\) será pequeño ahí, por lo que se atenúa el efecto de la perturbación en la salida. Dado que las perturbaciones de las plantas se concentran típicamente alrededor del extremo inferior del espectro de frecuencias, uno\(|P(j \omega) K(j \omega)|\) querría ser grande a bajas frecuencias. Así, el rechazo de perturbaciones es una motivación clave detrás de la especificación de baja frecuencia del control clásico sobre la ganancia de bucle.

Tenga en cuenta que (en el caso SISO)\(S\) es también la función de transferencia de\(r\) a\(e\). Si queremos\(y\) realizar un seguimiento\(r\) con buena precisión, entonces queremos una pequeña respuesta de la señal de error\(e\) a la señal de conducción\(r\). Esto nuevamente nos lleva\(|S(j \omega)|\) a pedir ser pequeños -o equivalentemente grandes-\(|P(j \omega) K(j \omega)|\) a frecuencias donde\(r\) se concentra la potencia de la señal de referencia. Afortunadamente, en muchas (si no la mayoría) aplicaciones de control, la señal de referencia va variando lentamente, por lo que este requisito nuevamente se reduce\(|P(j \omega) K(j \omega)|\) a pedir ser grande a bajas frecuencias. Por lo tanto, la precisión del seguimiento es otra motivación detrás de la especificación de baja frecuencia del control clásico sobre la ganancia de bucle.

En contraste, la motivación detrás de la especificación de alta frecuencia del control clásico es el rechazo de ruido. Let\(T\) denotar la función de transferencia que mapea la entrada de ruido\(n\) a la salida\(y\). Dada la disposición de la Figura 18.1,

\[T=P K(1+P K)^{-1} \ \tag{18.2}\]

Esto\(T\) se llama la función de sensibilidad complementaria, porque

\ (T + S = 1\\ etiqueta {18.3}\]

Tenga en cuenta que también\(T\) es la función de transferencia de\(r\) a\(y\). Si\(|P(j \omega) K(j \omega)|\) es pequeño a frecuencias donde\(n\) se concentra la potencia de entrada, entonces\(|T(j \omega)|\) será pequeño allí, por lo que se atenúa el efecto del ruido en la salida. El ruido de medición tiende a ocurrir a frecuencias más altas, por lo que para minimizar sus efectos sobre la salida, normalmente especificamos que\(|P(j \omega) K(j \omega)|\) sean pequeños a altas frecuencias. Esta restricción afortunadamente no entra en conflicto con las restricciones de baja frecuencia impuestas anteriormente por los típicos\(d\) y\(r\). Además, la restricción está bien adaptada al hecho inevitable de que la ganancia de los sistemas físicos eventualmente caerá con la frecuencia.

La imagen de la tarea de diseño de control que surge de la discusión anterior es la siguiente: Dada la planta\(P\), normalmente se necesita elegir el compensador\(K\) para obtener una magnitud de ganancia de bucle\(|P(j \omega) K(j \omega)|\) que sea grande a bajas frecuencias, “roll off” a valores bajos a altas frecuencias, y varía de tal manera que se cumple el criterio de estabilidad Nyquist. [Para el caso especial de plantas estables de bucle abierto y compensadores, la condición de estabilidad se puede afirmar en formas alternativas que son fáciles de verificar usando parcelas Bode en lugar de parcelas Nyquist, y esto puede ser más conveniente. La regla general estándar se centra en el roll-off alrededor de la frecuencia de cruce\(\omega_{c}\), definida como la frecuencia donde la magnitud de ganancia de bucle es la unidad; esta frecuencia es una medida bruta del ancho de banda de bucle cerrado. La especificación es que el roll-off de la magnitud de ganancia de bucle alrededor no\(\omega_{c}\) debe ser más pronunciada que -20dB/década. Además, se\(\omega_{c}\) debe seleccionar por debajo de las frecuencias donde la ganancia de bucle se ve afectada significativamente por cualquier ceros de medio plano derecho de la función de transferencia de bucle\(P K\); esto proporciona una indicación inicial de que los ceros de medio plano derecho pueden limitar el rendimiento de bucle cerrado alcanzable.]

Un Mirador Moderno

El reto ahora es traducir el enfoque de diseño de control clásico anterior en algo más preciso y sistemático, y más probable que tenga una extensión MIMO natural. El siguiente ejemplo señala el camino, y hace uso gratuito de las normas de señal y sistema que definimos en las Conferencias 11 y 12.

Ejemplo 18.1 (rechazo de perturbaciones de SISO y sensibilidad ponderada)

Ya hemos visto que la expresión\(y\) relacionada\(d\) en la configuración de retroalimentación SISO representada en la Figura 18.1 es

\[y=(1+P K)^{-1} d \ \tag{18.4}\]

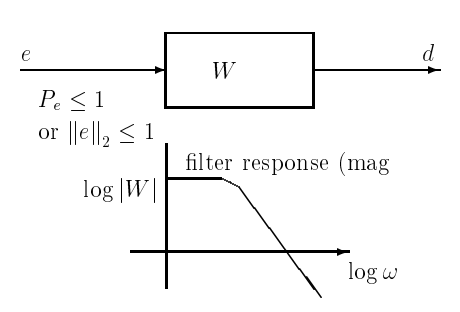
Figura\(\PageIndex{2}\): Representar la perturbación de la planta\(d\) como la salida de un filtro de conformación\(W\) cuya entrada\(e\) es una señal arbitraria de energía limitada o potencia acotada, o posiblemente ruido blanco.

Típicamente,\(d\) tiene contenido de frecuencia concentrado en el rango de baja frecuencia. Para obtener la característica de frecuencia requerida, se podría modelar\(d\) como la salida de un filtro de conformación con función de transferencia\(W\), como se muestra en la Figura 18.2, siendo la entrada\(e\) del filtro una energía acotada arbitraria o perturbación de potencia limitada (o, en ajuste estocástico, ruido blanco). Así no\(e\) tiene “coloración” espectral, y toda la coloración de\(d\) se materializa en la respuesta de frecuencia de\(W\).

Para el resto de este ejemplo, centrémonos en los modelos de energía acotada o potencia acotada para\(e\). Supongamos que nuestro objetivo ahora es\(K\) elegir minimizar el efecto de la perturbación\(d\) en la salida\(y\). De las Conferencias 11 y 12, y dado nuestro modelo para\(d\), sabemos que esto equivale a minimizar la\(\mathcal{H}_{\infty}\) ganancia de la función de transferencia de\(e\) a\(y\), porque en el caso de una potencia acotada\(e\) esta ganancia es el límite alcanzable o “apretado” en la relación de valores rms en la salida y la entrada,

\[\frac{\rho_{y}}{\rho_{e}} \leq\left\|(1+P(j \omega) K(j \omega))^{-1} W(j \omega)\right\|_{\infty}\nonumber\]

mientras que en el caso de una energía acotada\(e\) volvemos a tener el atajo apretado

\[\frac{\|y\|_{2}}{\|e\|_{2}} \leq\left\|(1+P(j \omega) K(j \omega))^{-1} W(j \omega)\right\|_{\infty}\nonumber\]

En cuanto a la función de sensibilidad,

\[S(j \omega)=(1+P(j \omega) K(j \omega))^{-1}\nonumber\]

la tarea es escoger\(K\) para minimizar la\(\mathcal{H}_{\infty}\) norma\(\|S(j \omega) W(j \omega)\|_{\infty}\).

Si

\[\|S(j \omega) W(j \omega)\|_{\infty} \leq \gamma \ \tag{18.5}\]

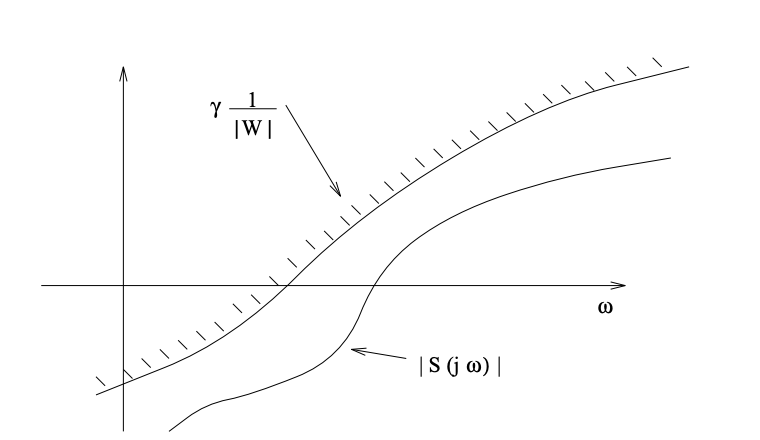
Figura\(\PageIndex{3}\): Interpretación gráfica de la función de sensibilidad estando delimitada por un recíproco escalado de la respuesta de frecuencia del filtro de ponderación.

entonces

\[|S(j \omega)||W(j \omega)| \leq \gamma, \forall \omega \ \tag{18.6}\]

Esto implica que

\[|S(j \omega)| \leq \gamma \frac{1}{|W(j \omega)|} \ \tag{18.7}\]

que nos dice que la función de sensibilidad está limitada por un recíproco escalado del filtro de ponderación. Una representación gráfica de este encuadernado se muestra en la Figura 18.3. De la Figura 18.3 podemos ver que el valor\(\gamma\) y el filtro nos\(W(j \omega)\) dan una imagen clara de la restricción en la función de sensibilidad. Esto permite a uno diseñar de manera más sistemática un controlador, ya que obtenemos directamente las características de bucle cerrado. Obsérvese también que con la\(Q\) -parametrización de\(K\), la función de sensibilidad\(S\) es afín en\(Q\), y esta forma es mucho más fácil de trabajar que la forma fraccionaria que\(S\) toma como función de\(K\).

El mayor beneficio de la formulación en el ejemplo anterior es que una versión MIMO de la misma es bastante inmediata, como vemos en la siguiente sección.