20.7: Análisis de estabilidad y robustez

A continuación, presentamos algunos ejemplos para ilustrar el uso del teorema de pequeña ganancia en el análisis de robustez de estabilidad.

Ejemplo 20.1 (Perturbación aditiva)

Para la configuración de la Figura 20.1, se ve fácilmente que

\[M=-K\left(I+P_{0} K\right)^{-1} W=-\left(I+K P_{0}\right)^{-1} K W\nonumber\]

Ejemplo 20.2 (Perturbación Multiplicativa)

Una perturbación multiplicativa de la forma de la Figura 20.2 se puede insertar en el sistema de bucle cerrado ya sea en la entrada o salida de la planta. El procedimiento es entonces idéntico al Ejemplo 20.1, excepto que\(M\) se convierte en una función diferente. Nuevamente se verifica fácilmente que para una perturbación multiplicativa en la entrada de la planta,

\[M=-\left(I+K P_{0}\right)^{-1} K P_{0} W \ \tag{20.11}\]

mientras que una perturbación en los rendimientos de salida

\[M=-\left(I+P_{0} K\right)^{-1} P_{0} K W \ \tag{20.12}\]

Lo que muestran los ejemplos anteriores es que la robustez de estabilidad requiere asegurar que las versiones ponderadas de ciertas funciones de transferencia familiares tengan\(\mathcal{H}_{\infty}\) normas que sean menores a 1. Por ejemplo, con una perturbación multiplicativa en la salida como en el último ejemplo, lo que requerimos para la robustez de estabilidad es\(\|T W\|_{\infty}<1\), donde\(T\) está la función de sensibilidad complementaria asociada al sistema nominal de bucle cerrado. Esta condición evidentemente tiene el mismo sabor que las condiciones que discutimos anteriormente en relación con el rendimiento nominal del sistema de bucle cerrado.

El teorema de la pequeña ganancia no logra aprovechar ninguna estructura especial que pueda haber en el conjunto de incertidumbre\(\Delta\), y por lo tanto puede ser muy conservador. Como ejemplos de los tipos de situaciones que se presentan, considere los siguientes dos ejemplos.

Ejemplo 20.3

Supongamos que tenemos un sistema que está mejor representado por el modelo de la Figura 20.4. Cuando este sistema se reduce a la forma estándar,\(\Delta\) tendrá un bloque diagonal

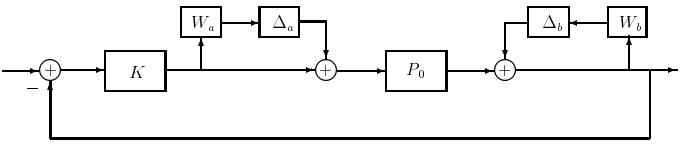
Figura 20.4: Planta con múltiples incertidumbres.

estructura, ya que las dos perturbaciones entran en diferentes puntos del sistema:

\ [\ Delta=\ left [\ begin {array} {cc}
\ Delta_ {a} & 0\\
0 &\ Delta_ {b}
\ end {array}\ derecha]\\ tag {20.13}\]

Así, hay alguna información agregada sobre la incertidumbre de la planta que no puede- ser capturada por el teorema de pequeña ganancia no estructurada, y en general, aunque\(\|M\|_{\infty} \geq 1\) por lo\(M\) que corresponda a\(\Delta\) lo anterior, puede que no haya perturbación admisible que resulte en inestabilidad\((I-M \Delta)^{-1}\).

Ejemplo 20.4

Supongamos que además de los límites de norma sobre la incertidumbre, sabemos que la fase de la perturbación permanece en el sector\(\left[-30^{\circ}, 30^{\circ}\right]\). Nuevamente, aunque\(\|M\|_{\infty} \geq 1\) por\(M\) lo que corresponda al\(\Delta\) para este sistema, no puede haber perturbación admisible que resulte en inestabilidad\((I-M \Delta)^{-1}\).

En ambos de los dos ejemplos anteriores, el teorema de pequeña ganancia no estructurada da resultados conservativos.

Relación de la Robustez de Estabilidad con el Criterio Nyquist (SISO)

Supongamos que tenemos una planta nominal SISO con una perturbación multiplicativa y un controlador nominalmente estabilizador\(K\). Entonces\(P=P_{0}(1+W \Delta)\), y la función de transferencia de bucle abierto compensada es

\[P K=P_{0} K+P_{0} K W \Delta \ \tag{20.14}\]

Dado que\(P_{0}\)\(K\),, y\(W\) son conocidos y\(|\Delta| \leq 1\) con fase arbitraria, podemos deducir de (20.14) que la gráfica Nyquist “real” a cualquier frecuencia dada\(\omega_{0}\) está contenida en una región delimitada por un círculo centrado en\(P_{0}\left(j \omega_{0}\right) K\left(j \omega_{0}\right)\), con radio\(\left|P_{0} K W\left(j \omega_{0}\right)\right|\). Esto se ilustra en la Figura 20.5 (a). Claramente, si el círculo de incertidumbre alguna vez incluye\(-1\), existe la posibilidad de que la trama nyquista “real” tenga un cerco extra, y por lo tanto sea inestable. Podemos relacionarlo con el problema de estabilidad robusta de la siguiente manera. Del Ejemplo 20.2, el sistema SISO es robustamente estable por el teorema de pequeña ganancia si

\[\left|\frac{P_{0} K}{1+P_{0} K} W\right|<1, \quad \forall \omega \ \tag{20.15}\]

Equivalentemente,

\[\left|P_{0} K W\right|<\left|1+P_{0} K\right| \ \tag{20.16}\]

El lado derecho de (20.16) es la magnitud de una traslación de la gráfica Nyquist de la función de transferencia de bucle nominal. En la Figura 20.5 (b), debido a la traducción, el cerco de cero desestabilizará el sistema. Claramente, esto no puede suceder si (20.16) está satisfecho. Esto deja clara la relación de estabilidad robusta con el criterio de SISO Nyquist.

Rendimiento como estabilidad Robustez

Supongamos que, para algún modelo de planta\(P\), deseamos diseñar un controlador de retroalimentación que no solo estabilice la planta (¡primer orden de prioridad!) , sino que también proporciona algunos beneficios de rendimiento, como una mejor regulación de la salida en presencia de perturbaciones. Dado que algo se sabe

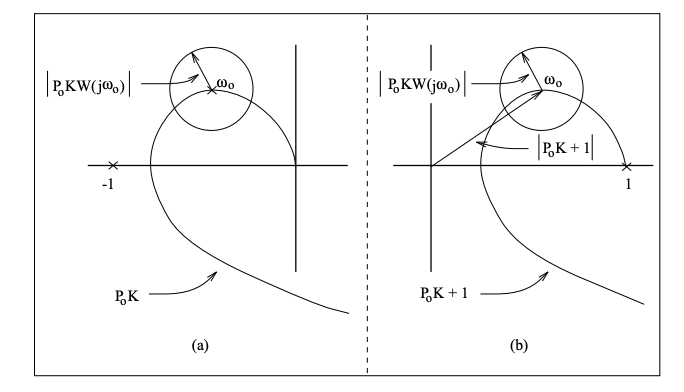
Figura 20.5: Relación del criterio de Nyquist y estabilidad robusta.

sobre el espectro de frecuencias de tales perturbaciones, el modelo del sistema podría parecerse a la Figura 20.6, donde\(\|\xi\|_{2}<1\), y el filtro de modelado se\(W\) puede construir para capturar las características de frecuencia de la perturbación. Calculando la función de transferencia de este bucle de\(\xi\) a\(y\), tenemos eso\(y=(I+P K)^{-1} W \xi\). Suponemos que la especificación de rendimiento se cumplirá si\(\left\|(I+P K)^{-1} W\right\|_{\infty}<1\), lo que no restringe el problema, ya que siempre se\(W\) puede escalar para reflejar la magnitud real de la perturbación o especificación de rendimiento. Esta formulación parece análoga a un problema de estabilidad robusta, y de hecho, se puede verificar que el teorema de pequeña ganancia aplicado al sistema de la Figura 20.7 captura la restricción idéntica en la función de transferencia del sistema. Al mapear este sistema en la forma estándar de la Figura 20.3, encontramos que\(M=(I+P K)^{-1} W\), que es exactamente lo\(M\) que se necesita si la condición de pequeña ganancia es producir la condición deseada

Por último, la incertidumbre de la planta tiene que ser puesta en escena simultáneamente con el

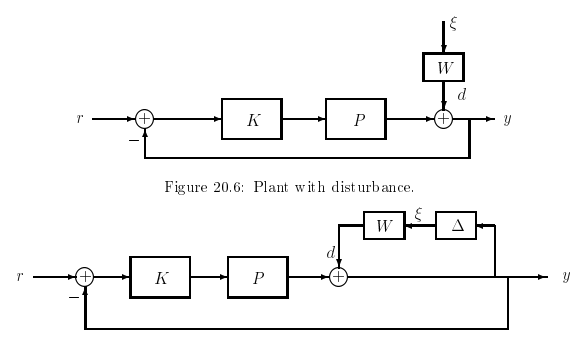
Figura 20.7: Mapeo de especificaciones de desempeño en un problema de estabilidad.

restricciones de rendimiento. Esto es necesario para formular el problema de robustez del desempeño. Debe ser evidente que esto conducirá a situaciones con bloque diagonal\(\Delta\), como se obtuvo en el contexto del último ejemplo en la subsección anterior. El tratamiento de este caso requerirá la noción de valores singulares estructurados, como veremos en la siguiente conferencia.