21.7: Rango uno

Aunque no contamos con métodos para computar\(\mu\) exactamente, hay una situación particular en la que esto es posible. Esta situación ocurre si\(M\) tiene rango 1, es decir

\[M=a b^{*}\nonumber\]

donde\(a, b \in \mathbb{C}^{n}\). Entonces se deduce que\(\mu\) con respecto a\(\Delta_{0}\) contener perturbaciones diagonales complejas viene dada por

\[\frac{1}{\mu(M)}=\inf _{\Delta \in \Delta_{0}}\left\{\sigma_{\max }(\Delta) \mid \operatorname{det}(I-M \Delta)=0\right\}\nonumber\]

Sin embargo,

\ [\ begin {alineado}
\ nombreoperador {det} (I-M\ Delta) &=\ nombreoperador {det}\ izquierda (I-a b^ {*}\ Delta\ derecha)\\
&=\ nombreoperador {det}\ izquierda (I-b^ {*}\ Delta a\ derecha)
\ end {alineado}\ nonumber\]

\ [\ begin {array} {l}
=\ operatorname {det}\ left (I-\ left [\ Delta_ {1}\ cdots\ Delta_ {n}\ derecha]\ left [\ begin {array} {c}
\ overline {b_ {1}} a_ {1}\
\ overline {b_ {2}} a_ {2}\
\ vdots\\
b_ {n} a_ {n}
\ end {array}\ derecha]\ derecha)\\
= 1-\ izquierda [\ Delta_ {1}\ cdots\ Delta_ {n}\ derecha]\ izquierda [\ begin {array} {c}
b_ {1} a_ {1}\\
b_ {2} a_ {2} a_ {2}
\\ vdots\\
b_ {n} a_ {n}
\ end {array}\ derecha]
\ end {array}\ nonumber\]

y\(\sigma_{\max }(\Delta)=\max _{i}\left|\Delta_{i}\right|\). Por lo tanto,

\ [\ frac {1} {\ mu (M)} =\ inf _ {\ Delta_ {1},\ ldots,\ Delta_ {n}}\ izquierda\ {\ max _ {i}\ izquierda|\ Delta_ {i}\ derecha|\ izquierda [\ izquierda [\ Delta_ {1}\ cdots\ Delta_ {n}\ derecha]\ izquierda [\ begin {array} {c}
\ overline {b_ {1}} a_ {1}\\
b_ {2} a_ {2}\\
\ vdots\\
b_ {n} a_ {n}
\ end {array }\ derecha] =1\ derecha\}\ derecha. \ nonumber\]

Optimizando el RHS, se deduce que (verificar)

\[\frac{1}{\mu(M)}=\frac{1}{\sum_{i=1}^{n}\left|\overline{b_{i}} a_{i}\right|} \leftrightarrow \mu(M)=\sum_{i=1}^{n}\left|\overline{b_{i}} a_{i}\right|\nonumber\]

Observe que el problema de rechazo de perturbaciones robustas de SISO es un problema de rango uno. Esto sigue desde

\ [M=\ left [\ begin {array} {c}
-W_ {1} K\\
W_ {2}
\ end {array}\ right]\ left [\ frac {P_ {0}} {1+P_ {0} K}\ quad\ frac {1} {1+P_ {0} K}\ derecha]\ nonumber\]

Entonces

\[\mu(M(j \omega))=\left|\frac{W_{1} P_{0} K}{1+P_{0} K}(j \omega)\right|+\left|\frac{W_{2}}{1+P_{0} K}(j \omega)\right|\nonumber\]

que es la condición que derivamos antes.

Perturbaciones del factor coprimo

Considere la clase de sistemas SISO

\[\Omega=\left\{\frac{N(s)}{D(s)} \mid N=N_{0}+\Delta_{1} W_{1}, D=D_{0}+\Delta_{2} W_{2},\left\|\Delta_{i}\right\|<1\right\}\nonumber\]

donde la planta nominal es\(N_{0}/D_{0}\) con la propiedad que ambos\(N_{0}\) y\(D_{0}\) son estables sin ceros comunes en el RHP. Supongamos que\(K\) se estabiliza\(N_{0}/D_{0}\). Este diagrama de bloques se muestra en la Figura 21.7.

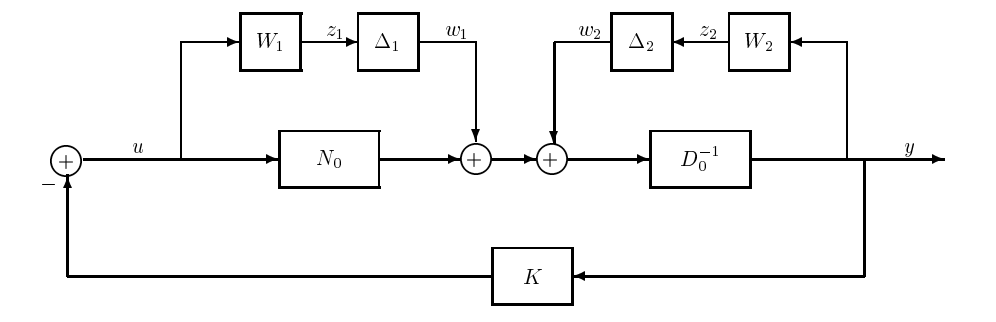
Figura 21.7: Modelo de perturbación del factor coprimo

El diagrama de bloques de bucle cerrado se puede asignar al\(M- \Delta\) diagrama donde

\ [\ begin {alineado}
M &=\ left [\ begin {array} {cc}
-\ frac {W_ {1} K} {D_ {0} +N_ {0} K} & -\ frac {W_ {1} K} {D_ {0} +N_ {0} K}\\
\ frac {W_ {2}} {D_ {0} +N_ {0} +N_ {0} _ {0} K} &\ frac {W_ {2}} {D_ {0} +N_ {0} K}
\ end {array}\ right]\\
&=\ left [\ begin {array} {c}
-\ frac {W_ {1} K} {D_ {0} +N_ {0} K}\\
\ frac {W_ {2}} {D_ {0} +N_ {0} K}
\ final {matriz}\ derecha] [1\ 1]
\ final {alineado}\ nonumber\]

De ahí,\(M\) tiene rango 1 y

\[\mu(M(j \omega))=\left|\frac{W_{1} K}{D_{0}+N_{0} K}\right|+\left|\frac{W_{2}}{D_{0}+N_{0} K}\right|\nonumber\]

Estabilidad robusta de Hurwitz de polinomios con perturbaciones complejas

Otra aplicación del valor singular estructurado con matrices de rango uno es la estabilidad robusta de una familia de polinomios con perturbaciones complejas de los coefcientes. En este caso vamos a\ (\ delta =\ left [\ begin {array} {cccc}
\ delta_ {n-1} &\ delta_ {n-2} &\ ldots &\ delta_ {0}
\ end {array}\ right] ^ {T}\) y considerar la familia polinómica

\[P(s, \delta)=s^{n}+\left(a_{n-1}+\gamma_{n-1} \delta_{n-1}\right) s^{n-1}+\ldots+\left(a_{0}+\gamma_{0} \delta_{0}\right)\nonumber\]

dónde\(a_{i}\),\(\gamma_{i}\), y\(\delta_{i} \in \mathbb{C}\) y\(\left|\delta_{i}\right| \leq 1\). Queremos obtener una condición que sea necesaria y suficiente para la estabilidad de Hurwitz de toda la familia de polinomios\(P(s, \delta)\). Podemos escribir los polinomios de esta familia como

\[P(s, \delta)=P(s, 0)+\tilde{P}(s, \delta)\label{21.20}\]

\ [=\ izquierda (s^ {n} +a_ {n-1} s^ {n-1} +\ ldots+a_ {0}\ derecha) +\ izquierda (\ gamma_ {n-1}\ delta_ {n-1} s^ {n-1} +\ ldots+\ gamma_ {0}\ delta_ {0}\ derecha)\ etiqueta {21.21}\)

que también se puede reescribir como

\ [P (s,\ delta) =P (s, 0) +\ left [\ begin {array} {ccc}
1 &\ ldots 1\ end {array}
\ right]\ left [\ begin {array} {ccccc}
\ delta_ {n-1} & 0 &\ ldots & 0\\ ldots & 0\\
0 &\ delta_ {n-2} & 0 &\ ldots & 0\\
\ vdots & & amp;\ ddots & &\ vdots\\
& & &\ delta_ {1} & 0\\\
0 & 0 &\ ldots & 0 &\ delta_ {0}
\ end {array}\ right]\ left [\ begin {array} {c}
\ gamma_ {n-1} s^ {n-1}
\\ gamma_ {n-2} s^ {n-2}\
\ vdots\\
\ gamma_ {1} s\\
\ gamma_ {0}
\ end {array}\ derecha]\ nonumber\]

Suponemos que el polinomio central\(P(s, 0)\) es el establo de Hurwitz. Esto implica que la estabilidad de toda la familia\(P(s, \delta)\) es equivalente a la condición de que

\ [1+\ frac {1} {P (j\ omega, 0)}\ left [\ begin {array} {ccc}
1 &\ ldots 1\ end {array}
\ right]\ left [\ begin {array} {ccccc}
\ delta_ {n-1} & 0 &\ ldots & 0\\ ldots & 0\\ 0 &\
0 &\ delta_ {n-2} & 0 &\ ldots & 0\\
\ vdots & amp; &\ ddots & &\ vdots\\
& & &\ delta_ {1} & 0\\\ 0 &\ ldots &
0 &\ delta_ {0}\ end {array}
\ derecha]\ izquierda [\ begin {array} {c}\ gamma_ {n-1} (j
\ omega) ^ {n-1}\\ gamma_ {n-2} (j\ omega) ^ {n-1}
\\ gamma_ {n-2} (j\ omega) ^ {n-2}\\
\ vdots\\
\ gamma_ {1} (j\ omega)\
\ gamma_ {0}
\ end {array}\ derecha]\ neq 0\ nonumber\]

para todos\(\omega \in \mathbb{R}\) y\(\left|\delta_{i}\right| \leq 1\). Esto equivale a la condición de que

\ [\ nombreoperador {det}\ left (I+\ frac {1} {P (j\ omega, 0)}\ left [\ begin {array} {c}
\ gamma_ {n-1} (j\ omega) ^ {n-1}
\\ gamma_ {n-2} (j\ omega) ^ {n-2}\
\ vdots\
\ gamma_ {1} (j\ omega)\\
\ gamma_ {0}
\ end {array}\ derecha]\ izquierda [\ begin {array} { lll}
1 & 1 &\ ldots 1
\ end {array}\ right]\ Delta\ right)\ neq 0\ nonumber\]

para todos\(\omega \in \mathbb{R}\) y\(\Delta \in \Delta\) con\(\|\Delta\|_{\infty} \leq 1\). Ahora usando el concepto del valor singular estructurado llegamos a la siguiente condición que es necesaria y suficiente para la estabilidad de Hurwitz de toda la familia

\[\mu(M(j \omega))<1\nonumber\]

para todos\(\omega \in \mathbb{R}\), donde

\ [M (j\ omega) =\ frac {1} {P (j\ omega, 0)}\ left [\ begin {array} {c}
\ gamma_ {n-1} (j\ omega) ^ {n-1}\
\ gamma_ {n-2} (j\ omega) ^ {n-2}\
\ vdots\
\ gamma_ {1} (j\ omega)\\
\ gamma_ {0}
\ end {array}\ derecha]\ izquierda [\ begin {array} {lll}
1 & 1 &\ ldots 1
\ end {array}\ derecha]\ nonumber\]

Claramente esta es una matriz de rango uno y por nuestra discusión previa el valor singular estructurado puede calcularse analíticamente dando como resultado la siguiente prueba

\[\frac{1}{|P(j \omega, 0)|} \sum_{i=1}^{n}\left|\gamma_{n-i}\right||\omega|^{n-i}<1\nonumber\]

para todos\(\omega \in \mathbb{R}\).