22.4: Ejercicios

Ejercicio\(\PageIndex{1}\)

Supongamos que se le da la entrada única, sistema de orden n\(x(k + 1) = Ax(k) + bu(k)\), y asuma que el control\(u\) cada vez que el paso se limita a estar en el intervalo [0, 1]. Supongamos también que un valor propio de\(A\), digamos\(\lambda_{1}\), es real y no negativo. Mostrar que el conjunto de estados alcanzables desde el origen está confinado a un lado de un hiperplano a través del origen en\(\mathcal{R}^{n}\). (Pista: Un vector propio asociado con te\(\lambda_{1}\) ayudará a hacer el argumento.)

[Un hiperplano a través del origen es un subespacio (n - 1) -dimensional definido como el conjunto de vectores\(x\) en\(\mathcal{R}^{n}\) para los cuales\(a^{\prime} x=0\), donde\(a\) hay algún vector fijo distinto de cero en\(\mathcal{R}^{n}\). Evidentemente\(a\) es normal al hiperplano. Los dos “lados” del hiperplano, o los dos “medios espacios” definidos por él, son los conjuntos de\(x\) para los cuales\(a^{\prime} x \leq 0\) y\(a^{\prime} x \geq 0\).]

Ejercicio\(\PageIndex{2}\)

Dado el sistema

\ [x (k+1) =\ left (\ begin {array} {cc}
a & b\\
0 & c
\ end {array}\ right) x (k) +\ left (\ begin {array} {c}
d\\
e
\ end {array}\ derecha) u\ tag {k}\]

donde\(a, b, c, d, e\) están los escalares, deducir con precisión qué condición satisfacen estos coeficientes cuando el sistema no es alcanzable. Dibuja un diagrama de bloques correspondiente al sistema anterior y utilízalo para interpretar los siguientes casos especiales en los que se pierde la alcanzabilidad: (a) e = 0; (b) b = 0 y d = 0; (c) b = 0 y c = a.

Ejercicio\(\PageIndex{3}\)

(a) Dado el sistema de entrada m\(x(k+1)=A x(k)+B u(k)\), donde\(A\) está la matriz jordano-forma

\ [A=\ left (\ begin {array} {lllll}
2 & 1 & 0 & 0 & 0 &
0\\ 0 & 2 & 0 & 0 &
0 & 0 & 0 & 2 & 0 &
0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 3
\ end {array} \ derecha)\ nonumber\]

obtener condiciones que sean necesarias y suficientes para que el sistema sea accesible. (Pista: Tus condiciones deben involucrar las filas\(b_{i}\) de\(B\). Alguna forma de la prueba de alcanzabilidad modal lo hará, ¡no es sorprendente! - llevar a la solución más simple.)

(b) Generalizar este resultado de alcanzabilidad al caso en que\(A\) se encuentre una matriz general\(n \times n\) de forma jordano.

(c) Dado el sistema de entrada única y accesible\(x(k + 1) = Ax(k) + bu(k)\), muestran que solo puede haber un bloque Jordan asociado a cada valor propio distinto de\(A\).

Ejercicio\(\PageIndex{4}\)

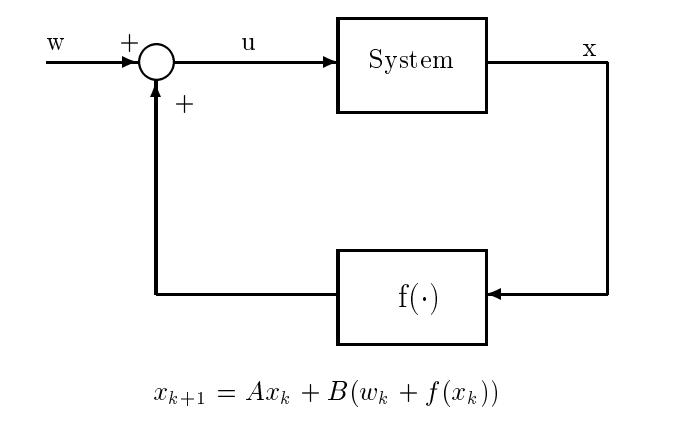
Dado el sistema alcanzable n-dimensional\(x(k + 1) = Ax(k) + Bu(k)\), supongamos que\(u(k)\) se genera de acuerdo con el esquema de retroalimentación no lineal mostrado en la figura, donde\(u(k) = w(k) + f (x(k))\), al\(f (.)\) ser una función arbitraria pero conocida, y\(w(k)\) siendo la nueva entrada de control para el bucle cerrado sistema.

Mostrar que siempre se\(w(k)\) puede elegir para llevar el estado del sistema desde el origen a cualquier estado objetivo especificado en no más de n pasos. De este modo, habrás demostrado que la alcanzabilidad se conserva bajo retroalimentación de estado (incluso no lineal).

Ejercicio\(\PageIndex{5}\)

Considere el siguiente Sistema SISO lineal,\(\Sigma\):

\ [\ comenzar {alineado}
x (k+1) &=A (k) x (k) +B (k) u (k)\\
y (k) &=C (k) x (k) +D (k) u (k)
\ final {alineado}\ nonumber\]

donde\(A(k)=A(k+N) \forall k \geq 0\), de manera similar para B (k), C (k) y D (k)

(a) Mostrar que\(\Sigma\) es N-Periódico, es decir, para cero condiciones iniciales, mostrar que si y es la respuesta de salida para alguna entrada u, entonces\(y(k - N)\) es la respuesta de salida para\(u(k - N)\). Asumir por simplicidad que\(u(k) = 0\) para\(k < 0\). Queremos obtener una representación diferente de este sistema con la que sea más fácil trabajar. Para lograrlo, agruparemos todas las entradas\(N\) sucesivas a partir de\(k = 0\). También haremos lo mismo para la salida. Para ser más precisos, definiremos un mapeo\(L\), llamado levantamiento, tal que

\[L:(u(0), u(1), u(2), \ldots, u(k), \ldots) \rightarrow \tilde{u}\nonumber\]

donde

\ [\ tilde {u} =\ left (\ left (\ begin {array} {c}
u (0)\\
u (1)\\
\ vdots\\
u (N-1)
\ end {array}\ right),\ left (\ begin {array} {c}
u (N)\\
u (N+1)\\
\ vdots\\
u (2 N-1)
\ end {array }\ derecha),\ cdots,\ left (\ begin {array} {c}
u (k N)\\
u (k N+1)\\
\ vdots\\
u ((k+1) N-1)
\ end {array}\ derecha),\ cdots\ derecha)\ nonumber\]

Del mismo modo,\(L: y \rightarrow \tilde{y}\)

(b) Demostrar que el mapeo del sistema\(\tilde{u}\) a\(\tilde{y}\) es lineal invariable en el tiempo. Esto lo denotaremos por\(\tilde{\Sigma}\), el sistema levantado. Cuáles son las dimensiones de las entradas y salidas. (Es decir, al levantar las entradas y salidas, nos deshicimos de la periodicidad del sistema y obtuvimos un Sistema Multi-Input Multi-Output).

c) Dar una descripción estado-espacial del sistema levantado. (Pista: Elija como variable de estado\(\tilde{x}(k)=x(k N)\), es decir, muestras del vector de estado original. Justifica esta elección.

d) Demostrar que el subespacio alcanzable del sistema levantado\(\tilde{\Sigma}\) está incluido en el subespacio alcanzable del sistema periódico\(\Sigma\). Mostrar que lo contrario es cierto si el sistema periódico es accesible en\(T\) pasos con\(T = rN\) (un múltiplo del periodo).

e) ¿Es cierto que la alcanzabilidad del sistema periódico\(\Sigma\) implica la alcanzabilidad del sistema levantado\(\tilde{\Sigma}\)? Demostrar o mostrar un contraejemplo.