3.2: Caudal másico
- Page ID
- 86418
Antes de continuar, necesitamos desarrollar una mejor comprensión de cómo calcular el caudal másico. Recordemos que anteriormente definimos el caudal másico como el caudal de tiempo en el que la masa cruza el límite de un sistema. Tenga en cuenta que un caudal másico realmente solo tiene significado ya que se relaciona con el límite para el que se define.
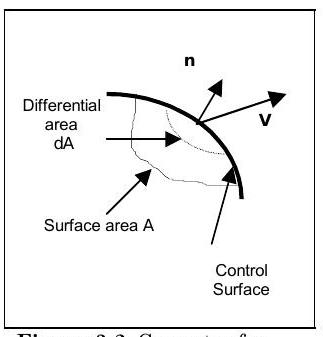
Figura\(\PageIndex{1}\): Geometría para el flujo a través de un límite del sistema.
Para calcular el caudal másico, considere la velocidad a la que la masa fluye a través del límite del sistema con el área\(A\) en la Figura\(\PageIndex{1}\). Por definición, el caudal másico de un sistema se define por la ecuación
\[ \dot{m}_{out} = \int\limits_{A_{sys}} \rho \left( \mathbf{V}_{rel} \cdot \mathbf{n} \right) \, dA \nonumber \]
donde
\[ \begin{align*} \rho &= \text{the fluid density,} \\ \mathbf{V}_{rel} &= \text{velocity (a vector) of the mass crossing the boundary measured with respect to the system boundary, and} \\ \mathbf{n} &= \text{is the unit vector normal to the differential area } dA \text{ and pointing out of the system.} \end{align*} \nonumber \]
La clave para entender el significado de la Ec. \(\PageIndex{1}\)es recordar el significado de un simple escalar o punto producto de dos vectores. Primero recordemos que el producto escalar o punto de dos vectores produce un escalar. Ahora aplicando la definición de una esta operación al vector normal de la unidad y el vector de velocidad da:
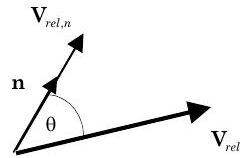
Figura\(\PageIndex{2}\): Definición del producto punteado de\(\vec{V}_{rel}\) y\(\hat{n}\).
\[ \begin{align*} V_{rel, n} &= |\mathbf{V}_{rel, n}| \\ &= \mathbf{V} \cdot \mathbf{n} = |\mathbf{V}| |\mathbf{n}| \cos \theta \\ &= \text{normal velocity of the mass relative to the boundary surface} \end{align*} \nonumber \]
Usando este resultado, la expresión del caudal másico se puede escribir como
\[ \dot{m} = \int\limits_{A_{sys}} \rho V_{rel, n} \, dA \nonumber \]
En general, la densidad\(\rho\) y la velocidad normal\(V_{rel,n}\) pueden cambiar con la posición en la superficie límite. También tenga en cuenta que hemos bajado el subíndice “out” porque nuestra observación de la dirección de\(V_{rel,n}\) con respecto al sistema determina si el caudal másico está dentro o fuera del sistema.
Existen numerosos supuestos de modelado que se utilizan para describir el comportamiento de los sistemas reales en la construcción de modelos matemáticos. Si el flujo tiene una densidad uniforme en el límite del flujo, entonces la densidad es espacialmente uniforme en el límite del flujo. En estas condiciones,
\[ \dot{m} = \int\limits_{A_c} \rho V_{rel, n} \, dA = \rho \underbrace{ \int\limits_{A_c} V_{rel, n} \, dA } _{= \dot{ V\kern-0.8em\raise0.3ex- }} = \rho \dot{ V\kern-0.8em\raise0.3ex- }, \nonumber \]
más simplemente expresado como
\[ \dot{m} = \rho \dot{ V\kern-0.8em\raise0.3ex- } \quad \text{(uniform density)} \nonumber \]
donde la integral de la velocidad normal relativa sobre el área de la sección transversal del flujo es el caudal volumétrico,\(\dot{ V\kern-0.8em\raise0.3ex- }\). Las dimensiones del caudal volumétrico son\([\text{L}]^3/[\text{T}]\) y las unidades típicas están\(\text{m}^3/\text{s}\) en SI y\(\text{ft}^3/\text{s}\) en AES. Hay muchas otras unidades de uso común para el caudal volumétrico, incluyendo galones por min (\(\text{gpm}\)) y pies cúbicos por min (\(\text{cfm}\)).
Si nos limitamos a límites de flujo planos (planos), entonces son posibles varias simplificaciones adicionales. Si el flujo en un límite tiene una velocidad uniforme y una densidad uniforme, tanto la densidad como la velocidad relativa salen de la integral y el caudal másico se convierte en
\[ \dot{m} = \rho A_c V_n \nonumber \]
Esta es una de las formas más utilizadas para calcular el caudal másico. Observe que hemos bajado el subíndice “rel” para simplificar la notación; sin embargo, se le advierte que todos los caudales másticos y volumétricos deben calcularse necesariamente con respecto a un límite de flujo. Para condiciones de flujo donde la densidad y la velocidad normal varían a través de la sección transversal del flujo, es una práctica común romper la sección transversal del flujo en muchos elementos pequeños donde la Ec. \(\PageIndex{4}\)aplica y luego suma los resultados, e.g\(\dot{m} = \sum_{j} \left( \rho A_c V_{rel, n} \right) _j \). En muchos casos, la velocidad variará a través de la sección transversal pero la densidad será relativamente uniforme. Bajo estas condiciones es frecuentemente útil escribir el caudal másico en términos de una velocidad promedio\(V_{n, avg}\).
\[ \dot{m} = \rho A_c V_{n, avg} \quad \text{where } V_{n, avg} = \frac{ \dot{m} }{\rho A_c} = \frac{ \dot{ V\kern-0.8em\raise0.3ex- } }{A_c} \nonumber \]
El aire fluye de manera constante a través de un conducto de calentamiento con una sección transversal cuadrada\(2H \times 2H\). El perfil de velocidad medido sobre el área de la sección transversal se puede describir matemáticamente en términos de la posición en el conducto\((x, \, y)\) y la velocidad de la línea central\(V_o\) (velocidad a (0,0)).
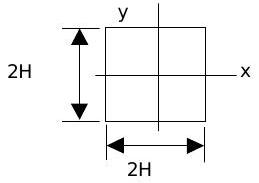
\[ V_n = V_o \left[ 1 - \left( \frac{x}{H} \right)^2 \right] \left[ 1 - \left( \frac{y}{H} \right)^2 \right] \nonumber \]
Determinar:
(a) el caudal volumétrico, en\(\text{m}^3/\text{s}\), si\(V_o = 10 \text{m/s}\) y\(H = 0.3 \text{m}\), y
(b) la relación de\(V_{avg}\) a\(V_o\).
Solución
Conocido: El aire fluye en un conducto cuadrado con un perfil de velocidad especificado.
Encuentre: (a) Caudal volumétrico si\(V_o = 10 \text{m/s}\) y\(H = 0.3 \text{m}\). (b) Proporción de\(V_{avg}\) a\(V_o\).
Dado: Croquis y perfil de velocidad mostrados arriba.
Análisis: Estrategia\(\rightarrow\) Dado que se dan Vn y el área, utilice la definición de caudal volumétrico. Comenzamos con la definición de caudal volumétrico
\[ \begin{align*} \dot{ V\kern-0.8em\raise0.3ex- } &= \int\limits_{A_c} V_n \, dA \quad \text{where } dA = dx \ dy \\ &= \int\limits_{-H}^{H} \int\limits_{-H}^{H} \underbrace{ V_o \left[ 1 - \left( \frac{x}{H} \right)^2 \right] \left[ 1 - \left( \frac{y}{H} \right)^2 \right] }_{V_n} \, \underbrace{ dx \ dy }_{dA} \end{align*} \nonumber \]
Llevando\(V_o\) fuera de lo integral y usando la simetría para cambiar los límites de la integración, tenemos
\[ \dot{V} = 4 V_o \int\limits_{0}^{H} \int\limits_{0}^{H} \underbrace{ \left[ 1 - \left( \frac{x}{H} \right)^2 \right] \left[ 1 - \left( \frac{y}{H} \right)^2 \right] }_{V_n} \underbrace{ dx \ dy }_{dA} \nonumber \]
Integrando primero con respecto al\(x\) eje -da
\[ \int\limits_{0}^{H} \left[ 1 - \left( \frac{x}{H} \right)^2 \right] \ dx = \left[ x - \frac{1}{3} \frac{x^3}{H^2} \right]_0^H = \frac{2}{3} H \nonumber \]
Sustituyendo de nuevo a la integral completa e integrándose con respecto a\(y\) da
\[ \begin{align*} \dot{ V\kern-0.8em\raise0.3ex- } &= 4 V_o \left( \frac{2}{3} H \right) \int\limits_{0}^{H} \left[ 1 - \left( \frac{y}{H} \right)^2 \right] \ dy = 4 V_o \left( \frac{2}{3} H \right) \left[ y - \frac{1}{3} \frac{y^3}{H^2} \right]_0^H = 4 V_o \left[ \frac{2}{3} H \right]^2 \\ &= \frac{16}{9} H^2 V_o \end{align*} \nonumber \]
Sustituir los números en esta expresión da el caudal volumétrico como
\[ \dot{ V\kern-0.8em\raise0.3ex- } = \frac{16}{9} \left( 0.3 \ \text{m} \right)^2 \left( 10 \ \frac{ \text{m} }{ \text{s} } \right) = 1.6 \ \text{m}^3 / \text{s} \nonumber \]
Ahora, para encontrar la relación entre la velocidad promedio y la velocidad de la línea central, use la definición de la velocidad promedio:
\[ V_{avg} = \frac{ \dot{m} }{\rho A_c} = \frac{\dot{ V\kern-0.8em\raise0.3ex- }}{A_c} = \frac{ \frac{16}{9} H^2 V_o }{ \left[ 2H \right]^2 } = \frac{4}{9} V_o \nonumber \]
Así, la velocidad promedio es\(\dfrac{4}{9}\) de la velocidad de la línea central.
El agua fluye constantemente en un río. La sección transversal del río se muestra en la siguiente figura. Además, también se muestran las velocidades superficiales medidas observando las piezas de madera flotando aguas abajo.
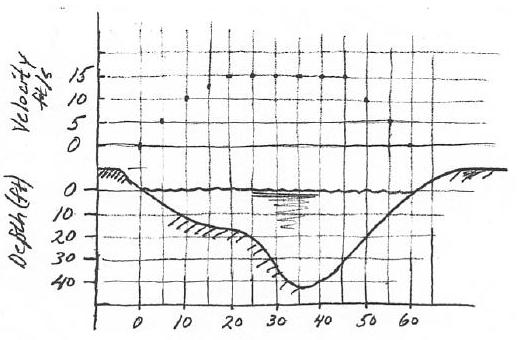
Calcular el (a) caudal volumétrico en\(\text{ft}^3/ \text{s}\) y (b) caudal másico si la densidad del agua es\(62.4 \ \text{lbm/ft}^3\).
Solución
Conocido: Velocidades en la superficie de un río y la profundidad del río en cada ubicación.
Encuentra: Caudal volumétrico adentro\(\text{ft}^3/\text{s}\) y el caudal másico si\(\rho = 62.4 \text{lbm/ft}^3\).
Dado: Profundidad de canal y velocidad superficial dadas en la figura anterior.
Análisis:
Estrategia\(\rightarrow\) Debe ser capaz de aplicar la ecuación definitoria para el caudal volumétrico y másico.
Supongamos que la\(\rightarrow \) velocidad es uniforme de arriba a abajo del canal. La ecuación definitoria para el caudal volumétrico es
\[ \begin{align*} \dot{ V\kern-0.8em\raise0.3ex- } &= \int\limits_{A_{surface}} V_n \, dA \\ &\simeq \sum_{i=1}^{N} A_{i} V_{avg, \ i} \simeq \sum_{i=1}^{N}\left(h_{i} \Delta x_{i}\right) V_{avg, \ i} \end{align*} \nonumber \]
Para realizar la integración necesaria numéricamente, podemos configurar una tabla:
| \(i\) | \(x \,\, (\text{ft})\) | \(V_n \,\, (\text{ft/s})\) | \(\Delta x\,\, (\text{ft})\) | \(h_i\,\, (\text{ft})\) | \(V_n (h \Delta x)\,\,(\text{ft}^3/\text{s})\) |
|---|---|---|---|---|---|
| \ (i\) ">\(1\) | \ (x\,\, (\ text {ft})\) ">\(2.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(2.5\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(2.5\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(31.25\) |
| \ (i\) ">\(2\) | \ (x\,\, (\ text {ft})\) ">\(7.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(7.5\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(8.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(300.00\) |
| \ (i\) ">\(3\) | \ (x\,\, (\ text {ft})\) ">\(12.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(11.25\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(12.5\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(703.10\) |
| \ (i\) ">\(4\) | \ (x\,\, (\ text {ft})\) ">\(17.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(13.75\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(16.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(1100.00\) |
| \ (i\) ">\(5\) | \ (x\,\, (\ text {ft})\) ">\(22.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(15.0\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(18.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(1350.00\) |
| \ (i\) ">\(6\) | \ (x\,\, (\ text {ft})\) ">\(27.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(15.0\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(26.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(1950.00\) |
| \ (i\) ">\(7\) | \ (x\,\, (\ text {ft})\) ">\(32.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(15.0\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(37.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(2775.00\) |
| \ (i\) ">\(8\) | \ (x\,\, (\ text {ft})\) ">\(37.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(15.0\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(42.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(3150.00\) |
| \ (i\) ">\(9\) | \ (x\,\, (\ text {ft})\) ">\(42.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(15.0\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(36.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(2700.00\) |
| \ (i\) ">\(10\) | \ (x\,\, (\ text {ft})\) ">\(47.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(12.5\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(25.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(1562.50\) |
| \ (i\) ">\(11\) | \ (x\,\, (\ text {ft})\) ">\(52.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(7.5\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(15.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(562.50\) |
| \ (i\) ">\(12\) | \ (x\,\, (\ text {ft})\) ">\(57.5\) | \ (v_n\,\, (\ text {ft/s})\) ">\(2.5\) | \ (\ Delta x\,\, (\ text {ft})\) ">\(5\) | \ (h_i\,\, (\ text {ft})\) ">\(5.0\) | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(62.50\) |
| \ (i\) ">\(.\) | \ (x\,\, (\ text {ft})\) "> | \ (v_n\,\, (\ text {ft/s})\) "> | \ (\ Delta x\,\, (\ text {ft})\) "> | \ (h_i\,\, (\ text {ft})\) "> | \ (v_n (h\ Delta x)\,\, (\ text {ft} ^3/\ texto {s})\) ">\(16246.85\) |
Así, el caudal volumétrico promedio es\[ \dot{ V\kern-0.8em\raise0.3ex- } = 16.2 \times 10^3 \, \text{ft}^3/\text{s} \nonumber \]
El caudal másico se puede encontrar multiplicando la densidad del agua por el caudal volumétrico:
\[\dot{m} =\rho \dot{ V\kern-0.8em\raise0.3ex- } = \left(62.4 \ \frac{\mathrm{lb}_{\mathrm{m}}}{\mathrm{ft}^{3}}\right) \left(16200 \ \frac{\mathrm{ft}^{3}}{\mathrm{~s}} \right) = 1.01 \times 10^{6} \ \frac{\mathrm{lb}_{\mathrm{m}}}{\mathrm{s}} \nonumber \]
Comentario: Si reconocemos que la velocidad es máxima en la superficie libre y cero en la parte inferior, se podría obtener una mejor estimación asumiendo que la velocidad promedio es alguna fracción de la cantidad en la superficie libre. Por ejemplo, si asumimos que la velocidad promedio es\(4 / 5\) de la velocidad máxima, entonces el caudal volumétrico real es\(13.0 \times 10^{3} \, \mathrm{ft}^{3} / \mathrm{s}\).


