3.3: Conservación de la Ecuación de Masa
- Page ID
- 86442
El punto de partida recomendado para la aplicación de la ecuación de conservación de masa es la forma de tasa del balance de masas (ecuación de conservación de masa):
\[\frac{d m_{sys}}{d t} m= \sum_{in} \dot{m}_{i} - \sum_{out} \dot{m}_{e} \nonumber \]
donde\(m_{sys}=\int_{V_{ms}} \rho \ dV\), la masa del sistema, y\(\dot{m}\) es el caudal másico a través del límite del sistema.
Al aplicar la forma de tasa de la ecuación de conservación de masa a un sistema, hay muchos supuestos de modelado comunes que pueden usarse para configurar el modelo matemático del sistema físico. Estos se detallan en los siguientes párrafos.
Sistema de estado estacionario: Para un sistema de estado estacionario, todas las propiedades extensas y}\\) intensivas son independientes del tiempo. Así
\[\underbrace{\frac{d m_{sys}}{dt}}_{=0, \, \mathrm{SS}} = \sum_{in} \dot{m}_{i} - \sum_{out} \dot{m}_{e} \,\, \Rightarrow \,\, 0=\sum_{in} \dot{m}_{i}-\sum_{out} \dot{m}_{e} \nonumber \]
Sustancia incompresible: Una sustancia incompresible es aquella por la que la densidad nunca cambia. Bajo estas condiciones, el caudal másico puede escribirse en términos de densidad y caudal volumétrico:
\[ \begin{align*} &\dot{m} = \int\limits_{A_c} \rho V_{rel, n} \ dA = \rho \int\limits_{A_c} V_{rel, n} \ dA \,\, \Rightarrow \,\, \dot{m} = \rho \dot{V\kern-0.8em\raise0.3ex-} \\ &m_{sys} = \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} \rho \ d V\kern-0.5em\raise0.3ex- = \rho \int\limits_{V\kern-0.8em\raise0.3ex-_{sys}} \,\, \Rightarrow \,\, m_{sys} = \rho V\kern-0.8em\raise0.3ex-_{sys} \end{align*} \nonumber \]
Aunque no es una ley fundamental, la siguiente ecuación que involucra el volumen del sistema y los caudales volumétricos se utiliza a menudo para describir el comportamiento de los sistemas.
\[ \frac{d V\kern-0.8em\raise0.3ex- _{sys}}{dt} = \sum_{in} \dot{ V\kern-0.8em\raise0.3ex-}_i - \sum_{out} \dot{ V\kern-0.8em\raise0.3ex-}_{e} : \nonumber \]
¿Qué condiciones (o supuestos de modelado) deben aplicarse para que esta ecuación sea válida? Intente comenzar con la Ec. \(\PageIndex{1}\)y derivando esta ecuación para el volumen.
Flujo unidimensional con densidad uniforme en un límite de flujo: Bajo estas condiciones tanto la densidad como la velocidad salen fuera de la integral, dando
\[ \dot{m} = \int\limits_{A_c} \rho V_{rel, n} \ dA = \rho V_{rel, n} \int\limits_{A_c} dA \,\, \Rightarrow \,\, \dot{m} = \rho A_c V \nonumber \]
donde se supone que la velocidad\(V\) utilizada en el cálculo del caudal másico es el componente de la velocidad de la masa que cruza el límite que es normal al límite y medida en relación con el límite (independientemente de si el límite es móvil o estacionario).
Por favor, reconozca que no debe concentrarse ni memorizar la forma final de las ecuaciones desarrolladas anteriormente. Su enfoque debe estar en comprender los supuestos y aprender cómo impactan las ecuaciones gobernantes. Como encontrarás más adelante, los supuestos y su impacto serán utilizados repetidamente a lo largo de estas notas para ayudar a desarrollar modelos matemáticos para sistemas físicos.
También a veces se requiere aplicar la ecuación de conservación de masa a un proceso de tiempo finito cuando te interesa relacionar lo que se conoció en algún momento\(t_1\) con algún tiempo posterior\(t_2\). Nuevamente, en lugar de memorizar una forma especial de la ecuación, simplemente integre la forma de tasa de la ecuación de conservación de masa como se muestra a continuación:
\[\begin{align*} &\int\limits_{t_1}^{t_2} \left[ \frac{d m_{sys}}{dt} \right] \ dt = \int\limits_{t_1}^{t_2} \left[ \sum_{in} \dot{m}_i - \sum_{out} \dot{m}_e \right] \ dt \\[4pt] &\int\limits_{m_{sys, 1}}^{m_{sys, 2}} \ dm_{sys} = \int\limits_{t_1}^{t_2} \left( \sum_{in} \dot{m}_{i} \right) \ dt - \int\limits_{t_1}^{t_2} \left( \sum_{out} \dot{m}_{e} \right) \ dt \\[4pt] &m_{sys, 2} - m_{sys, 1} = \sum_{in} m_{i} - \sum_{out} m_{e} \end{align*} \nonumber \]donde
\(m_{sys, 2}; \, m_{sys, 1} \, =\)masa dentro del sistema en el tiempo\(t_2\) y\(t_1\), respectivamente.
\(m_{i} \equiv \int\limits_{t_1}^{t_2} \dot{m}_{i} \ dt \, =\)la cantidad de masa transportada al sistema durante el intervalo de tiempo\(t_1\) a\(t_2\). (¡Este NO es el cambio en la masa!)
Los siguientes ejemplos demuestran diversas aplicaciones de la ecuación de conservación de masa a diversos problemas.
Un matraz abierto se llena con acetona. Inicialmente, el matraz contiene\(25 \mathrm{~kg}\) acetona. Después de dos horas, parte de la acetona se evapora y el matraz contiene\(23 \mathrm{~kg}\) acetona. Tomando su sistema para que sea la acetona líquida, responda las siguientes preguntas aplicando conservación de masa:
¿Cuál es la acumulación de acetona durante las dos horas, en\(\mathrm{kg}\)?
¿Cuánta acetona se evaporó durante las dos horas, en\(\mathrm{kg}\)?
¿Cuál es la tasa promedio de evaporación durante este periodo de tiempo, en\(\mathrm{kg} / \mathrm{s}\)?
Solución
Conocido: La acetona se evapora de un matraz abierto
Encuentra: Acumulación de la acetona, en\(\mathrm{kg}\).
Cantidad de acetona que se evapora, en\(\mathrm{kg}\).
Tasa promedio de evaporación durante este periodo, en\(\mathrm{kg} / \mathrm{h}\).
Dado:
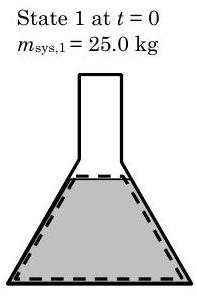
.jpg)
Análisis:
Estrategia\(\rightarrow\) ¿Cuál es el sistema? Acetona líquida como se sugiere en la declaración del problema.
¿Qué debemos contar? Masa de acetona.
¿Cuál es el periodo de tiempo? Periodo de tiempo finito de 2 horas.
Seleccionando la acetona líquida como sistema como se muestra en las figuras anteriores, tenemos un sistema abierto y solo hay una interacción con el entorno, el caudal másico de acetona fuera del sistema debido a la evaporación. Esto ocurre en la superficie libre del líquido en el matraz.
Escribiendo la forma de tasa de la ecuación de conservación de masa para este sistema tenemos
\[\frac{d m_{sys}}{dt} = \underbrace{ \cancel{ \sum_{in} \dot{m}_i } }_{\text {no inlet flows }}^{=0} \underbrace{ \cancel{ \sum_{out} \dot{m} i_e } }_{\text {only one outlet flow}} = \dot{m}_{\text {evap}} \quad \Rightarrow \quad \frac{d m_{\text {sys}}}{d t} = -\dot{m}_{\text {evap}} \nonumber \]
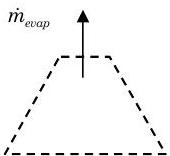
Figura\(\PageIndex{2}\): Velocidad de flujo másico fuera del sistema.
Para encontrar la acumulación, debemos entender que la acumulación de la masa en el sistema es el cambio en la masa del sistema
\[\Delta m_{sys} = m_{sys, 2} - m_{sys, 1} = (23.0 \mathrm{~kg})-(25.0 \mathrm{~kg})=-2.0 \mathrm{~kg} \nonumber \]Así, la acumulación de masa en el sistema es\(-2.0 \mathrm{~kg}\) de acetona.
Para encontrar la masa de acetona que se ha evaporado durante estas dos horas, debemos recurrir a la ecuación de conservación de masa desarrollada anteriormente. Como queremos que la cantidad de masa evaporada no la velocidad de evaporación, debemos integrar la ecuación de velocidad a lo largo del periodo de dos horas.
\[\frac{d m_{sys}}{d t} = -\dot{m}_{evap} \quad \rightarrow \quad \int\limits_{t_1}^{t_2} \left( \frac{d m_{sys}}{d t} \right) \ dt = \int\limits_{t_1}^{t_2} \left( -\dot{m}_{evap} \right) \ dt \quad \rightarrow \quad \int\limits_{m_{sys,1}}^{m_{sys, 2}} dm_{sys} = -\int\limits_{t_1}^{t_2} \dot{m}_{evap} \ dt \quad \rightarrow \quad \Delta m_{sys} = -m_{evap} \nonumber \]
El lado izquierdo solo equivale a la acumulación de masa en el sistema y el lado derecho es la cantidad de masa transportada fuera del sistema por transferencia de masa durante el intervalo de tiempo. Así, la cantidad de masa evaporada es\[m_{evap} = -\Delta m_{sys} \quad \rightarrow \quad m_{evap} = -(-2.0 \mathrm{~kg}) = 2.0 \mathrm{~kg} \nonumber \]
Obsérvese que estas dos cantidades podrían, de hecho, computarse independientemente entre sí con las mediciones adecuadas. La conexión entre estas cantidades es la conservación de la masa para este sistema.
Para determinar la tasa promedio de evaporación, podemos revisar la forma de tiempo finito o integrada de la ecuación de conservación de masa
\[\frac{d m_{sys}}{dt} = -\dot{m}_{evap} \quad \rightarrow \quad \int\limits_{m_{sys, 1}}^{m_{sys, 2}} d m_{sys} = \underbrace{ -\int\limits_{t_1}^{t_2} \dot{m}_{evap} \ dt}_{\begin{array}{c} \text { assume mass flow } \\ \text { rate occurs at a } \\ \text{constant rate, } \dot{m}_{sys, evap} \end{array}} \quad \rightarrow \quad \Delta m_{sys} = -\dot{m}_{evap,avg} \Delta t \quad \rightarrow \quad \dot{m}_{evap, sys} = - \frac{\Delta m_{sys}}{\Delta t} \nonumber \]
Por lo tanto, la tasa promedio de evaporación es
\[\dot{m}_{evap, avg} = -\frac{\Delta m_{sys}}{\Delta t} = -\frac{(-2.0 \ \mathrm{~kg})}{(2.0 \ \mathrm{hr})} = 1.0 \ \frac{\mathrm{kg}}{\mathrm{hr}} \nonumber \]
Comentario:
¿Cambia el volumen del sistema? Si es así, ¿qué información necesitarías para poder resolver para el cambio de volumen?
¿Cómo cambiaría tu solución si usaras un sistema cerrado que consistiera en toda la acetona?
Se utiliza una jeringa hipodérmica para engrasar una parte de la máquina. El diámetro interior del tubo de jeringa de vidrio es\(1.0 \ \mathrm{cm}\) y el émbolo se mueve dentro del tubo a la velocidad de\(0.5 \ \mathrm{~cm} / \mathrm{s}\). La aguja de la jeringa tiene un diámetro interior de\(1.0 \ \mathrm{~mm}\). ¿Cuánto tiempo tardará en descargar\(12 \ \mathrm{cc}\) el aceite? ¿Cuál es la velocidad del aceite a medida que sale de la aguja? (Si es necesario, puede suponer que el aceite es incompresible y que el flujo en la aguja es unidimensional).
Solución
Conocido: Se utiliza una jeringa hipodérmica para engrasar partes.
Encuentra: Caudal volumétrico de aceite fuera de la aguja, adentro\(\mathrm{cm}^3 / \mathrm{s}\).
Tiempo requerido para la descarga\(12 \ \mathrm{cc}\) de aceite.
Velocidad del aceite que sale de la aguja, adentro\(\mathrm{cm} / \mathrm{s}\).
Dado:
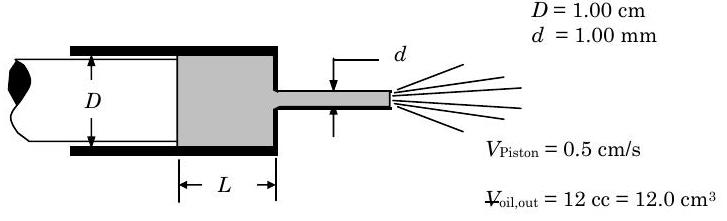
Figura\(\PageIndex{3}\): Configuración de una jeringa de aceite, con el pistón avanzando a una velocidad de\(0.5 \ \mathrm{cm/s}\).
Análisis
\(\rightarrow \quad\)Sistema de estrategia\(\rightarrow\) Volumen ocupado por el aceite dentro del cilindro y la aguja
Propiedad\(\rightarrow\) Contar la masa de petróleo, ya que el volumen está relacionado con la masa.
Intervalo de tiempo\(\rightarrow\) Tiempo finito desde la cantidad de aceite extruido dada la tasa neta.
Usando el volumen de aceite dentro del cilindro y la aguja como sistema abierto, podemos bosquejar un diagrama del sistema que muestra los caudales másticos.
Escribir la ecuación de conservación de masa para este sistema da
\[ \frac{d m_{sys}}{dt} = \underbrace{ \cancel{ \sum_{in} \dot{m}_i }^{=0} }_{\begin{array}{c} \text{no inlets assuming} \\ \text{boundary at piston moves} \end{array}} - \underbrace{ \cancel{ \sum_{out} \dot{m}_e}^{= \dot{m}_{oil, out}} }_{\begin{array}{c} \text{one outlet assuming} \\ \text{no leakage at piston} \end{array}} \quad \rightarrow \quad \frac{d m_{sys}}{dt} = - \dot{m}_{oil, out} \nonumber \]
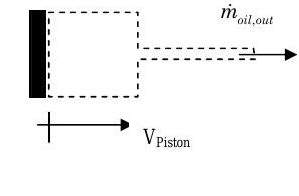
Figura\(\PageIndex{4}\): Velocidad del movimiento del pistón y caudal másico del aceite fuera del sistema.
Asumiendo densidad uniforme para el aceite da\(m_{sys}=\rho_{oil} V\kern-0.8em\raise0.3ex- _{sys}\) y\(\dot{m}_{oil, out} = \rho_{oil} \dot{ V\kern-0.8em\raise0.3ex- }_{out} \).
Sustituyendo estas relaciones de nuevo en la ecuación de conservación de masa, se convierte
\[ \frac{d m_{sys}}{d t} = -\dot{m}_{oil, out} \quad \rightarrow \quad \frac{d}{d t} \left( \rho_{oil} V\kern-0.8em\raise0.3ex- _{sys} \right) = -\rho_{oil} \dot{ V\kern-0.8em\raise0.3ex- }_{out} \quad \rightarrow \quad \cancel{ \rho_{oil} } \frac{d}{d t} \left( V\kern-0.8em\raise0.3ex- _{sys} \right) = - \cancel{ \rho_{oil} } \dot{ V\kern-0.8em\raise0.3ex- }_{out} \quad \rightarrow \quad \frac{d V\kern-0.8em\raise0.3ex- _{sys}}{d t} = -\dot{ V\kern-0.8em\raise0.3ex- }_{out} \nonumber \]
Obsérvese que para este problema en particular, parece que se conserva el volumen; sin embargo, en general no es así, o habría una ley general de conservación del volumen.
Pensando en el volumen del sistema y que el límite en el pistón se mueve con la velocidad\(V_{Piston}\), podemos representar la tasa de cambio de volumen del sistema en términos de la velocidad y área del pistón como
\[\frac{d V\kern-0.8em\raise0.3ex- _{sys} }{d t} = -A_{Piston} V_{Piston} = -\left( \frac{\pi}{4} D^{2} \right) V_{Piston} \nonumber \](¿Por qué tenemos un signo menos?)
Ahora combinando esto con el resultado de la conservación de la masa da
\[\begin{align*} \frac{d V\kern-0.8em\raise0.3ex- _{sys}}{d t} &= -\dot{ V\kern-0.8em\raise0.3ex- }_{out} \\ -\left( \frac{\pi}{4} D^{2} \right) V_{Piston} &= -\dot{ V\kern-0.8em\raise0.3ex- }_{out} \quad \rightarrow \quad \dot{ V\kern-0.8em\raise0.3ex- }_{out} = \frac{\pi}{4} D^{2} V_{Piston} = \frac{\pi}{4} \left( 1.0 \ \mathrm{~cm}^{2} \right) \left( 0.5 \ \frac{\mathrm{cm}}{\mathrm{s}} \right) = 0.393 \ \frac{\mathrm{cm}^{3}}{\mathrm{~s}} \end{align*} \nonumber \]
Ahora para encontrar el tiempo necesario para chorrear\(12.0 \ \mathrm{~cm}^{3}\), integramos la conservación del resultado masivo
\[ \frac{d V\kern-0.8em\raise0.3ex- _{sys}}{dt} = - \dot{ V\kern-0.8em\raise0.3ex- }_{out} \quad \rightarrow \quad \int\limits_{ V\kern-0.5em\raise0.3ex- _{initial}}^{ V\kern-0.5em\raise0.3ex- _{final}} dV = - \int\limits_{t_{initial}}^{t_{final}} \dot{ V\kern-0.8em\raise0.3ex- }_{out} \ dt \quad \rightarrow \quad \Delta V\kern-0.8em\raise0.3ex- _{sys} = - \dot{ V\kern-0.8em\raise0.3ex- }_{out} \Delta t \nonumber \]
\[ \Delta t = \frac{\Delta V\kern-0.8em\raise0.3ex- _{sys}}{\dot{ V\kern-0.8em\raise0.3ex- }_{sys}} = \frac{ (12.0 \ \mathrm{cm}^3) }{\left( 0.393 \ \frac{\mathrm{cm}^3}{\mathrm{s}} \right)} = 30.5 \ \mathrm{seconds} \nonumber \]
Ahora para encontrar la velocidad del aceite que sale de la aguja, podemos asumir un flujo unidimensional y usar la definición de caudal másico
\[\dot{ V\kern-0.8em\raise0.3ex- }_{out} = A_{out} V_{out} \quad \rightarrow \quad V_{out} = \frac{\dot{ V\kern-0.8em\raise0.3ex- }_{out}}{A_{out}} = \frac{\dot{ V\kern-0.8em\raise0.3ex- }_{out}}{\left( \frac{\pi}{4} D^{2} \right)} = \frac{\left( 0.393 \ \frac{\mathrm{cm}^{3}}{\mathrm{~s}} \right)}{\left( \frac{\pi}{4} \right)(0.1 \ \mathrm{~cm})^{2}}=50.0 \ \frac{\mathrm{cm}}{\mathrm{s}} \nonumber \]
Comentar
¿Podría resolver este problema con un volumen de control no deformante? [Pista: Trate el pistón que ingresa al sistema como un caudal másico. Entonces reconozca que la masa en el sistema está cambiando.]
¿Podría resolver este problema usando un sistema deformado y cerrado? [Consejo: Considere un sistema cerrado y deformante que incluya todo el aceite originalmente en el volumen del cilindro y la aguja.]
La gasolina se bombea a un tanque de almacenamiento de 1000 galones a razón de 10 gpm (galones por minuto). Durante el proceso de llenado, la gasolina se está drenando a una velocidad de 2 gpm. La entrada y el drenaje se encuentran ambos por debajo de la superficie libre de la gasolina en el tanque. ¿Cuánto tiempo tardará en llenar el tanque si inicialmente contiene 100 galones de gasolina?
Solución
Conocido: Se está llenando tanque de gasolina
Encuentra: Tiempo requerido para llenar el tanque.
Dado:
.png)
Figura\(\PageIndex{5}\): Definir el sistema y los caudales volumétricos dentro y fuera del mismo.
Análisis:
Estrategia\(\rightarrow \quad\) Sistema\(\rightarrow\) Deformar el volumen de gasolina dentro del tanque durante todo el proceso
Propiedad a Contar\(\rightarrow\) Masa del petróleo Periodo de
tiempo Tiempo\(\rightarrow\) finito
Escribiendo conservación de masa para el sistema abierto deformante que se muestra a continuación, tenemos\[\frac{d m_{sys}}{d t}=\dot{m}_{1}-\dot{m}_{2} \nonumber \]
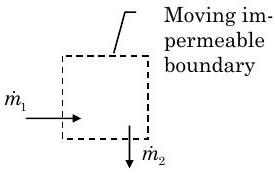
Figura\(\PageIndex{6}\): La gasolina en el tanque forma un sistema con un límite impermeable móvil.
Asumir densidad uniforme y que la gasolina es incompresible,\(\dot{m}=\rho \dot{V\kern-0.8em\raise0.3ex-}\) y\(m=\rho V\kern-0.8em\raise0.3ex-\). Sustituir estos valores de nuevo en la ecuación de conservación de masa da
\[\frac{d m_{sys}}{d t} = \dot{m}_1 - \dot{m}_2 \quad \rightarrow \quad \underbrace{ \frac{d}{d t} \left( \cancel{\rho} V\kern-0.8em\raise0.3ex-_{sys} \right) = \left( \cancel{\rho} \dot{V\kern-0.8em\raise0.3ex-}_1 \right) - \left( \cancel{\rho} \dot{V\kern-0.8em\raise0.3ex-}_2 \right) }_{\text{Density cancels out of all terms}} \quad \rightarrow \quad \frac{d V\kern-0.8em\raise0.3ex-_{sys}}{d t} = \dot{V\kern-0.8em\raise0.3ex-}_1-\dot{V\kern-0.8em\raise0.3ex-}_2 \nonumber \]
Ahora integre con el tiempo para obtener la forma de tiempo finito\[\int\limits_{t_i}^{t_f} \frac{d V\kern-0.8em\raise0.3ex-_{sys}}{d t} d t = \int\limits_{t_i}^{t_f} \left( \dot{V\kern-0.8em\raise0.3ex-}_1-\dot{V\kern-0.8em\raise0.3ex-}_2 \right) d t \quad \rightarrow \quad \Delta V\kern-0.8em\raise0.3ex- _{sys} = \underbrace{ \left(\dot{ V\kern-0.8em\raise0.3ex- }_1-\dot{ V\kern-0.8em\raise0.3ex- }_2 \right) \Delta t}_{\begin{array}{l} \text { Assumes that volumetric } \\ \text { flow rates are constant } \end{array}} \nonumber \]
Resolviendo para el intervalo de tiempo\[\Delta t = \frac{\Delta V\kern-0.8em\raise0.3ex- _{sys}}{\left( \dot{ V\kern-0.8em\raise0.3ex- }_1-\dot{ V\kern-0.8em\raise0.3ex- }_2 \right)}=\frac{(1000-100) \ \cancel{\mathrm{gal}}}{(10-2) \frac{\cancel{\mathrm{gal}}}{\mathrm{min}}}=112.5 \ \mathrm {minutes} \nonumber \]
Comentar
¿Cómo cambiaría tu respuesta si\(\dot{V\kern-0.8em\raise0.3ex-}_2 = \left(2 \frac{\text {gal}}{\text{min}}\right) \left( \frac{t}{10 \ \text{min} +t}\right) \)?
El agua fluye constantemente a través de una tubería de acero de 3 pulgadas de diámetro antes de pasar a través de un accesorio reductor a una tubería de 1 pulgada de diámetro. Todos los diámetros son diámetros internos. La velocidad promedio en la tubería más grande es de 5\(\mathrm{ft} / \mathrm{s}\). La densidad del agua es\(62.4 \mathrm{lbm} / \mathrm{ft}^{3}\). Determinar (a) el caudal másico y el caudal volumétrico en la tubería más grande, y (b) el caudal volumétrico y la velocidad promedio en la tubería más pequeña.
Solución
Conocido: El agua fluye constantemente a través de un accesorio reductor
Encuentra: Caudal volumétrico y másico en la tubería de 3 pulgadas. Caudal volumétrico y velocidad promedio en tubería de 1 pulgada.
Dado:
.png)
Figura\(\PageIndex{7}\): Definir el sistema como el agua dentro del reductor.
\(\rightarrow \quad \)Sistema de estrategia — Sistema abierto no deformante como se muestra en la figura para relacionar los flujos en la entrada y salida.
Propiedad a contar — Masa porque tenemos que relacionar flujos en dos ubicaciones Periodo de
tiempo — Problema de estado estacionario ya que dado solo tasas.
Escribir la ecuación de conservación de masa para este sistema abierto da
\[ \underbrace{ \cancel{ \frac{d m_{sys}}{dt} }^{=0} }_{\begin{array}{c} \text {steady-state} \\ \text {conditions} \end{array}} =\dot{m}_{1}-\dot{m}_{2} \quad \rightarrow \quad \dot{m}_{2}=\dot{m}_{1} \nonumber \]
A partir de la definición de velocidad media\(\dot{m}=\rho A_{c} V_{\text {avg }}\) y\(\dot{V\kern-0.8em\raise0.3ex-}=A_{c} V_{\text {avg }}\) podemos resolver para la información solicitada en la Entrada 1:
\[\begin{align*} &\dot{V\kern-0.8em\raise0.3ex-}_{1} = A_{c, 1} V_{avg, 1} = \left( \frac{\pi}{4} D_{1}^{2}\right) V_{avg, 1} = \left[ \frac{\pi}{4} \left(\frac{3.00}{12} \ \mathrm{ft}\right)^{2}\right] (5.00 \ \mathrm{ft} / \mathrm{s}) = 0.245 \ \frac{\mathrm{ft}^{3}}{\mathrm{~s}} \\ &\dot{m}_{1} = \rho \dot{V\kern-0.8em\raise0.3ex-}_{1} = \left(62.4 \ \frac{\mathrm{lbm}}{\mathrm{ft}^{3}}\right)\left(0.245 \ \frac{\mathrm{ft}^{3}}{\mathrm{~s}}\right) = 15.3 \ \frac{\mathrm{lbm}}{\mathrm{s}} \end{align*} \nonumber \]
Ahora en Outlet 2 podemos hacer uso de la conservación de los resultados de masa desde arriba. Suponiendo que la densidad es uniforme, entonces
\[\dot{m}_{2} = \dot{m}_{1} \quad \rightarrow \quad \cancel{ \rho } \dot{V\kern-0.8em\raise0.3ex-}_{2} = \cancel{ \rho } \dot{V\kern-0.8em\raise0.3ex-}_{1} \quad \rightarrow \quad \dot{V\kern-0.8em\raise0.3ex-}_{2} = 0.245 \ \frac{\mathrm{ft}^{3}}{\mathrm{~s}} \nonumber \]
Para encontrar la velocidad\[\begin{align*} &\dot{V\kern-0.8em\raise0.3ex-}_{2}=\dot{V\kern-0.8em\raise0.3ex-}_{1} \quad \rightarrow \quad A_{c, 2} V_{avg, 2}=A_{c, 2} V_{c, 1} \quad \rightarrow \quad V_{avg, 2}=\frac{A_{c, 1}}{A_{c, 2}} V_{c, 1} \\ &V_{avg, 2} = \frac{\left(\dfrac{\pi}{4} D_{1}^{2}\right)}{\left(\dfrac{\pi}{4} D_{2}^{2}\right)} V_{avg, 1}=\left(\frac{D_{1}}{D_{2}}\right)^{2} V_{avg, 1}=\left(\frac{3}{1}\right)^{2} \left(5 \ \frac{\mathrm{ft}}{\mathrm{s}}\right) = 45.0 \ \frac{\mathrm{ft}}{\mathrm{s}} \end{align*} \nonumber \]
Considere el tanque de agua que se muestra a continuación. El tanque se puede llenar usando el grifo en la parte superior o la entrada en la parte inferior del tanque. El piso del tanque tiene un área de\(A_{\text {tank }}=10 \mathrm{~m}^{2}\), y las paredes del tanque son verticales.
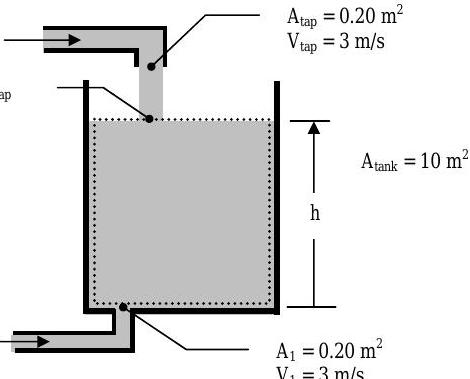
Figura\(\PageIndex{8}\): Definir el sistema y las dos entradas que conducen al mismo.
La pregunta que nos ocupa es, ¿cuánto tiempo tardará en elevar el nivel\(h\) del agua de 2 metros a 5 metros si lleno el tanque con la entrada en el fondo del tanque? ¿Qué pasa si uso el grifo en la parte superior del tanque? ¿Hará alguna diferencia?
Llenar el tanque desde la entrada en el piso del tanque
Para fines de este análisis, debemos seleccionar un sistema, cosas a contar y un periodo de tiempo:
Sistema\(\rightarrow\) Escoge el volumen del agua dentro del tanque. (Ver las líneas discontinuas en la figura anterior. La masa puede fluir hacia este volumen en 1 y el límite superior del tanque, que corresponde con la superficie libre del agua en el tanque, se mueve hacia arriba y hacia abajo con el agua. Llamar a este Sistema I.)
Cosas para contar\(\rightarrow\) Masa de agua dentro del sistema
Período de tiempo\(\rightarrow\) Dado que se nos pide encontrar la cantidad de tiempo eventualmente necesitaremos un análisis de tiempo finito. (Sin embargo, mi experiencia, que estoy compartiendo con ustedes, me dice que es más fácil comenzar con la forma de tarifa (periodo de tiempo infinitesimal) y luego integrarse para obtener la forma de tiempo finito).
La aplicación de la ecuación de conservación de masa a este sistema da lo siguiente:
\[ \frac{d m_{sys}}{dt} = \dot{m}_1 \nonumber \]
Ahora para introducir el nivel o profundidad del agua en el problema, debemos considerar cómo se relaciona la masa del sistema con la profundidad del agua. La aplicación de la ecuación fundamental para calcular la masa dentro de un sistema da el siguiente resultado:
\[ m_{sys} = \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} \rho \ d V\kern-0.8em\raise0.3ex- = \underbrace{ \rho \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} d V\kern-0.8em\raise0.3ex- }_{\begin{array}{c} \text {Assume} \\ \text {uniform} \\ \text{density} \end{array}} = \rho V\kern-0.8em\raise0.3ex-_{sys} = \underbrace{ \rho A_{\text{tank}} h }_{\text{Since} V\kern-0.5em\raise0.3ex-_{sys} = A_{\text{tank}} h} \nonumber \]
De igual manera, necesitamos determinar el caudal másico a 1 en términos de la información conocida de la siguiente manera:
\[\dot{m}_{1} = \int\limits_{A_1} \rho V_{\text{n, rel}} \ dA = \underbrace{\rho_{1} \int_{A_1} V_{\text {n, rel}} \ dA}_{\begin{array}{c} \text { Uniform density} \\ \text {at the inlet} \end{array}} = \underbrace{\rho_1 V_1 \int\limits_{A_1} dA}_{\begin{array}{c} \text { Uniform velocity } \\ V_1=V_{\text{n, rel}} \end{array}} = \rho_{1} V_{1} A_{1} \nonumber \]
Ahora podemos volver a combinar toda esta información en la conservación de la ecuación de masa Eq. \(\PageIndex{2}\)de la siguiente manera:
\[\begin{align} \frac{d m_{sys}}{d t} &=\dot{m}_{1} \nonumber \\ \frac{d}{d t} \left( \rho A_{\text {tank}} h \right) &= \rho_{1} A_{1} V_{1} \end{align} \nonumber \]
Suponiendo que el agua es incompresible, entonces la densidad del agua en el sistema\(\rho\) y la densidad del agua que ingresa al sistema\(\rho_{1}\) son iguales y la ecuación de conservación de masa se reduce (como se desarrolla en la Ec. \(\PageIndex{5}\)) a
\[\begin{align} A_{\mathrm{tank}} \frac{d h}{d t} &=A_{1} V_{1} \nonumber \\ \frac{d h}{d t} &=\frac{A_{1}}{A_{\mathrm{tank}}} V_{1} \end{align} \nonumber \]
Integrando esta ecuación para\(h\) encontrar el tiempo que tarda en pasar de 2 a 5 metros, usaremos una integral definida entre límites especificados\[\begin{gather} \int d h = \int\left(\frac{A_1}{A_{\text{tank}}} V_1\right) dt = \left( \frac{A_1}{A_{\text{tank}}} V_1 \right) \int dt \quad \rightarrow \quad \int\limits_{h_1}^{h_2} dh=\int_{t_1}^{t_2} \left( \frac{A_1}{A_{\text{tank}}} V_1 \right) dt = \left(\frac{A_1}{A_{\text{tank}}} V_1 \right) \int\limits_{t_1}^{t_2} dt \nonumber \\ h_{2}-h_{1}=\left(\frac{A_{1}}{A_{\text {tank }}} V_{1}\right)\left(t_{2}-t_{1}\right) \end{gather} \nonumber \]
Ahora resolviendo para la respuesta numérica que tenemos
\[ \Delta t = t_2 - t_1 = \frac{\left( h_2 - h_1 \right) }{\left( \frac{A_1}{A_{\text{tank}} V_1} \right)} = \frac{(5-2) \ \mathrm{m}}{\left( \frac{0.2 \ \mathrm{m}^2}{10 \ \mathrm{m}^2} \right) \left( 3 \ \frac{\mathrm{m}}{\mathrm{s}} \right)} = 50 \ \mathrm{s} \nonumber \]
Llenar el tanque desde el grifo en la parte superior del tanque
Para fines de este análisis, debemos seleccionar un sistema, cosas a contar y un periodo de tiempo:
Sistema\(\rightarrow\) Escoge el volumen del agua dentro del tanque. (Vea las líneas discontinuas en la figura a continuación.) La masa puede fluir hacia este volumen a 2, que es parte del límite superior del sistema. Además, todo el límite superior del tanque, que corresponde con la superficie libre del agua en el tanque, se mueve hacia arriba y hacia abajo con el agua. Llama a este Sistema II.
.png)
Figura\(\PageIndex{9}\): Definir el sistema y las dos entradas que conducen al mismo.
Cosas para contar\(\rightarrow\) Masa de agua dentro del sistema
Período de tiempo\(\rightarrow\) Dado que se nos pide encontrar la cantidad de tiempo, eventualmente necesitaremos un análisis de tiempo finito. (Sin embargo, mi experiencia, que estoy compartiendo con ustedes, me dice que es más fácil comenzar con la forma de tarifa (periodo de tiempo infinitesimal) y luego integrarse para obtener la forma de tiempo finito).
Antes de continuar asegúrate de entender la diferencia entre el sistema seleccionado aquí (Sistema II) y el utilizado anteriormente (Sistema I). Esto es muy importante.
Considera las preguntas:
- ¿Qué hay dentro de cada sistema?
- ¿Ambos son sistemas abiertos?
- ¿Qué límites tienen flujo?
- ¿Qué límites se mueven?
- ¿Cómo esperarías que la forma de cada sistema cambiara con el tiempo?
La aplicación de la ecuación de conservación de masa al Sistema II da lo siguiente:
\[ \frac{d m_{sys}}{dt} = \dot{m}_2 \nonumber \]
Ahora para introducir el nivel o profundidad del agua en el problema, debemos considerar cómo se relaciona la masa del sistema con la profundidad del agua. La aplicación de la ecuación fundamental para calcular la masa dentro de un sistema da el siguiente resultado:
\[ m_{sys} = \int\limits_{V\kern-0.5em\raise0.3ex-_{sys}} \rho \ d V\kern-0.8em\raise0.3ex- = \underbrace{ \rho \int\limits_{V\kern-0.5em\raise0.3ex-} d V\kern-0.8em\raise0.3ex- }_{\begin{array}{c} \text {Assume} \\ \text{uniform} \\ \text{density} \end{array}} = \rho V\kern-0.8em\raise0.3ex- = \underbrace{ \rho A_{\text{tank}} h }_{\text{Since } V\kern-0.5em\raise0.3ex-_{sys} = A_{\text{tank}} h} \nonumber \]
De igual manera necesitamos determinar el caudal másico en la entrada 2 en términos de la información conocida de la siguiente manera:
\[ \dot{m}_2 = \int\limits_{A_2} \rho V_{\text{n, rel}} \ dA = \underbrace{ \rho_2 \int\limits_{A_2} V_{\text{n, rel}} \ dA }_{\begin{array}{c} \text{Uniform density} \\ \text{at the inlet} \end{array}} = \underbrace{ \rho_2 V_{\text{2, rel}} \int\limits_{A_2} dA }_{\begin{array}{c} \text {Uniform density} \\ V_{2, rel} = V_{n, rel} \end{array}} = \rho_2 V_{\text{2, rel}} dA = \rho V_{\text{2, rel}} A_2 \nonumber \]
En este punto debemos tener mucho cuidado para calcular correctamente la velocidad de la masa que cruza el límite del sistema. Recordemos que el caudal másico se define con respecto a algún límite. Por ejemplo, el caudal másico del agua que sale del grifo, es decir, cruzando el plano de salida del grifo, es\(\dot{m}_{tap} = \rho A_{tap} V_{tap}\). Esto supone que la densidad y la velocidad son uniformes en la sección transversal del flujo y que la velocidad\(\mathbf{V_{tap}}\) se mide con respecto al plano de salida del grifo.
Ahora, para calcular el caudal másico a 2 en el límite de nuestro sistema requiere que sepamos la velocidad del agua en relación con el límite del sistema que se está moviendo.
.jpg)
Figura\(\PageIndex{10}\): Tasa de cambio del límite superior del sistema.
Refiriéndose a la figura, vemos que con respecto al suelo (o cualquier otro punto estacionario) la velocidad del chorro\(V_{tap}\) y la velocidad del límite se\(V_{boundary}\) pueden esbozar en la figura. La posición del límite (la superficie libre del agua) se puede definir en términos de la altura de la superficie\(h\) medida desde el fondo del tanque. La velocidad del límite con respecto al fondo del tanque (un punto estacionario) se puede definir como\(V_{boundary} = dh/dt\).
Para calcular la velocidad relativa del fluido que ingresa al sistema medida con respecto al límite móvil debemos recurrir a las relaciones físicas básicas para los cálculos de velocidad relativa:
Dado el objeto que se\(A\) mueve con la velocidad\(V_A\) medida con respecto a un punto estacionario\(O\) y el objeto que se\(B\) mueve con la velocidad\(V_B\) medida con respecto al mismo punto estacionario\(O\), entonces
la velocidad relativa de\(A\) con respecto a\(B\) es\( \mathbf{V}_{A/B} = \mathbf{V}_A – \mathbf{V}_B\) y
la velocidad relativa de\(B\) con respecto a\(A\) es\(\mathbf{V}_{B/A} = \mathbf{V}_B – \mathbf{V}_A\).
Aplicando este resultado a nuestro problema anterior da el resultado de que
\[ \begin{align} \mathbf{V}_{2, \text{rel}} &= \mathbf{ V _{tap/boundary} } \nonumber \\ &= \mathbf{V}_{\text{tap}} - \mathbf{V}_{\text{boundary}} \nonumber \\ V_{2, \text{rel}} \mathbf{i}_{\text{in}} &= V_{\text{tap}} \mathbf{i}_{\text{in}} - \left( - V_{\text{boundary}} \mathbf{i}_{\text{in}} \right) \\ &= \left( V_{\text{tap}} + V_{\text{boundary}} \right) \mathbf{i}_{\text{in}} \nonumber \\ V_{2, \text{rel}} &= V_{\text{tap}} + V_{\text{boundary}} = V_{\text{tap}} + \frac{dh}{dt} \nonumber \end{align} \nonumber \]
donde\(\mathbf{i}_{\text{in}}\) es un vector unitario apuntando hacia el sistema (vea la figura anterior del límite móvil).
Tenga en cuenta que Ec. \(\PageIndex{12}\)tiene sentido físico. El límite del sistema y el agua entrante se mueven uno hacia el otro; por lo tanto, aumentar la velocidad del grifo o aumentar la velocidad de cambio de ambos\(h\) aumentará la velocidad relativa del agua que cruza el límite del sistema medida con respecto al límite móvil.
Ahora la combinación de estos resultados con la ecuación de conservación de masa da\[\frac{d m_{\mathrm{sys}}}{d t}=\dot{m}_{2} \quad \rightarrow \quad \frac{d}{dt} \left( \rho A_{\mathrm{tank}} h \right) = \rho_{2} A_{2} V_{2, \mathrm{rel}} \quad \rightarrow \quad \frac{d}{dt} \left( \rho A_{\mathrm{tank}} h \right) = \rho_{2} A_{2} \left( V_{\mathrm{tap}} + \frac{d h}{d t} \right) \nonumber \]
De nuevo asumiendo que el agua es una sustancia incompresible y también asumiendo que la zona nos\(A_{2}=A_{\text {tap }}{ }^{1}\) da el siguiente resultado:
\[\begin{gather} \frac{d}{d t}\left(\rho A_{\text {tank }} h\right)=\rho_{2} A_{2}\left(V_{\text {tap }}+\frac{d h}{d t}\right) \quad \rightarrow \quad \rho A_{\text {tank }} \frac{d h}{d t}=\rho_{2} A_{2}\left(V_{\text {tap }}+\frac{d h}{d t}\right) \nonumber \\ \left(A_{\text {tank }}-A_{2}\right) \frac{d h}{d t}=A_{2} V_{\text {tap }} \nonumber \\ \frac{d h}{d t}=\left(\frac{A_{2}}{A_{\text {tank }}-A_{2}}\right) V_{\text {tap }} \end{gather} \nonumber \]
Integrando la Ec. \(\PageIndex{14}\)como antes obtengamos:
\[h_{2} - h_{1} = \left( \frac{A_2}}{A_{\text {tank}}-A_2} \right) V_{\text {tap}} \left( t_2-t_1 \right) \nonumber \]
Y resolviendo para las respuestas numéricas, obtenemos
\[\Delta t = t_2 -t_1 = \frac{ \left( h_2-h_1 \right) }{\left[ \left(\frac{A_2}{A_{\text {tank}}-A_2} \right) V_{\text {tap}} \right]}=\frac{(5-2) \ \mathrm{m}}{\left[ \left( \frac{0.2 \ \mathrm{~m}^{2}}{(10-0.2) \ \mathrm{m}^{2}} \right) \left( 3 \ \frac{\mathrm{m}}{\mathrm{s}} \right) \right]}=49 \ \mathrm{~s} \nonumber \]
Nota: Debe tener en cuenta que la suposición que\(A_{2}=A_{\text {tap}}\) está directamente relacionada con nuestra suposición de que la velocidad absoluta del chorro de agua del grifo en el límite es la misma que la velocidad del agua que sale del grifo\(V_{\text {tap}}\)
Comparando los resultados
¿Qué arreglo “llena” el tanque más rápido? ¿Esto te parece extraño?
¿Cómo cambiaría la comparación si\(A_{\text{tap}} = A_1 = 1 \ \mathrm{m}^2\)? ¿El Sistema II seguiría siendo más rápido?
- Sistema I:
- Sistema II:
Supongamos que empecé con un tanque vacío. ¿Siempre tomará menos tiempo “llenar” el tanque si uso un grifo?


