3.5: Contabilidad de Especies Químicas

Para muchos problemas, es esencial realizar un seguimiento de las especies químicas individuales, átomos o moléculas. Ejemplos de estos incluyen

• procesos de combustión, por ejemplo, quemar gasolina en el aire
• procesos de mezcla, por ejemplo, mezcla de agua y anticongelante
• cualquier proceso con reacciones químicas
• preparación de soluciones sólidas, por ejemplo, cristal de silicio dopado

Aunque la masa total siempre se conserva, no existe tal ley de conservación para las especies químicas en general.

Experimentando con Conservación de Masa

Para ver qué sucede cuando tratamos de dar cuenta de especies químicas individuales, considere el reactor químico de estado estacionario en la Figura\(\PageIndex{1}\). El compuesto\(A\) y el compuesto\(B\) fluyen al reactor y se combinan para producir el compuesto\(C\).

Figura\(\PageIndex{1}\): Reactor químico de estado estacionario

Escribir la forma de velocidad de la ecuación de conservación de masa da\[\frac{d m_{s y s}}{d t}=\dot{m}_1 + \dot{m}_2 - \dot{m}_3. \nonumber \] Para la operación en estado estacionario la tasa de cambio de masa dentro del sistema es cero. Reorganizar y resolver para el caudal másico en la salida da\[\dot{m}_3 = \dot{m}_1 + \dot{m}_2. \nonumber \] Ahora intentemos escribir una ecuación similar para solo compuesto\(C\). Comenzando con la conservación de la ecuación de masa para solo compuesto\(C\) tenemos

\[ \underbrace{ \frac{dm_{C,sys}}{dt} }_{\begin{array}{c} \text {Rate of change} \\ \text {of compound } C \\ \text {inside the system} \end{array}} = \underbrace{ \dot{m}_{C, 1} + \dot{m}_{C, 2} }_{\begin{array}{c} \text {Mass flow rate} \\ \text {of compound } C \\ \text {entering the system} \end{array}} - \underbrace{ \dot{m}_{C, 3} }_{\begin{array}{c} \text {Mass flow rate} \\ \text {of compound } C \\ \text {leaving the system} \end{array}} \nonumber \]

Por definición, para un sistema de estado estacionario las propiedades intensivas y extensas del sistema son independientes del tiempo. Por lo tanto, el plazo de tasa de cambio debe ser cero. También sabemos por nuestra declaración de problemas que solo compuestos\(A\) e\(B\) ingresan al sistema; así, los caudales másico de\(C\) en las entradas 1 y 2 son idénticamente cero. Armar esto da el siguiente resultado:\[0=0 + 0 - \dot{m}_{C, 3} \nonumber \] Este resultado es inconsistente con nuestra comprensión de la situación física. Sabemos que el compuesto\(C\) está saliendo de nuestro reactor de estado estacionario. ¿De dónde viene? Unos momentos de reflexión podrían sugerir que nuestra experiencia nos dice que el compuesto\(C\) se está generando dentro del sistema.

Si intentáramos escribir ecuaciones similares para compuestos\(A\) y compuestos\(B\), se nos ocurriría el mismo resultado físicamente inconsistente. En este caso, podríamos concluir que el compuesto\(A\) y el compuesto\(B\) se están consumiendo dentro de este sistema.

Para remediar esta inconsistencia intentemos modificar nuestro balance de masas para dar cuenta de la generación y consumo de especies químicas individuales. Para nuestro reactor químico particular, la ecuación podría verse así para el compuesto\(i\):

\[\underbrace{ \frac{d m_{i, sys}}{d t} }_{\begin{array}{c} \text {Rate of accumulation} \\ \text {of compound } i \\ \text {inside the system} \end{array}} = \underbrace{ \dot{m}_{i, 1} + \dot{m}_{i, 2} - \dot{m}_{i, 3}} _ {\begin{array}{c} \text {Transport rate of} \\ \text {compound } i \\ \text {across the} \\ \text {system boundary} \end{array}} + \underbrace{ \dot{m}_{i, \text { gen}}} _ {\begin{array}{c} \text {Generation rate} \\ \text {of compound } i \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{i, \text { cons}}} _ {\begin{array}{c} \text {Consumption rate} \\ \text {of compound } i \\ \text {inside the system} \end{array}} \nonumber \]

Escribir esta ecuación para cada uno de los tres compuestos en nuestro reactor químico sujeto a los supuestos apropiados, por ejemplo, operación en estado estacionario y compuestos puros en los tres límites de flujo, da

\[\begin{array}{ll} \text { Compound } A: & 0=\dot{m}_{A, 1} - 0 + 0 - \dot{m}_{A, \text { cons }} \\ \text { Compound } B: & 0=\dot{m}_{B, 1} - 0 + 0 - \dot{m}_{B, \text { cons }} \\ \text { Compound } C: & 0=0-\dot{m}_{C, 3} + \dot{m}_{C, \text{ gen}} - 0 \end{array} \nonumber \]

Si sumamos estas tres ecuaciones obtenemos la siguiente relación:\[0 = \underbrace{ \left[ \dot{m}_{A, 1} + \dot{m}_{B, 2} - \dot{m}_{C, 3} \right] }_{ =0 \atop \begin{array}{c} \text {From conservation} \\ \text {of total mass} \end{array}} + \left[ \dot{m}_{C, \text{ gen}} - \dot{m}_{A, \text { cons}}-\dot{m}_{B, \text { cons}} \right] \nonumber \] Dado que los términos en los primeros paréntesis del lado derecho satisfacen la conservación de la ecuación de masa total escrita anteriormente, nos quedamos con la conclusión de que los términos en el segundo conjunto de paréntesis deben satisfacer lo siguiente relación:

\[ \underbrace{ \dot{m}_{C, \text{ gen}} }_{\begin{array}{c} \text {Generation rate} \\ \text {of compound } C \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{A, \text{ cons}} }_{\begin{array}{c} \text {Consumption rate} \\ \text {of compound } A \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{B, \text{ cons}} }_{\begin{array}{c} \text {Consumption rate} \\ \text {of compound } B \\ \text {inside the system} \end{array}} = 0 \nonumber \]

Al examinar este resultado, parecería que esta relación es consecuencia directa del hecho empírico de que se conserva la masa total. En la siguiente sección escribiremos un estado contable general para cualquier especie química en términos tanto de la masa de la especie como del número de moles de la especie.

Ecuación contable para especies químicas

A partir de los resultados de la última sección y nuestra experiencia con el marco contable, podemos escribir dos ecuaciones contables o de balance diferentes para cualquier especie química individual.

Base de masa para compuesto\(i\)

Sobre una base de masa, la ecuación contable se escribe en términos de la masa del sistema, los caudales másticos y la generación y consumo de masa del compuesto especificado:

\[\underbrace{ \frac{d m_{i, sys}}{d t} }_{\begin{array}{c} \text {Rate of accumulation} \\ \text { of mass } \\ \text {of Compound } i \\ \text {inside the system} \end{array}} = \underbrace{ \left[ \sum_{in} \dot{m}_{i, i} - \sum_{out} \dot{m}_{i, e} \right] }_{\begin{array}{c} \text {Net flow rate} \\ \text {of mass} \\ \text {of Compound } i \\ \text {into the system} \end{array}} + \underbrace{ \left[ \dot{m}_{i, gen} - \dot{m}_{i, cons} \right] }_{\begin{array}{c} \text {Net generation rate} \\ \text {of mass} \\ \text{of Compound } i \\ \text {inside the system} \end{array}} \nonumber \]donde\[\begin{aligned} m_{i, sys} &= \int_{V_{sys}} \rho_{i} \ dV, \text {the mass of } i \text{ inside the system }(\mathrm{kg}) \\ \dot{m}_{i, i} ; \, \dot{m}_{i, e} &=\text {mass flow rate of } i \text{ into or out of the system }(\mathrm{kg} / \mathrm{s}) \\ \dot{m}_{i, gen} ; \, \dot{m}_{i, cons} &=\text {generation/consumption rate of } i \text{ inside the system }(\mathrm{kg} / \mathrm{s}) \end{aligned} \nonumber \]

Tenga en cuenta que los términos de generación y consumo son cada uno idénticos cero a menos que existan reacciones químicas en el sistema.

Base molar para el compuesto\(i\)

Sobre una base molar, la ecuación contable se escribe en términos de los moles del sistema, caudales molares, y generación y consumo de moles del compuesto especificado:\[\underbrace{ \frac{d n_{i, sys}}{dt} }_{\begin{array}{c} \text {Rate of Accumulation} \\ \text {of moles} \\ \text {of Compound } i \\ \text {inside the system} \end{array}} = \underbrace{\left[ \sum_{in} \dot{n}_{i, i} - \sum_{out} \dot{n}_{i, e} \right] }_{\begin{array}{c} \text {Net molar flow rate} \\ \text {of Compound } i \\ \text {into the system} \end{array}} + \underbrace{ \left[ \dot{n}_{i, gen} - \dot{n}_{i, cons} \right] }_{\begin{array}{c} \text {Net generation rate} \\ \text {of moles} \\ \text {of Compound } i \\ \text {inside the system} \end{array}} \nonumber \] donde\[\begin{aligned} n_{i, sys} &=\int_{V_{sys}} \bar{\rho}_{i} \ dV, \text { the number of moles of} i \text{ inside the system (kmol) } \\ \bar{\rho}_{i} &=\text {molar density of } i \left(\mathrm{kmol} / \mathrm{m}^{3}\right) \\ \dot{n}_{i, i} ; \, \dot{n}_{i, e}&=\text {molar flow rate of } i \text{ into or out of the system }(\mathrm{kmol} / \mathrm{s}) \\ \dot{n}_{i, gen} ; \, \dot{n}_{i, cons}&=\text {generation/consumption rate of moles of } i \text { inside the system } (\mathrm{kmol} / \mathrm{s}) \end{aligned} \nonumber \] De nuevo, al igual que con la ecuación de base de masa, los términos de generación y consumo son cada uno idénticamente cero a menos que existan reacciones químicas en el sistema.

Aplicación de Contabilidad de Especies Químicas

Hay dos clases amplias de problemas en los que la contabilidad de especies químicas es importante:

• Sistemas sin reacciones químicas, y
• Sistemas con reacciones químicas.

Sistemas sin reacciones químicas

Si un sistema no tiene reacciones químicas, lo primero que hay que reconocer es que tanto la tasa de generación como los términos de tasa de consumo para cualquier compuesto son idénticamente cero.

• Si la composición química para el sistema también es constante (con el tiempo) y uniforme (en el espacio), las ecuaciones contables de especies duplican la conservación de las ecuaciones de masa y no agregan nada a nuestro análisis.
• Si la composición química también depende del tiempo y no es uniforme, las ecuaciones contables de especies pueden proporcionar información adicional que complemente la conservación de las ecuaciones de masa. Ejemplos de esto incluyen problemas relacionados con la mezcla, separación y destilación.

Al aplicar tanto la conservación de la masa como las ecuaciones contables de especies, es importante reconocer cuántas ecuaciones independientes se pueden escribir para un sistema específico.

Para cualquier sistema no reactivo, el número máximo de ecuaciones independientes que se pueden obtener aplicando la conservación de la masa total y la contabilidad de especies es igual al número de especies independientes involucradas en el proceso

Ponte a prueba

Intente decidir cuántas ecuaciones independientes se pueden escribir para los siguientes sistemas de estado estacionario:

(a) T en un conducto de aire

• Entrada-1\(\quad\) Aire
• Outlet-2\(\quad\) Aire
• Outlet-3\(\quad\) Aire

b) Proceso de separación de aire

• Inlet-1\(\quad\) Aire compuesto por\(79 \% \mathrm{~N}_{2}\) y\(21 \% \mathrm{O}_{2}\) (análisis molar)
• Outlet-2\(\quad\) Pure\(\mathrm{O}_{2}\)
• Outlet-3\(\quad\) Pure\(\mathrm{N}_{2}\)

(c) Humidificador

• Entrada-1\(\quad\) Aire
• Entrada-2 Vapor de\(\quad\) agua
• Outlet-3 Mezcla de vapor\(\quad\) de aire-agua

(d) Cámara de mezcla

• Entrada-1 Vapor de agua\(\left(\mathrm{H}_{2} \mathrm{O}\right)\)
• Entrada-2 Dióxido\(\quad\) de carbono\(\left(\mathrm{CO}_{2}\right)\)
• Inlet-3 Aire compuesto por\(79 \% \mathrm{~N}_{2}\) y\(21 \% \mathrm{O}_{2}\) (análisis molar)
• Outlet-4 Mezcla gaseosa de\(\mathrm{H}_{2} \mathrm{O}, \, \mathrm{CO}_{2}, \, \mathrm{N}_{2}\),\) y\(\mathrm{O}_{2}\)

e) Proceso de destilación

• Entrada-1: Mezcla\(\quad\) agua-alcohol con composición 1
• Outlet-2: Mezcla\(\quad\) agua-alcohol con composición 2
• Outlet-3: Mezcla\(\quad\) agua-alcohol con composición 3

Los siguientes dos ejemplos demuestran cómo utilizar las ecuaciones contables de especies para resolver problemas que no involucren reacciones químicas.

Contabilidad de Especies — Problemas sin Reacción Química

Los problemas con el cambio de composición se pueden separar en dos grupos: sistemas con reacción química y sistemas sin reacción química. El enfoque de esta subsección son los sistemas sin reacción química.

Ecuaciones contables de especies

Para sistemas sin reacción química, las ecuaciones contables de especies pueden escribirse sin los términos de generación/consumo. En términos de la masa de componente\(j\), la ecuación contable de especies se convierte en

\[\frac{d m_{j, sys}}{d t} = \sum_{in} \dot{m}_{j, i} - \sum_{out} \dot{m}_{j, e} + \cancel {\dot{m}_{j, gen}}^{=0} - \cancel {\dot{m}_{j, cons}}^{=0} \quad \rightarrow \quad \frac{d m_{j, sys}}{d t} = \sum_{in} \dot{m}_{j, i} - \sum_{out} \dot{m}_{j, e} \nonumber \]y en términos de la cantidad de sustancia\(j\) (moles de componente\(j\)) la ecuación contable de especies se convierte

\[\frac{d n_{j, sys}}{d t} = \sum_{in} \dot{n}_{j, i} - \sum_{out} \dot{n}_{j, e} + \cancel{\dot{n}_{j, gen}}^{=0} - \cancel{\dot{n}_{j, cons}}^{=0} \quad \rightarrow \quad \frac{d n_{j, sys}}{d t} = \sum_{in} \dot{n}_{j, i} - \sum_{out} \dot{n}_{j, e} \nonumber \]

Estas ecuaciones se pueden escribir para realizar un seguimiento de cualquier componente químico al estudiar el comportamiento de un sistema con composición cambiante y sin reacciones químicas. Ejemplos de este tipo de problemas involucran los procesos físicos de mezcla, separación y destilación.

Dado un sistema con compuestos\(N_{\text {comp}}\) químicos, se puede escribir un total de\(N_{\text {comp}}+1\) ecuaciones aplicando la conservación de la masa total\(m\) y aplicando especies que contabilizan cada uno de los\(N_{\text {comp}}\) compuestos. Desafortunadamente, sólo\(N_{\text {comp}}\) de estas ecuaciones son independientes. (Esto significa que cualquiera\(N_{\text {comp}}\) de las\(N_{\text {comp }}+1\) ecuaciones disponibles anteriormente se puede combinar por álgebra simple para recuperar la ecuación restante).

Ecuaciones de composición

La composición de la mezcla siempre se puede describir en términos de las fracciones de masa y fracciones molares. Para cualquier sistema, se puede escribir una ecuación de composición para cada flujo de flujo, y se puede escribir una ecuación de composición adicional para describir el contenido del sistema. Para un sistema de estado estacionario, la ecuación de composición del sistema es innecesaria.

Considere un sistema abierto con tres componentes\(A,\)\(B\), y\(C\). Para cada corriente de entrada o salida, digamos corriente 1, podemos relacionar el caudal másico (o molar) de cada componente con el caudal total en la entrada o salida como se muestra a continuación:\[\begin{array}{llll} \dot{m}_1 = \dot{m}_{A, 1} + \dot{m}_{B, 1} + \dot{m}_{C, 1} &= m f_{A, 1} \dot{m}_{1} + m f_{B, 1} \dot{m}_{1} + m f_{C, 1} \dot{m} & \rightarrow & 1=m f_{A, 1} + m f_{B, 1} + m f_{C, 1} \\ \dot{n}_1 = \dot{n}_{A, 1} + \dot{n}_{B, 1} + \dot{n}_{C, 1} &= n f_{A, 1} \dot{n}_{1} + n f_{B, 1} \dot{n}_{1} + n f_{C, 1} \dot{n}_{1} & \rightarrow & 1 = n f_{A, 1} + n f_{B, 1} + n f_{C, 1} \end{array} \nonumber \] Para el contenido del sistema, la masa o cantidad de sustancia (moles) para cada componente puede escribirse como se muestra a continuación:

\[\begin{array} m_{sys} &= m_{A, sys} + m_{B, sys} + m_{C, sys} \\ &= m f_{A, sys} m_{sys} + m f_{B, sys} m_{sys} + m f_{C, sys} m_{sys} \quad \rightarrow \quad &1 = mf_{A, sys} + mf_{B, sys} + mf_{C, sys} \\ n_{sys} &= n_{A, sys} + n_{B, sys} + n_{C, sys} \\ &=n f_{A, sys} n_{sys} + n f_{B, sys} n_{sys} + n f_{C, sys} n_{sys} \quad \rightarrow \quad &1 = nf_{A, sys} + nf_{B, sys} + nf_{C, sys} \end{array} \nonumber \]

Ejemplo: problema de mezcla

Un proceso químico específico requiere una mezcla de metanol, etanol y agua a un caudal másico de\(200 \mathrm{~kg} / \mathrm{h}\). La corriente de producto se forma mediante el uso de dos corrientes que contienen cada una solo dos componentes. La información conocida sobre los caudales y la composición para este problema de mezcla en estado estacionario se muestra en la tabla.

Utilizando la información de la tabla y cualquier suposición adicional, determinar las composiciones y caudales desconocidos. [Nota: No se producen reacciones químicas.]

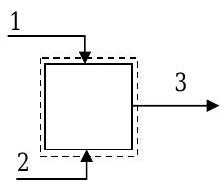
Figura\(\PageIndex{2}\): Configuración del sistema para el problema de mezcla.

Stream	Caudal másico	Composición — Masa%
		Metanol	Etanol	Agua
1			0
2	\(120 \mathrm{~kg} / \mathrm{h}\)	0
3	\(200 \mathrm{~kg} / \mathrm{h}\)	\(5.00\)	\(40.0\)

Análisis:

Sistema\(\rightarrow\) Ver la imagen

Periodo\(\rightarrow\) de tiempo Problema de tasa (Diferencia horaria infinitesimal)

Cosas para contar Especies\(\rightarrow\) químicas y masa.

Hay 6 incógnitas en este problema: un caudal másico y cinco composiciones. Por lo tanto, necesitamos 6 ecuaciones independientes para relacionar estas variables antes de poder resolver el problema.

Aplicar contabilidad de conservación de masas y especies. Dado que hay 3 compuestos podemos obtener como máximo 3 ecuaciones independientes escribiendo la contabilidad de especies y la conservación de ecuaciones de masa para el sistema. Escribamos ecuaciones para la masa total, etanol y metanol:

\[ \begin{align*} \text{Mass Balance:} \quad \cancel{ \frac{d m_{sys}}{dt} }^{=0, SS} &= \dot{m}_1 + \dot{m}_2 - \dot{m}_3 \\ 0 &= \dot{m}_1 + \dot{m}_2 - \dot{m}_3 \end{align*} \nonumber \]

\[\begin{align*} \text{Ethanol Balance:} \quad \frac{d m_{\text{eth, sys}}}{d t} &= \dot{m}_{\text{eth, 1}} + \dot{m}_{\text {eth, 2}} - \dot{m}_{\text {eth, 3}} = m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3} \\ 0 &= m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3} \end{align*} \nonumber \]

\[\begin{align*} \text{Methanol Balance:} \quad \frac{d m_{\text {meth, sys}}}{d t} &= \dot{m}_{\text {meth, 1}} + \dot{m}_{\text {meth, 2}} -\dot{m}_{\text {meth, 3}} = m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3} \\ 0 &= m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3} \end{align*} \nonumber \]

Dado que hemos utilizado todas las ecuaciones independientes de contabilidad de especies o balance de masas, ahora debemos pasar a las relaciones de composición. Hay tres entradas/salidas, por lo que a lo sumo podemos escribir 3 ecuaciones de composición, una para cada flujo de flujo:

\[ \begin{align*} \text{Stream 1:} & \quad 1=m f_{\text{meth, 1}} + m f_{\text{eth, 1}} + m f_{\text{w, 1}} \\ \text{Stream 2:} &\quad 1=mf_{\text{meth, 2}} + m f_{\text{eth, 2}} + m f_{\text{w, 2}} \\ \text{Stream 3:} &\quad 1=m f_{\text{meth, 3}} + m f_{\text{eth, 3}} + m f_{\text{w, 3}} \end{align*} \nonumber \]

Dado que el problema está en estado estacionario, no hay necesidad de una ecuación de composición que describa los contenidos del sistema.

Ahora tenemos seis ecuaciones que involucran a las seis incógnitas. Suponiendo que las ecuaciones son independientes, deberíamos poder resolverlas para las incógnitas. Si sustituimos la información conocida en las seis ecuaciones, tenemos lo siguiente:

\(0 = \dot{m}_1 + \dot{m}_2 - \dot{m}_3\)	\(\rightarrow\)	\(0 = \dot{m}_1 + \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right)\)
\(0 = m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3}\)	\(\rightarrow\)	\(0 = (0) \dot{m}_1 + m f_{\text{eth, 2}} \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - (0.40) \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right)\)
\(0 = m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3}\)	\(\rightarrow\)	\( 0 = m f_{\text{meth, 1}} + (0) \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - (0.05) \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) \)
\(1 = m f_{\text{meth, 1}} + m f_{\text{eth, 1}} + m f_{\text{w, 1}}\)	\(\rightarrow\)	\( 1 = m f_{\text{meth, 1}} + 0 + m f_{\text{w, 1}} \)
\(1 = m f_{\text{meth, 2}} + m f_{\text{eth, 2}} + m f_{\text{w, 2}}\)	\(\rightarrow\)	\( 1 = 0 + m f_{\text{eth, 2}} + m f_{\text{w, 2}} \)
\(1 = m f_{\text{meth, 3}} + m f_{\text{eth, 3}} + m f_{\text{w, 3}}\)	\(\rightarrow\)	\( 1 = 0.05 + 0.40 + m f_{\text{w, 3}} \)

Resolver estas ecuaciones da las siguientes respuestas:

Stream	Caudal másico	Composición — Masa%
		Metanol	Etanol	Agua
1	\( \mathbf{ 80 \ \mathrm{ \bf{kg}} / \mathrm{ \bf{h}} } \)	\(\bf{12.5}\)	\(0\)	\(\bf{87.5}\)
2	\( 120 \ \mathrm{kg} / \mathrm{h} \)	\(0\)	\(\bf{66.7}\)	\(\bf{33.3}\)
3	\(200 \ \mathrm{kg} / \mathrm{h} \)	\(5.00\)	\(40.0\)	\(\bf{55.0}\)

Esta solución se puede hacer a mano; sin embargo, es mejor hacerlo usando un sistema de álgebra computacional como MAPLE o un solucionador numérico como EES.

Lecciones a aprender de este problema:

En general, para cualquier problema con composición variable pero sin reacciones químicas,

• cada corriente de flujo se especifica conociendo su caudal másico (o molar) y las fracciones másicas (o molares) de los componentes en la corriente.
• los contenidos de cada sistema se describen conociendo la masa (o moles) y la composición de los contenidos.
• para cada sistema (o subsistema), puede escribir una ecuación de composición para cada flujo de flujo y una ecuación de composición para el contenido del sistema. Todas estas ecuaciones son independientes.
• para cada sistema (o subsistema) en el problema, puede escribir tantas ecuaciones contables independientes de masa y/o especies como compuestos químicos (componentes) en el sistema (o subsistema).

Para este ejemplo, hay un sistema con tres corrientes de flujo y tres compuestos:

• Número máximo de variables para describir las composiciones, la masa y los caudales:

\[(3 \text { mass flow rates})+(3 \text { flow streams})\left(3 \ \frac{\text {compounds}}{\text {flow stream}}\right)=12 \text { variables } \nonumber \]

• Número máximo de ecuaciones independientes que se pueden escribir usando composición, conservación masiva y contabilidad de especies:

\[\underbrace{(1 \text { system})(3 \text { compounds})}_{\begin{array}{c} \text { Number of independent total mass} \\ \text {and/or species accounting equations} \end{array}} + \underbrace{(3 \text { flow streams})}_{\begin{array}{c} \text {Number of independent} \\ \text {composition equations} \end{array}}=6 \text { independent equations} \nonumber \]

• El número de grados de libertad es la diferencia entre el número de variables necesarias para describir el problema y el número de ecuaciones independientes que puedes escribir:

\[\underbrace{ \text{DOF}} _ {\begin{array}{c} \text {Degrees of} \\ \text {Freedom} \end{array}} = \underbrace{\text { NOV }}_{\begin{array}{c} \text {Number of} \\ \text {Variables} \end{array}} - \underbrace{\text {NOE}}_{\begin{array}{c} \text {Number of} \\ \text{Independent} \\ \text {Equations} \end{array}}= 12 - 6 = 6= \left[\begin{array}{c} \text {Minimum number of variables} \\ \text {that must be specified to obtain} \\ \text {a unique solution.} \end{array}\right] \nonumber \]

• Para este ejemplo, la sentencia problem proporciona información sobre seis variables. Sin esta información hubiera sido imposible encontrar una solución única.
  Si sólo se hubieran asignado valores a cinco variables, sólo habría sido posible resolver para 6 de las variables restantes en términos de la séptima variable. Por ejemplo, si no se hubiera especificado el caudal másico a 2, podría haberlo tratado como una variable independiente y resuelto para todas las demás variables desconocidas en función de\(\dot{m}_{2}\). Para una solución físicamente posible, solo\(\dot{m}_{2}\) podría tomar un rango limitado de valores, por ejemplo,\(0<\dot{m}_{2}<200 \mathrm{~kg} / \mathrm{h}\) porque la corriente 2 es la única forma en que el etanol se lleva al mezclador.
  Con solo cinco variables especificadas, una solución única solo existiría si se proporcionan restricciones adicionales sobre el problema. Estos podrían proporcionarse de varias maneras, especificando cómo algunos de los flujos de masa o especies entrantes deben distribuirse en la salida, brindándole una gama de composiciones para ciertas variables, etc. Estas restricciones sirven como ecuaciones independientes que se pueden combinar con las ecuaciones independientes desarrollado a partir de la composición y la contabilidad de especies/masas. Este conjunto puede entonces ser resuelto para las variables desconocidas.
  Si se asignaran valores a más de seis variables, no todas podrían tomar valores arbitrarios para que el problema tuviera una solución.

Ejemplo — Enriquecimiento de una mezcla de gases

Un cilindro de gas inicialmente contiene\(10 \ \mathrm{lbm}\) aire. Se desea enriquecer el contenido de oxígeno de la mezcla mediante la purga\(5 \ \mathrm{lbm}\) de aire del cilindro y luego la adición\(3 \ \mathrm{lbm}\) de\(\mathrm{O}_{2}\). Determinar la masa y composición molar de la mezcla una vez finalizado el proceso de enriquecimiento. Para fines de análisis se puede suponer que el aire es una mezcla de\(23 \%\) oxígeno y\(77 \%\) nitrógeno en masa.

Solución

Conocido: El aire se desangra de un cilindro de gas y se reemplaza por oxígeno.

Buscar: Composición (fracciones de masa y moles) después del proceso

Dado:

Figura\(\PageIndex{3}\): The system inside the tank.

\[ \begin{align*} \text{State 1:} \quad &m_{1}=10 \ \mathrm{lbm} \\ &m f_{\mathrm{O}_2}=0.23 ; \quad m f_{\mathrm{N}_2}=0.77 \end{align*} \nonumber \]

\[ \begin{align*} \text{Process 1} \rightarrow 2: \quad& \text{Remove } 5 \ \mathrm{lbm} \text{ air} \\ &\text{Add } 3 \ \mathrm{lbm} \text{ oxygen} \end{align*} \nonumber \]

Análisis:

Estrategia\(\rightarrow\) Para encontrar composiciones debemos conocer la masa total y la masa de cada componente en el tanque al final del proceso de enriquecimiento. Si podemos encontrar la masa total y la masa de cada componente en el estado final, podemos responder a esta pregunta. Así, supongamos que tenemos tres incógnitas. Para resolverlos aplicaremos una ecuación contable ya que queremos relacionar los contenidos de un sistema en dos momentos diferentes.

Sistema\(\rightarrow\) Trate el interior del tanque como un sistema abierto no deformante.

\(\rightarrow\)Masa de propiedad y especies químicas

Período de tiempo\(\rightarrow\) Dado que solo el interés en los estados inicial y final probablemente requiera forma de tiempo finito

Escribir la conservación de la masa para cualquier momento durante el proceso de enriquecimiento y luego integrarlo en el intervalo de tiempo del enriquecimiento da:

\[\frac{d m_{sys}}{d t} = \dot{m}_{in} - \dot{m}_{out} \quad \rightarrow \quad \int\limits_{t_1}^{t_2} \left( \frac{d m_{sys}}{d t} \right) dt = \int_{t_1}^{t_2} \left( \dot{m}_{in} - \dot{m}_{out} \right) dt \quad \rightarrow \quad m_{sys, 2}-m_{sys, 1} = m_{in}-m_{out } \nonumber \]

También se puede escribir una expresión similar para cada especie química en el problema:\[\begin{align*} \text{O}_{2}: \quad & \frac{d m_{sys, \text{O}_2}}{d t} = \dot{m}_{in, \ \text{O}_2} - \dot{m}_{out, \ \text{O}_2} & \rightarrow & m_{sys, \ \text{O}_2, \ 2} - m_{sys, \ \text{O}_2, \ 1} = m_{in, \ \text{O}_2} - m_{out, \ \text{O}_2} \\[4pt] \text{N}_{2}: \quad & \frac{d m_{sys, \ \text{N}_2}}{d t} = \dot{m}_{in, \ \text{N}_2} - \dot{m}_{out, \ \text{N}_2} & \rightarrow & m_{sys, \ \text{N}_2, \ 2} - m_{sys, \ \text{N}_2, \ 1} = m_{in, \ \text{N}_2} - m_{out, \ \text{N}_2} \end{align*} \nonumber \]

Esto da tres ecuaciones; sin embargo, sólo dos de ellas son independientes, es decir, la tercera ecuación puede estar formada por una combinación lineal de las otras dos ecuaciones.

Para obtener la tercera ecuación independiente, considere la composición en el Estado 2. Esto se puede escribir en una de dos formas:
\(\quad\) En cuanto a la masa real que tenemos\( \quad m_{sys, 2} = m_{sys, \text{O}_2, 2} + m_{sys, \text{N}_2, 2}\)
\(\quad\) En cuanto a las fracciones de masa tenemos\(\quad 1=m f_{sys, \text{O}_2, 2} + m f_{sys, \text{N}_2, 2}\)

Como puede ver fácilmente, estas dos ecuaciones no son independientes ya que la segunda ecuación es solo la primera ecuación dividida por la masa del sistema.

Resolviendo para la misa final\[m_{sys, \ 2}=m_{sys, \ 1} + m_{in} - m_{out} = (10+3-5) \ \mathrm{lbm} = 8 \ \mathrm{lbm} \nonumber \]

Ahora para encontrar la cantidad de oxígeno y nitrógeno en el estado final

m_ {sys,\\ texto {N} _2,\ 2} - m_ {sys,\\ texto {N} _2,\ 1} =\ cancel {m_ {in,\\ text {N} _2}} ^ {=0} - m_ {out,\\ text {N} _2}

m_ {out,\\ text {N} _2} = m f_ {out,\\ text {N} _2}\ cdot m_ {out} = (0.77) (5\\ text {lbm}) = 3.85\\ texto {lbm}\ quad\ fila derecha\ quad m_ {sys,\\ texto {N} _2,\ 2} = (7.70 - 3.85)\\ texto {lbm} = 3.85\\ texto {lbm}

m_ {sys,\\ texto {N} _2,\ 1} = m f_ {sys,\\ texto {N} _2,\ 1}\ cdot m_ {sys,\ 1} = (0.77) (10\\ texto {lbm}) = 7.70\\ texto {lbm}

m_ {sys,\ 2} = m_ {sys,\\ texto {N} _2,\ 2} + m_ {sys,\\ texto {O} _2,\ 2}\ cuádruple\ fila derecha\ cuádruple

Ahora para encontrar las composiciones, use una tabla simple como se muestra a continuación:

	\(\frac{m_{j}}{\mathrm{lbm}}\)	\(m f_{j}\)	\(\frac{M_{j}}{(\mathrm{lbm} / \mathrm{lbmol})}\)	\(\frac{n_{j}}{\mathrm{lbmol}}\)	\(n f_{j}\)
\(\mathrm{O}_{2}\)	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(4.15\)	\ (m f_ {j}\) ">\(0.519\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(32.00\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.1297\)	\ (n f_ {j}\) ">\(0.485\)
\(\mathrm{N}_{2}\)	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(3.85\)	\ (m f_ {j}\) ">\(0.481\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(28.01\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.1375\)	\ (n f_ {j}\) ">\(0.515\)
	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(8.00\)	\ (m f_ {j}\) ">\(1.000\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(\ldots \ldots\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.2672\)	\ (n f_ {j}\) ">\(1.000\)

El porcentaje en peso de oxígeno ha aumentado desde\(23 \%\) inicialmente hasta un valor final de\(51.9 \%\).

Comentario:

Tenga en cuenta que las fracciones de masa\((m f)\) y las fracciones molares no\((n f)\) son las mismas. Como se indica a continuación la fracción de masa indica la composición en términos de la cantidad de masa de cada componente mientras que la fracción molar sólo considera el número de moléculas de las partículas. \

[\ begin {alinear*} m f &\ fila derecha\ frac {\ texto {masa de} j\ texto {moléculas}} {\ texto {masa total de moléculas}}\\ n f &\ fila derecha\ frac {\ texto {número de} j\ texto {moléculas}} {\ texto {número total de moléculas}}\ end {alinear*}\ nonumber\]

Ejemplo — Proceso continuo de destilación rápida

Una corriente de alimentación líquida se alimenta continuamente a una cámara de destilación rápida. A medida que el líquido ingresa a la cámara, su presión se reduce y parte del líquido entrante destella a vapor. La corriente de fondo líquido se drena del piso de la cámara y el destilado de vapor se retira cerca de la parte superior de la cámara.

La corriente de alimentación consiste en agua, etanol, metanol entrando a los 25\(\mathrm{lbm} / \mathrm{h}\)\(10 \mathrm{lbm} / \mathrm{h}\), y\(5 \mathrm{lbm} / \mathrm{h}\), respectivamente. La corriente de fondo tiene un caudal másico de\(24 \mathrm{lbm} / \mathrm{h}\) y consiste en\(83.3 \%\) agua,\(12.5 \%\) etanol y\(4.2 \%\) metanol en peso.

Determinar la composición (fracciones de masa y moles) y el caudal másico del destilado.

Solución

Conocido: Condiciones de funcionamiento para una cámara de destilación flash continua.

Encuentra: Composición (fracciones de masa y moles) y caudal másico del destilado.

Dado:

Figura\(\PageIndex{4}\): El sistema dentro de la cámara de flash.

arroyos
\(1- \text{Feed}\)	\(\dot{m}_{\text {Water}}=25 \mathrm{lbm} / \mathrm{h}\) \(\dot{m}_{\text {Ethanol}}=10 \mathrm{lbm} / \mathrm{h}\) \(\dot{m}_{\text {Methanol}}=5 \mathrm{lbm} / \mathrm{h}\)
\(2- \text{Distillate}\)
\(3- \text{Bottoms}\)	\(m f_{\text {Water}}=83.3 \%\) \(m f_{\text {Ethanol}}=12.5 \%\) \(m f_{\text {Methanol}}=4.2 \%\) \(\dot{m}=24 \mathrm{lbm} / \mathrm{h}\)

Análisis:

Estrategia\(\rightarrow\) Dado que nos interesa relacionar los flujos de entrada con los flujos de salida, esto parece un candidato para la conservación de la contabilidad de masas y especies.

Sistema\(\rightarrow\) No deformante, sistema abierto formado por el volumen del interior del tanque

Propiedad\(\rightarrow\) Masa y especies ya que tenemos mezclas que cambian de composición

Período de tiempo\(\rightarrow\) Dado que el sistema se alimenta continuamente, asuma el estado estacionario

Para especificar completamente todas las entradas y salidas de un problema como este requiere conocer la composición y el caudal másico total en cada entrada/salida O el caudal másico para cada especie y el caudal másico total en cada entrada/salida. Así, el número total de incógnitas es

\[ \underbrace{ \left[ \left( \text{Number of Species} \right) + 1 \right] }_{mf_{j} \text{'s and } \dot{m}} \times \left[ \text{Number of inlets/outlets} \right] = \left[ 3 \times 1 \right] \times \left[ 3 \right] = \underbrace{ 12 \ \text{unknowns} }_{\begin{array}{c} mf_{\text{Water}}, \ mf_{\text{Ethanol}}, \ mf_{\text{Methanol}}, \ \dot{m} \\ \text {for feed, distillate, and bottoms} \end{array}} \nonumber \]

\[ \underbrace{ \left[ \left( \text{Number of Species} \right) + 1 \right] }_{mf_{j} \text{'s and } \dot{m}} \times \left[ \text{Number of inlets/outlets} \right] = \left[ 3 \times 1 \right] \times \left[ 3 \right] = \underbrace{12 \text{ unknowns} }_ {\begin{array}{c} \dot{m}_{\text{Water}}, \ \dot{m}_{\text{Ethanol}}, \ \dot{m}_{\text{Methanol}} \\ \text {for feed, distillate, and bottoms} \end{array}} \nonumber \]

Para ayudar a visualizar lo que sabemos y lo que no sabemos, configura una tabla:

	\(\dot{m}_{j} \ (\mathrm{lbm} / \mathrm{h}) \)	Composición
	\ (\ punto {m} _ {j}\ (\ mathrm {lbm}/\ mathrm {h})\) ">	\(\text{Water}\)	\(\text{Ethanol}\)	\(\text{Methanol}\)
\(1 - \text{Feed}\)	\ (\ punto {m} _ {j}\ (\ mathrm {lbm}/\ mathrm {h})\) ">\(\text{Eq. } 1\)	\(\text{Eq. } 2\)	\(\text{Eq. } 3\)	\(\text{Eq. } 4\)
\(2 - \text{Distillate}\)	\ (\ punto {m} _ {j}\ (\ mathrm {lbm}/\ mathrm {h})\) ">\(\text{Eq. } 5\)	\(\text{Eq. } 6\)	\(\text{Eq. } 7\)	\(\text{Eq. } 8\)
\(3 - \text{Bottoms}\)	\ (\ punto {m} _ {j}\ (\ mathrm {lbm}/\ mathrm {h})\) ">\(24.0\)	\(83.3\)	\(12.5\)	\(4.2\)

Al observar la tabla vemos que ya tenemos cuatro piezas de información. Dados los caudales másicos en la corriente de alimentación, podemos encontrar la composición en la corriente de alimentación usando una relación de composición de corriente de alimentación\((\text{Eq. }1)\)

\[ \text{Eq. }1 \quad \rightarrow \quad \dot{m}_1 = \dot{m}_{\text {Water}, \ 1} + \dot{m}_{\text {Ethanol}, \ 1} + \dot{m}_{\text {Methanol}, \ 2} = (25+10+5) \ \frac{\mathrm{lbm}}{\mathrm{h}} = 40 \ \frac{\mathrm{lbm}}{\mathrm{h}} \nonumber \]

Luego usando la definición de fracciones de masa\((\text{Eq. } 2, \ 3,\) y\(4)\) para la corriente de alimentación:

\[ \text{Eq. } 2, \ 3, \ 4 \quad \rightarrow \quad m f_{\text {Water}, \ 1} = \frac{\dot{m}_{\text {water}, \ 1}}{\dot{m}_1} = \frac{25}{40} = 62.5 \% \ ; \quad m f_{\text {Ethanol}, \ 1} = \frac{10}{40}=25.0 \% \ ; \quad m f_{\text {Methanol}, \ 1} = \frac{5}{40}=12.5 \% \nonumber \]

Ahora sólo quedan cuatro incógnitas. El caudal másico total se puede resolver para escribir la conservación de la masa para el sistema\((\text{Eq. } 5)\)

\[ \text{Eq. } 5 \rightarrow \underbrace{ \cancel{ \frac{d m_{sys}}{dt} }^{=0} }_{\begin{array}{c} \text{steady-state} \\ \text{conditions} \end{array}} = \dot{m}_1 - \dot{m}_2 - \dot{m}_3 \quad \rightarrow \quad \dot{m}_2 = \dot{m}_1 - \dot{m}_3 = (40 - 24) \ \frac{\mathrm{lbm}}{\mathrm{h}} = 16 \ \frac{\mathrm{lbm}}{\mathrm{h}} \nonumber \]

Las incógnitas restantes se pueden determinar aplicando la ecuación contable de especies para agua, etanol y metanol. Las ecuaciones resultantes se ven igual\(\text{Eq. } 5\), excepto que están escritas para cada especie.

\[ \begin{align*} &\dot{m}_{\text {water}, \ 2} = \dot{m}_{\text {water}, \ 1} - \dot{m}_{\text {water}, \ 3} = \dot{m}_{\text {water}, \ 1} - m f_{\text {water}, \ 3} \dot{m}_3 = [25.0 - (0.833)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 5.01 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {water}, \ 2} = \frac{\dot{m}_{\text {water}, \ 2}}{\dot{m}_2} = \frac{5.01}{16.0} = 31.3 \% \end{align*} \nonumber \]

\[ \begin{align*} &\dot{m}_{\text {ethanol}, \ 2} = \dot{m}_{\text {ethanol}, \ 1} - \dot{m}_{\text {ethanol}, \ 3} = \dot{m}_{\text {ethanol}, \ 1} - m f_{\text {ethanol}, \ 3} \dot{m}_3 = [10.0-(0.125)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 7.00 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {ethanol}, \ 2} = \frac{\dot{m}_{\text {ethanol}, \ 2}}{\dot{m}_2} = \frac{7.00}{16.0}=43.7 \% \end{align*} \nonumber \]

\[ \begin{align*} &\dot{m}_{\text {methanol}, \ 2} = \dot{m}_{\text {methanol}, \ 1} - \dot{m}_{\text {methanol}, \ 3} = \dot{m}_{\text {methanol}, \ 1} - m f_{\text {methanol}, \ 3} \dot{m}_{3} = [5.0-(0.042)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 3.99 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {methanol}, \ 2} = \frac{\dot{m}_{\text {methanol}, \ 2}}{\dot{m}_2} = \frac{3.99}{16.0} = 25.0 \% \end{align*} \nonumber \]

La composición molar del destilado se puede calcular después de encontrar los caudales molares:

	Caudal másico	Masa molar	Caudal molar	Fracción molar
\(\text{Water}\)	\(5.01 \ \mathrm{lbm} / \mathrm{h}\)	\(18.02 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.2780 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.409\)
\(\text{Ethanol}\)	\(7.00 \ \mathrm{lbm} / \mathrm{h}\)	\(46.07 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.1519 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.224\)
\(\text{Methanol}\)	\(3.99 \ \mathrm{lbm} / \mathrm{h}\)	\(32.05 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.2494 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.367\)
	\(16.00 \ \mathrm{lbm} / \mathrm{h}\)	\(\cdots\)	\(0.6793 \ \mathrm{lbmol} / \mathrm{h}\)	\(1.000\)

Sistemas con reacciones químicas

Cuando ocurren reacciones químicas en un sistema, los términos de consumo y generación ya no son cada cero. Para evaluar estas expresiones, se debe confiar en las ecuaciones químicas equilibradas apropiadas que se apliquen a las reacciones involucradas. Debido a esto, la forma molar de la ecuación contable de especies es la que se usa comúnmente cuando ocurren reacciones químicas.

Nuevamente, es importante reconocer exactamente cuántas ecuaciones independientes se pueden obtener aplicando la contabilidad de conservación de masas y especies.

Para un sistema reactivo, el número de ecuaciones independientes que se pueden obtener de la conservación de la masa y la contabilidad de especies es igual al número de especies independientes más el número de reacciones químicas independientes. (Las ecuaciones adicionales son suministradas por las ecuaciones químicas balanceadas para cada reacción independiente).

Las aplicaciones para sistemas con reacciones químicas están fuera del alcance de este texto. Sin embargo, un breve ejemplo ilustrará cómo se obtienen términos de generación y consumo a partir de las ecuaciones químicas. Estos temas se manejan con mayor detalle en los cursos de ingeniería química. El último ejemplo de esta sección demuestra cómo se podría abordar un problema con las reacciones químicas.

Ejemplo —Making\(\mathrm{CO}_2\)

Un tanque contiene\(2 \ \mathrm{kmol}\) de monóxido de carbono\((\mathrm{CO})\) y\(2 \ \mathrm{kmol}\) de oxígeno\(\left(\mathrm{O}_{2}\right)\). Si\(50 \%\) de la cantidad original de\(\mathrm{CO}\) se hace reaccionar con el\(\mathrm{O}_{2}\) para formar\(\mathrm{CO}_{2}\), determinar la cantidad de\(\mathrm{CO}, \mathrm{CO}_{2}\), y\(\mathrm{O}_{2}\) en la mezcla final.

Solución

Conocido: Una mezcla de\(\mathrm{CO}\) y\(\mathrm{O}_{2}\) se hace reaccionar en un sistema cerrado.

Encuentra: Cantidad de\(\mathrm{CO}, \mathrm{O}_{2}\), y\(\mathrm{CO}_{2}\) en mezcla si\(50 \%\) de original\(\mathrm{CO}\) se hace reaccionar.

Dado:

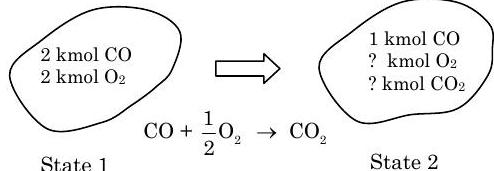
Figura\(\PageIndex{5}\): Estados 1 y 2 del sistema, y la reacción química responsable del cambio en los estados.

Análisis:

Estrategia\(\rightarrow\) Dado que esto implica mezclas de sustancias y reacciones, utilice la contabilidad de especies.

Sistema\(\rightarrow\) Considere un sistema cerrado que incluya toda la masa inicialmente en el sistema.

Propiedad para contar Especies\(\rightarrow\) químicas

Periodo de tiempo\(\rightarrow\) Desde interesado en estado de inicio y finalización, utilice la forma de tiempo finito.

En general para cada especie\(j\)

\[\frac{d n_{sys, j}}{d t} = \underbrace{ \cancel{ \sum_{in} \dot{n}_{j, i} - \sum_{out} n_{j, e} }^{=0} }_{\text {closed system}}+\dot{n}_{j, \ gen} - \dot{n}_{j, \ cons} \quad \rightarrow \quad \underbrace{ n_{j, 2} - n_{j, 1} }_{\begin{array}{c} \text{dropped the system} \\ \text{subscript} \end{array}} = n_{j, \ gen} - n_{j, \ cons} \nonumber \]

Ahora para cada especie

\[ \begin{align*} & \text{CO:} \quad &\cancel{ n_{\text{CO}, \ 2} }^{=0} + \cancel{ n_{\text{CO}, \ 1} }^{=0} = \cancel{ n_{\text{CO}, \ gen} }^{=0} - n_{\text{CO}, \ cons} \quad &\rightarrow \quad\quad n_{\text{CO}, \ cons} = 1 \ \text{kmol} \\ & \text{O}_2: \quad &n_{\text{O}_2, \ 2} - \cancel{ n_{\text{O}_2, \ 1} }^{=0} = \cancel{ n_{\text{O}_2, \ gen} }^{=0} - n_{\text{O}_2, \ cons} \quad &\rightarrow \quad\quad n_{\text{O}_2, \ 2} = -n_{\text{O}_2, \ cons} \\ &\text{CO}_2: \quad &n_{\text{CO}_2, \ 2} - \cancel{ n_{\text{CO}_2, \ 1} }^{=0} = n_{\text{CO}_2, \ gen} - \cancel{ n_{\text{CO}_2, \ cons} }^{=0} \quad &\rightarrow \quad\quad n_{\text{CO}_2, \ 2} = n_{\text{CO}_2, \ gen} \end{align*} \nonumber \]

Esto nos da cuatro incógnitas y sólo dos ecuaciones. Para obtener las ecuaciones restantes, mire la ecuación de reacción química. En términos de consumo y generación, la reacción química es la siguiente:

\[\begin{gathered} n_{\text {CO}, \ cons} \mathrm{CO} + n_{\text{O}_2, \ cons} \mathrm{O}_2 \rightarrow n_{\text{CO}_2, \ gen} \mathrm{CO}_2 \\[4pt] \mathrm{CO} + \frac{n_{\text{O}_2, \ cons}}{n_{\text {CO}, \ cons}} \mathrm{O}_2 \rightarrow \frac{n_{\text{CO}_2, \ gen }}{n_{\text {CO}, \ cons }} \mathrm{CO}_2 \end{gathered} \nonumber \]

Si comparamos esta ecuación con la ecuación química equilibrada para la reacción de\(\mathrm{CO}\) con\(\mathrm{O}_2\) para formar\(\mathrm{CO}_2\), podemos determinar las dos ecuaciones restantes entre las incógnitas:

\[\begin{array}{c} \mathrm{CO} + \dfrac{n_{\text{O}_2, cons}}{n_{\text{CO}, \ cons}} \mathrm{O}_2 \rightarrow \dfrac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} \mathrm{CO}_{2} \\[4pt] \mathrm{CO} + \frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{CO}_2 \end{array} \quad \Rightarrow \quad \frac{n_{\text{O}_2, \ cons}}{n_{\text{CO}, \ cons}} = \frac{1}{2} \quad \& \quad \frac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} = 1 \nonumber \]

Así, las composiciones finales son las siguientes:\[\begin{align*} &n_{\text{CO}, \ 2} = 1 \ \mathrm{kmol} \\ &n_{\text{O}_2, \ 2} = n_{\text{O}_2, \ gen} = \frac{n_{\text{O}_2, \ gen}}{n_{\text{CO}, \ cons}} n_{\text{CO}, \ cons} = \left( \frac{1}{2} \right) (1 \ \mathrm{kmol}) = \frac{1}{2} \ \mathrm{kmol} \\[4pt] &n_{C\text{O}_2, \ 2} = n_{\text{CO}_2, \ gen} = \frac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} n_{\text{CO}, cons}=(1)(1 \ \mathrm{kmol}) = 1 \ \mathrm{kmol} \end{align*} \nonumber \]

Comentarios:

(1) La mezcla final se ha\(3.5 \ \mathrm{kmol}\) comparado con\(4.0 \ \mathrm{kmol}\) la mezcla inicial. Por lo general, los moles no se conservan.

(2) Un enfoque alternativo es escribir ecuaciones contables de especies para las especies atómicas,\(\text{C}\) y\(\text{O}\). Tenga en cuenta que las especies atómicas, al igual que la masa total, se conservan.