7.3: Conservación de la Energía

El punto de partida recomendado para cualquier aplicación de la conservación de energía es la forma de tasa de la ecuación de conservación de energía:

\[\frac{dE_{\text {sys}}}{dt} = \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} + \left[\sum_{\text {in}} \dot{m}_{i}\left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text {out}} \dot{m}_{e}\left(h_{e}+\frac{V_{e}^{2}}{2}+g z_{e}\right)\right] \nonumber \]

Recuerde, la única restricción incorporada en esta ecuación es que la masa que cruza el límite del sistema solo puede llevar consigo energía interna, energía cinética traslacional y energía potencial gravitacional. Si se requiere una forma más general, solo necesitamos agregar "\(+e_{\text {other}}\)" después del término específico de energía potencial gravitacional,\(g z\).

Al aplicar esta ecuación para describir el comportamiento de un sistema, existen varios supuestos de modelado que se utilizan comúnmente. Estos se describen con detalle en los siguientes párrafos. Como siempre, debes enfocarte en comprender la física que subyace a la suposición y cómo se usan. No se limite a memorizar las ecuaciones simplificadas.

Sistema de estado estacionario

Si un sistema está operando en condiciones de estado estacionario, todas las propiedades e interacciones intensivas son independientes del tiempo. Así, la energía del sistema es una constante,\(E_{\text {sys}}= \text{constant}\). Cuando se aplica a la ecuación de conservación de energía se tiene

\[\begin{aligned} \underbrace{\cancelto{0}{ \frac{d E_{\text{sys}}}{dt} }}_{E_{\text{sys}} = \text{constant}} &= \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} + \left[\sum_{\text {in}} \dot{m}_{i} \left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(h_{e}+\frac{V_{e}^{2}}{2}+g z_{e}\right)\right] \\ 0 &= \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} + \left[\sum_{\text{in}} \dot{m}_{i} \left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(h_{e}+\frac{V_{e}^{2}}{2}+g z_{e}\right)\right] \end{aligned} \nonumber \]En palabras, la suma de las tasas netas de transporte de energía por trabajo, transferencia de calor y masa debe ser igual a cero.

Sistema cerrado

Un sistema cerrado no tiene flujo másico a través de su límite. Con esta restricción, la ecuación de conservación de energía se simplifica de la siguiente manera:\[\begin{aligned} &\frac{d E_{\text {sys}}}{dt} = \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} + \underbrace{ \cancelto{0}{ \left[\sum_{\text{in}} \dot{m}_{i} \left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(h_{e}+\frac{V_{e}^{2}}{2}+g z_{e}\right)\right] }}_{\text {No mass flow rates }} \\[4pt] &\frac{d E_{\text {sys}}}{dt} = \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} \end{aligned} \nonumber \]

Tiempo finito, sistema cerrado

Para un sistema cerrado en un intervalo de tiempo finito, primero aplique la suposición del sistema cerrado y luego integre la ecuación durante el intervalo de tiempo especificado:

\[\begin{gathered} \frac{d E_{\text {sys}}}{dt} = \dot{W}_{\text{net, in}} + \dot{Q}_{\text{net, in}} + \cancel{ \left[\sum_{\text{in}} \dot{m}_{i} \left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text{out}} \dot{m}_{e} \left(h_{e}+\frac{V_{e}^{2}}{2}+gz_{e}\right)\right] }^{=0} \\[4pt] \frac{d E_{\text{sys}}}{dt} = \dot{W}_{\text{net, in}} + \dot{Q}_{\text{net, in}} \\ \int\limits_{t_1}^{t_2} \left(\frac{d E_{\text{sys}}}{dt}\right) dt = \int\limits_{t_1}^{t_2} \left(\dot{W}_{\text{net, in}} + \dot{Q}_{\text{net, in}}\right) dt \\ \int\limits_{1}^{2} d E_{\text{sys}} = \int\limits_{1}^{2} \left(\delta W_{\text{net, in}}+\delta Q_{\text{net, in}}\right) \quad \rightarrow \quad \Delta E_{\text{sys}} = W_{\text{net, in}}+Q_{\text{net, in}} \end{gathered} \nonumber \]

En palabras, esto dice que el cambio en la energía del sistema equivale al transporte neto de energía al sistema por trabajo y por transferencia de calor.

Supuestos sobre transferencia de calor y trabajo:

Uno de los aspectos de aplicar la conservación de energía que frecuentemente desconcierta a los estudiantes es la necesidad de decir algo sobre la transferencia de calor y las interacciones de trabajo para el sistema que estamos modelando.

Transferencia de calor:

En este curso, solemos hacer uno de tres supuestos sobre la transferencia de calor de energía para un sistema:

1. No hay transferencia de calor. Esto se llama proceso adiabático o sistema adiabático. Físicamente, aplicar aislamiento térmico a la superficie se aproxima a una superficie adiabática. Desafortunadamente, no existen aislantes térmicos perfectos; sin embargo, si la escala de tiempo del proceso es pequeña en relación con el tiempo que tarda en ocurrir la transferencia de calor de energía, entonces la suposición adiabática suele ser buena.
2. La tasa de transferencia de calor\(Q\) o transferencia de calor\(\dot{Q}\) es lo desconocido que estamos resolviendo en el problema.
3. La tasa de transferencia de calor\(Q\) o transferencia de calor\(\dot{Q}\) se da en la declaración del problema.

Recuerde que la transferencia de calor solo se puede definir con respecto a un límite. Si mueve el límite, cambia la transferencia de calor. Sin indicar claramente el límite de su sistema, es imposible aplicar ninguno de estos supuestos.

El estudio de la transferencia de calor como disciplina intenta relacionar la tasa de transferencia de calor en un límite con otras características del sistema, como la conductividad térmica, el coeficiente de transferencia de calor por convección y la diferencia de temperatura a través del límite. En algunos problemas, se le puede dar una relación constitutiva específica que le permita calcular la tasa de transferencia de calor sin utilizar la conservación de energía, similar a nuestras ecuaciones de trabajo. En todos los demás casos, supongamos que la transferencia de calor se puede modelar utilizando uno de los tres supuestos enumerados anteriormente.

Trabajo:

En este curso centraremos la mayor parte de nuestra atención en cuatro de los posibles mecanismos de trabajo. La clave para hacer la suposición correcta es examinar cuidadosamente el sistema que seleccione e identificar cualquier interacción que parezca funcionar. (Físicamente, imagina caminar por el sistema y buscar alguna pista que te lleve a creer que uno de estos mecanismos está presente). Recuerde que el trabajo solo se define con respecto a un límite. ¡Sin límites, sin trabajo! Aquí hay algunas pistas para cada uno de los cuatro mecanismos de trabajo:

1. Trabajo de compresión-expansión (PdV): vea si algún límite del sistema se mueve en una dirección normal a la superficie, por ejemplo, un límite al lado de un pistón.
2. Trabajo eléctrico: vea si el límite de su sistema corta algún cable eléctrico.
3. Trabajo del eje: busque si el límite del sistema corta algún eje giratorio.
4. Trabajo mecánico y potencia — mira para ver si hay alguna otra fuerza que se mueva en los límites del sistema.

Cuando revisemos el trabajo más tarde podemos identificar algunos mecanismos más; sin embargo, esta lista será suficiente para una amplia gama de problemas importantes.

Supuestos sobre la sustancia:: Otro problema nuevo y a veces desconcertante que encuentran los estudiantes al aplicar la ecuación de conservación de energía es la necesidad de evaluar las propiedades termofísicas —\(u\)\(h\)\(s\),\(T\),\(P\),,\(\rho\), y\(\upsilon\). Esto requiere un conocimiento empírico sobre el comportamiento del material dentro del sistema. Este conocimiento representa una ecuación constitutiva que nos permite predecir los valores de las propiedades una vez que hemos identificado el estado de la sustancia. Retrasaremos esta complicación por un tiempo, pero en breve introduciremos dos modelos de sustancias que describen con precisión el comportamiento de gases, líquidos y sólidos bajo ciertas condiciones.

Ejemplo — Arranque del motor

(adaptado de Moran & Shapiro, Termodinámica)

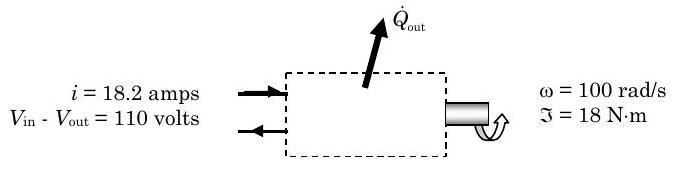
En condiciones de funcionamiento de estado estacionario, el eje de un motor gira a una velocidad constante de\(955 \mathrm{~rpm~} (100 \mathrm{~rad} / \mathrm{s})\) y aplica un par constante de\(18 \mathrm{~N} \cdot \mathrm{m}\) a una carga externa, y el motor de 110 voltios consume una corriente eléctrica constante de\(18.2\) amperios.

Figura\(\PageIndex{1}\): Un motor eléctrico gira un eje.

(a) Determinar la magnitud y dirección de la tasa de transferencia de calor en estado estacionario para el motor, en\(\mathrm{kW}\).

b) Durante el transitorio de arranque, la velocidad de transferencia de calor entre el motor eléctrico y su entorno varía con el tiempo de la siguiente manera:\[\dot{Q}_{\text {out}} = \dot{Q}_{\text {out, ss}} \left[1-e^{-t /(20 \mathrm{~s})}\right] \nonumber \] donde\(Q_{\text{out, ss}}\) está la tasa de transferencia de calor en estado estacionario del motor. Obtenga una expresión para la tasa de cambio de tiempo de la energía del motor usando su resultado de la Parte (a) y la ecuación de velocidad de transferencia de calor anterior.

Solución

Conocido: Un motor funciona con condiciones de funcionamiento conocidas

Encuentre: (a) Tasa de transferencia de calor en estado estacionario desde el motor, pulg\(\mathrm{kW}\).
(b) Tasa temporal de cambio de la energía del motor durante el transitorio de arranque.

Dado: Durante el arranque transitorio:\(\dot{Q}_{\text {out}} = \dot{Q}_{\text {out, ss}} \left[1-e^{-t /(20 \mathrm{~s})}\right]\)

Figura\(\PageIndex{2}\): Transferencias conocidas de calor y trabajo entre el sistema del motor y su entorno.

Análisis:

Estrategia\(\rightarrow\) Debido a que la pregunta involucra energía y transferencia de calor, intente la conservación de energía.
Sistema\(\rightarrow\) Tomar el motor como un sistema cerrado
Propiedad para contar\(\rightarrow\) Energía Período de
tiempo\(\rightarrow\) Ambas partes parecen requerir la forma de tasa (intervalo de tiempo infinitesimal)

Dibujando un sistema e identificando los transportes de energía, tenemos la figura a continuación.

Figura\(\PageIndex{3}\): Sistema con transportes de energía identificados de entrada y salida.

Ahora aplicando la forma de sistema cerrado de la forma de tasa de la ecuación de conservación de energía, tenemos:\[\frac{d E_{\text {sys}}}{dt} = \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} = \dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}}-\dot{Q}_{\text {out}} \nonumber \] donde hemos utilizado los subíndices para indicar las direcciones positivas correspondientes a nuestro diagrama

Para la parte (a) se nos pide considerar la tasa de transferencia de calor en estado estacionario, por lo tanto\[\underbrace{ \frac{dE_{\text{sys}}}{dt} }_{\text {Steady state}} = \dot{W}_{\text {electric, in}} - \dot{W}_{\text {shaft, out}} - \dot{Q}_{\text {out}} \quad \rightarrow \quad \dot{Q}_{\text {out}}=\dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}} \nonumber \]

Ahora tenemos que determinar la potencia eléctrica y la potencia del eje usando sus ecuaciones definitorias:\[\begin{aligned} \dot{W}_{\text {electric, in }} &= i \cdot \left(V_{\text{in}-\text{o}} - V_{\text{out}-\text{o}}\right) \quad\quad & \dot{W}_{\text{shaft, out}} &= \tau \cdot \omega \\ &=(18.2 \mathrm{~A}) \cdot (110 \mathrm{~V}) & &= (18.0 \mathrm{~N} \cdot \mathrm{m}) \cdot (100 \mathrm{~rad} / \mathrm{s}) \\ &= 2.00 \times 10^{3} \mathrm{~W} & &= 1.80 \times 10^{3} \mathrm{~W} \\ &=2.00 \mathrm{~kW} & &=1.80 \mathrm{~kW} \end{aligned} \nonumber \]

Sustituyendo estos resultados de nuevo en el balance energético de estado estacionario, tenemos\[\dot{Q}_{\text {out}}=\dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}} = (2.00-1.80) \mathrm{~kW}=0.20 \mathrm{~kW} \nonumber \]

Ahora por la parte (b), nos interesa la tasa de almacenamiento de energía en el motor, no la cantidad de energía almacenada en el motor. Comenzando con la forma de tasa del balance energético que tenemos\[\frac{d E_{\text{sys}}}{dt} = \dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}}-\dot{Q}_{\text {out}} = \dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}} - \dot{Q}_{\text {out, ss}} \left[1-e^{-t /(20 \mathrm{~s})}\right] \nonumber \] después de sustituir en la información dada la tasa de transferencia de calor.

Suponiendo que el eje y las potencias eléctricas son constantes durante este transitorio dará el siguiente resultado:\[\begin{aligned} \frac{d E_{\text{sys}}}{dt} &= \dot{W}_{\text {electric, in}}-\dot{W}_{\text {shaft, out}}-\dot{Q}_{\text {out, ss}} \left[1-e^{-t /(20 \mathrm{~s})}\right] \\ &= (2.00 \mathrm{~kW})-(1.800 \mathrm{~kW})-(0.20 \mathrm{~kW}) \left[1-e^{-t /(20 \mathrm{~s})}\right] = (0.20 \mathrm{~kW}) e^{-t /(20 \mathrm{~s})} \end{aligned} \nonumber \] Así la tasa de cambio en el tiempo es mayor en\(t=0\) y luego disminuye exponencialmente.

Comentarios:

(1) La suposición de que la energía eléctrica y la potencia del eje son constantes durante este transitorio de arranque es probablemente incorrecta. Un modelo más preciso del motor requeriría una curva de rendimiento del motor que muestre el par y la corriente eléctrica en función de la velocidad de rotación. Por lo general, cuando un motor arranca, la corriente aumenta para proporcionar el par de arranque necesario. Una porción de la energía del sistema se almacenaría en la energía cinética rotacional del rotor a medida que gira hacia arriba.

(2) ¿Cómo funciona la energía dentro del sistema en función del tiempo? Para ello se debe integrar la tasa de cambio con el tiempo. ¿Cuál es el cambio máximo? ¿Hay uno? Pruébalo y mira lo que obtienes. Respuesta:\(\Delta E=(4.0 \mathrm{~kJ}) \left[1-e^{-t /(20 \mathrm{~s})}\right]\)

Ejemplo: compresor de refrigerante

Un sistema de refrigeración incluye un compresor que toma refrigerante en el Estado 1 y descarga el refrigerante en el Estado 2. La información del estado disponible se muestra en la figura. La entrada de energía al compresor es\(2.2 \mathrm{~kW}\). El caudal másico del refrigerante es\(0.014 \mathrm{~kg} / \mathrm{s}\).

Determine (a) la dirección y magnitud de la velocidad de transferencia de calor y (b) el par del eje si la potencia del compresor se suministra como trabajo del eje y el compresor opera en\(600 \mathrm{rpm}\).

Figura\(\PageIndex{4}\): Sistema de compresor de refrigerante, con toda la información conocida sobre los estados de entrada y salida del refrigerante.

Solución

Conocido: Un compresor opera en condiciones de estado estacionario.

Buscar: Determine la velocidad de transferencia de calor en estado estacionario y el par del eje para el compresor.

Dado: Información de estado, potencia y eje como se incluye en la declaración del problema anterior. [Estudiantes, esta información no se repite aquí porque está tan claramente señalada anteriormente; sin embargo, si estaban preparando una solución de ingeniería para el registro, deben utilizar este espacio para documentar toda la información y símbolos obtenidos del problema.]

Análisis:

Estrategia\(\rightarrow\) Nuevamente, ya que estamos hablando de energía, intente la conservación de energía y masa.
Sistema\(\rightarrow\) Tratar el compresor como un sistema abierto no deformante con una entrada y una salida
Propiedad\(\rightarrow\) Energía y masa (ya que es un sistema abierto) Intervalo de
tiempo Intervalo de tiempo\(\rightarrow\) Infinitesimal, forma de tasa

Comenzando con un diagrama del sistema que se muestra a continuación, tenemos una tasa de transferencia de calor en, una potencia de eje y dos lugares donde la masa cruza el límite del sistema.

Figura\(\PageIndex{5}\): Transferencias de masa y energía hacia/fuera del sistema compresor.

Escribiendo la forma de tasa del balance energético y el balance de masa para este sistema tenemos lo siguiente:

\[ \begin{aligned} & \text{Energy:} \quad\quad \underbrace{ \cancel{\frac{d E_{\text{sys}}}{dt}}^{=0} }_{\text {Steady state}} = \dot{W}_{\text {shaft, in}}+\dot{Q}_{\text {in}} + \dot{m}_{1}\left(h_{1}+\frac{V_{1}{ }^{2}}{2}+g z_{1}\right) - \dot{m}_{2}\left(h_{2}+\frac{V_{2}{ }^{2}}{2}+g z_{2}\right) \\ & \text{Mass:} \quad\quad \underbrace{ \cancel{\frac{d m_{\text {sys}}}{dt}}^{=0} }_{\text {Steady state}} = \dot{m}_{1}-\dot{m}_{2} \quad \rightarrow \quad \dot{m}_{1}=\dot{m}_{2}=\dot{m} \end{aligned} \nonumber \]

Combinando estos resultados y resolviendo para la tasa de transferencia de calor tenemos lo siguiente:

\[ \begin{gathered} 0 = \dot{W}_{\text{shaft, in}} + \dot{Q}_{\text{in}} + \dot{m}_{\text{in}} \left[ \left(h_{1}-h_{2}\right) + \left(\frac{V_{1}{ }^{2}}{2} - \frac{V_{2}{ }^{2}}{2}\right) + \underbrace{ g \cancel{ \left(z_{1}-z_{2}\right) }^{=0} }_{\begin{array}{c} \text{No information about} \\ \text{change in elevation given.} \\ \text{Assume this is negligible.} \end{array}} \right] \\ \dot{Q}_{\text{in}} = - \dot{W}_{\text{shaft, in}} - \dot{m}_{\text{in}} \left[\left(h_{1}-h_{2}\right) + \left(\frac{V_{1}{ }^{2}}{2} - \frac{V_{2}{ }^{2}}{2}\right) \right] \end{gathered} \nonumber \]

donde hemos reconocido explícitamente que no sabemos nada sobre el cambio de elevación y así hemos asumido que será insignificante. (No lo hemos olvidado. Hemos hecho conscientemente una suposición de modelado.)

(a) Ahora para resolver la transferencia de calor debemos sustituir la información de nuevo en el balance energético:

\[\begin{aligned} \dot{Q}_{\text{in}} &= -(2.2 \mathrm{~kW}) - \left(0.014 \frac{\mathrm{~kg}}{\mathrm{s}}\right) \left[(1449.8-1590.3) \ \frac{\mathrm{kJ}}{\mathrm{kg}} + \left(\frac{50^{2}-105^{2}}{2}\right) \left(\frac{\mathrm{m}}{\mathrm{s}}\right)^{2}\right] \\ &= -(2.2 \mathrm{~kW}) - \left(0.014 \ \frac{\mathrm{kg}}{\mathrm{s}}\right) \left[(-140.5) \ \frac{\mathrm{kJ}}{\mathrm{kg}} + (-4262.5) \frac{\mathrm{m}^{2}}{\mathrm{~s}^{2}} \times \left(\frac{1 \mathrm{~kJ}}{1000 \mathrm{~N} \cdot \mathrm{m}}\right) \times \left(\frac{1 \mathrm{~N}}{ \dfrac{\mathrm{~kg} \cdot \mathrm{m}}{\mathrm{s}^{2}} }\right)\right] \\ &= -(2.2 \mathrm{~kW})-\underbrace{\left(0.014 \ \frac{\mathrm{kg}}{\mathrm{s}}\right) \left[(-140.5) \ \frac{\mathrm{kJ}}{\mathrm{kg}} + (-4.2625) \ \frac{\mathrm{kJ}}{\mathrm{kg}}\right]}_{-2.027 \mathrm{~kW}} \\ &= -0.173 \mathrm{~kW} \end{aligned} \nonumber \]

Por lo tanto, la tasa de transferencia de calor para el compresor está\(0.173 \mathrm{~kW}\) fuera del sistema. Por lo general, se podría decir “el compresor pierde energía por transferencia de calor a razón de”\(0.173 \mathrm{~kW}\).

(b) Ahora para encontrar el par del eje tenemos que mirar la potencia del eje y aplicar la definición de potencia del eje:\[\begin{aligned} \dot{W}_{\text {shaft, in}} = \tau \cdot \omega \quad \rightarrow \quad \tau &= \frac{\dot{W}_{\text {shaft, in}}}{\omega} = \frac{2.2 \mathrm{~kW}}{600 \mathrm{~rpm}} \times \frac{\left(\frac{1 \mathrm{~kN} \cdot \mathrm{m}}{\mathrm{s} \cdot \mathrm{kJ}}\right)}{\left(\dfrac{\mathrm{rev} / \mathrm{min}}{\mathrm{rpm}}\right) \times \left(\dfrac{2 \pi \mathrm{~rad}}{\mathrm{rev}}\right)} \\ &= \frac{\left(2.2 \ \dfrac{\mathrm{kN} \cdot \mathrm{m}}{\mathrm{s}}\right)}{\left(1200 \pi \ \dfrac{\mathrm{rad}}{\mathrm{min}}\right)} \times \left(\frac{60 \mathrm{~s}}{\mathrm{~min}}\right) = 0.0350 \mathrm{~kN} \cdot \mathrm{m} = 35.0 \mathrm{~N} \cdot \mathrm{m} \end{aligned} \nonumber \] El par del eje aplicado al compresor tendrá el mismo sentido que la dirección de rotación del eje.

Comentar

(1) Observe cómo hemos indicado explícitamente nuestros supuestos a medida que pasamos de la forma más general de las ecuaciones de conservación a la forma específica de la ecuación utilizada para modelar este sistema.

(2) Típicamente, las únicas propiedades en los estados 1 y 2 que podríamos haber medido serían\(P\),\(T\), y\(V\). Todas las demás propiedades se habrían encontrado a partir de tablas o ecuaciones que se relacionan\(u\),\(h\), y\(\upsilon\) a\(P\) y\(T\).

Ejemplo — Separador de vapor

La mayoría de las centrales eléctricas de vapor tienen un dispositivo que separa el vapor (agua gaseosa) del agua líquida antes de que entre en la turbina de vapor. La siguiente figura muestra un ejemplo. La experiencia ha demostrado que las gotas de agua líquida, incluso las pequeñas, pueden erosionar significativamente las palas en una turbina de vapor.

Una mezcla de agua líquida y vapor ingresa a un recipiente separador a 1 con un caudal másico de\(10,000 \mathrm{~lbm} / \mathrm{h}\). El vapor sale del recipiente en 2 y el agua líquida sale del recipiente a las 3. El separador opera adiabáticamente en condiciones de estado estacionario con cambios insignificantes en la energía potencial cinética y gravitacional. Las mediciones en el recipiente indican que cuando el sistema está operando en\(2000 \mathrm{~psia}\), las entalpías específicas y los volúmenes específicos de las tres corrientes son los siguientes:\[\begin{array}{lll} h_{1}=787.7 \mathrm{~Btu} / \mathrm{lbm}; & h_{2}=1136.1 \mathrm{~Btu} / \mathrm{lbm}; & h_{3}=671.6 \mathrm{~Btu} / \mathrm{lbm}; \\ \mathrm{\upsilon}_{1}=0.0662 \mathrm{~ft}^{3} / \mathrm{lbm}; & \mathrm{v}_{2}=0.1881 \mathrm{~ft}^{3} / \mathrm{lbm}; & \mathrm{v}_{3}=0.02563 \mathrm{~ft}^{3} / \mathrm{lbm} \end{array} \nonumber \]

Figura\(\PageIndex{6}\): Separador de vapor con tres aberturas.

Determinar (a) los caudales másicos a 2 y 3, y (b) las áreas de flujo a 1 y 3 asumiendo que la velocidad es\(15 \mathrm{~ft} / \mathrm{s}\).

Solución

Conocido: Un separador de vapor opera en condiciones adiabáticas de estado estacionario.

Encuentre: (a) Caudales másicos que salen del recipiente
(b) Velocidades del fluido en todas las secciones transversales del flujo asumiendo una\(15 \mathrm{~ft} / \mathrm{s}\) velocidad.

Dado: Ver figura anterior.

Análisis:

Estrategia\(\rightarrow\) Intentar la conservación de la masa.
Sistema\(\rightarrow\) Tome el recipiente como un sistema abierto no deformante.
Propiedad para contar\(\rightarrow\) Masa Intervalo de
tiempo Intervalo\(\rightarrow\) infinitesimal, forma de tasa

Figura\(\PageIndex{7}\): Límite del sistema y la masa fluye a través de él.

Al esbozar el diagrama del sistema, tenemos tres flujos másicos cruzando el límite del sistema como se muestra en el boceto. Ahora escribiendo las ecuaciones para la conservación de la masa, tenemos lo siguiente:

\[\text {Mass:} \quad\quad \underbrace{ \cancel{\frac{dm_{\text{sys}}}{dt}}^{=0} }_{\text {Steady-state}} = \dot{m}_{1}-\dot{m}_{2}-\dot{m}_{3} \quad \rightarrow \quad \dot{m}_{3}=\dot{m}_{1}-\dot{m}_{2} \nonumber \]

Desafortunadamente hay dos incógnitas, así que necesitamos otra ecuación. (Observe que nuestra estrategia está siendo revisada a medida que trabajamos, ya que no nos dimos cuenta de que la conservación de la masa nos daría una ecuación con dos incógnitas.) Para obtener otra ecuación, aplique la conservación de energía a este sistema:\[ \text{Energy:} \quad\quad \underbrace{ \cancel{\frac{d E_{\text{sys}}}{d t}}^{=0} }_{\text {Steady state}} = \underbrace{ \cancel{ \dot{Q}_{\text {net, in}} }^{=0}}_{\text {Adiabatic}} + \underbrace{ \cancel{ \dot{W}_{\text {net, in}} }^{=0}}_{\begin{array}{c}\text {Nothing on boundary} \\ \text {looks like power}\end{array}} + \underbrace{\dot{m}_{1} h_{1}-\dot{m}_{2} h_{2}-\dot{m}_{3} h_{3}}_{\begin{array}{c} \text {Neglecting kinetic and potential} \\ \text {energy per the problem statement}\end{array}} \quad \rightarrow \quad 0=\dot{m}_{1} h_{1}-\dot{m}_{2} h_{2}-\dot{m}_{3} h_{3} \nonumber \]

La ecuación energética tiene las mismas dos incógnitas: los caudales másicos en 2 y 3. Sustituir en los valores de la declaración del problema y resolver simultáneamente da lo siguiente:\[\left. \begin{array}{l} \dot{m}_{3}=\left(10000 \ \dfrac{\mathrm{lbm}}{\mathrm{h}}\right)-\dot{m}_{2} \\ 0=\left(10000 \ \dfrac{\mathrm{lbm}}{\mathrm{h}}\right) \left(778.7 \ \dfrac{\mathrm{Btu}}{\mathrm{lbm}}\right) - \dot{m}_{2}\left(1136.1 \ \dfrac{\mathrm{Btu}}{\mathrm{lbm}}\right) - \dot{m}_{3}\left(671.6 \ \dfrac{\mathrm{Btu}}{\mathrm{lbm}}\right) \end{array} \right\} \quad \rightarrow \quad \left\{ \begin{array}{l} \dot{m}_{2}=2.50 \times 10^{3} \mathrm{~lbm} / \mathrm{h} \\ \dot{m}_{3}=7.50 \times 10^{3} \mathrm{~lbm} / \mathrm{h} \end{array}\right. \nonumber \] Así que aproximadamente\(25 \%\) del agua entrante sale del recipiente como vapor y\(75 \%\) sale del recipiente como agua líquida.

Ahora para encontrar las áreas de sección transversal si la velocidad es\(15 \mathrm{~ft} / \mathrm{s}\), podemos hacer uso de la definición de caudal másico de la siguiente manera:\[\begin{aligned} &\dot{m}=\rho V A_{c} = \frac{V A_{c}}{\upsilon} \rightarrow A_{c}=\frac{\dot{m} \upsilon}{V} = \frac{\dot{m} \upsilon}{\left(15 \ \dfrac{\mathrm{ft}}{\mathrm{s}} \times \dfrac{3600 \mathrm{~s}}{\mathrm{~h}}\right)} = \frac{\dot{m} \upsilon}{\left(54000 \ \dfrac{\mathrm{ft}}{\mathrm{h}}\right)} \\ & \text {At 1:} \quad A_{c, \ 1} = \frac{\left(10,000 \ \dfrac{\mathrm{lbm}}{\mathrm{h}}\right) \left(0.0662 \ \dfrac{\mathrm{ft}^{3}}{\mathrm{lbm}}\right)}{\left(54000 \ \dfrac{\mathrm{ft}}{\mathrm{h}}\right)} = 12.3 \times 10^{-3} \ \mathrm{ft}^{2}=1.77 \ \mathrm{in}^{2} \\ & \text {At 3:} \quad A_{c, \ 3} = \frac{\left(7500 \ \dfrac{\mathrm{lbm}}{\mathrm{h}}\right) \left(0.02563 \ \dfrac{\mathrm{ft}^{3}}{\mathrm{lbm}}\right)}{\left(54000 \ \dfrac{\mathrm{ft}}{\mathrm{h}}\right)} = 3.56 \times 10^{-3} \ \mathrm{ft}^{2}=0.513 \ \mathrm{in}^{2} \end{aligned} \nonumber \] Observe cómo el área en\(3\) es aproximadamente\(30 \%\) del área en\(1\), aunque el caudal másico sea solo\(77 \%\) del caudal másico en \(1\). Este es el resultado de los cambios en el volumen específico del fluido.

Comentarios

(1) Observe cómo en este problema nos vimos obligados a utilizar tanto la energía como los balances de masa para obtener ecuaciones suficientes para resolver el problema. A menudo nuestra estrategia inicial será incorrecta. Un sello distintivo de un buen problema resuelto es la capacidad de no quedar encerrado en un solo enfoque. Sea flexible.

(2) Si no se hubiera dado el caudal másico entrante, aún podríamos haber resuelto la división del flujo másico en el separador. Para ello, dividimos tanto las ecuaciones de masa como de energía por uno de los tres caudales desconocidos, digamos el caudal másico a 1:\[\begin{array}{c} 0 = \dot{m}_{1}-\dot{m}_{2}-\dot{m}_{3} \\ 0=\dot{m}_{1} h_{1}-\dot{m}_{2} h_{2}-\dot{m}_{3} h_{3} \end{array} \quad \rightarrow \quad \begin{array}{c} 0=1-\dfrac{\dot{m}_{2}}{\dot{m}_{1}}-\dfrac{\dot{m}_{3}}{\dot{m}_{1}} \\ 0=h_{1} - \left(\dfrac{\dot{m}_{2}}{\dot{m}_{1}}\right) h_{2}-\left(\dfrac{\dot{m}_{3}}{\dot{m}_{1}}\right) h_{3} \end{array} \nonumber \] De esta manera, hemos pasado de tres incógnitas a dos incógnitas y ahora tenemos ecuaciones suficientes para resolver para la división. Los problemas del sistema abierto a menudo se resuelven sobre una base “por unidad de masa” dividiendo todo en la ecuación por un caudal másico y eliminando uno desconocido.

Ejemplo — Hacer las rondas

Un gas está contenido dentro de un dispositivo simple de cilindro de pistón e inicialmente ocupa un volumen de\(0.020 \mathrm{~m}\) y a una presión de\(1.0 \mathrm{~MPa}\). El gas ejecuta tres procesos en serie y vuelve a su estado inicial como se describe a continuación:

Estado 1:\(P_{1}=1.0 \mathrm{~MPa}, V\kern-0.8em\raise0.3ex-_{1}=0.020 \mathrm{~m}^{3}\)

Proceso 1\(\rightarrow\) 2: Expansión politrópica con\(P V\kern-1.0em\raise0.3ex-^{1.4}=C\)

Estado 2:\(V\kern-1.0em\raise0.3ex-_{2} = 2 V\kern-0.8em\raise0.3ex-_{1}\)

Proceso 2\(\rightarrow\) 3: Calentamiento de volumen constante

Estado 3:\(P_{3}=P_{1}, \quad V\kern-1.0em\raise0.3ex-_{3} = V\kern-0.8em\raise0.3ex-_{2}\)

Proceso 3:\(\rightarrow\) 1: Compresión constante

(Esto se llama ciclo termodinámico porque el sistema ejecuta una serie de procesos y luego vuelve a su estado inicial). Supongamos que los cambios en la energía cinética y potencial gravitacional son insignificantes para todos los procesos.

Figura\(\PageIndex{8}\): Sistema que consiste en el gas dentro de un dispositivo de cilindro y pistón.

Determinar (a) el trabajo realizado en el gas dentro del pistón para cada proceso; (b) el trabajo neto para todo el ciclo, es decir, suma del trabajo para cada proceso en el ciclo; (c) la transferencia de calor para todo el ciclo.

Solución

Conocido: Un gas contenido en un dispositivo de pistón-cilindro ejecuta un ciclo de tres procesos.

Encontrar: (a) trabajo realizado en el gas para cada proceso
(b) trabajo neto realizado en el gas para el ciclo.
(c) transferencia neta de calor para todo el ciclo.

Dado: Ver figura e información de estado/proceso arriba.

Análisis:

Estrategia\(\rightarrow\) Debe requerir el uso de conservación de energía y puede ser capaz de utilizar la definición de\(\mathrm{PdV}\) trabajo para evaluar el trabajo para al menos algunos de los procesos.
Sistema\(\rightarrow\) Cerrado, sistema deformante que consiste en el gas en el cilindro (ver línea discontinua)
Propiedad a contar\(\rightarrow\) Energía Intervalo de
tiempo\(\rightarrow\) Debe ser tiempo finito ya que cada proceso tiene un comienzo y un final definidos.

a) El único tipo de trabajo que es posible para este sistema es el\((\mathrm{PdV})\) trabajo de compresión-expansión. Suponiendo que cada proceso ocurre lo suficientemente lento como para que la presión sea uniforme dentro del gas a lo largo del proceso tenemos la siguiente ecuación:\[W_{\text{PdV, in}} = -\int\limits_{1}^{2} P \ d V\kern-0.8em\raise0.3ex- \nonumber \] El truco entonces es evaluarlo para cada proceso según se requiera.

Proceso\(1 \rightarrow 2\): Proceso politrópico con\(P V\kern-1.0em\raise0.3ex-^{1.4} =C\). Integrando sujeto a esta restricción, tenemos

\[ \begin{aligned} W_{1-2, \text{ in}} &= - \int\limits_{1}^{2} P \ d V\kern-1.0em\raise0.3ex- = - \int\limits_{V\kern-0.5em\raise0.3ex-_{1}}^{V\kern-0.5em\raise0.3ex-_{2}} \frac{C}{V\kern-0.8em\raise0.3ex-^{1.4}} \ d V\kern-1.0em\raise0.3ex- = -C \int\limits_{V\kern-0.5em\raise0.3ex-_{1}}^{V\kern-0.5em\raise0.3ex-_{2}} V\kern-1.0em\raise0.3ex-^{1.4} \ d V\kern-1.0em\raise0.3ex- = -C\left[ \frac{1}{-1.4+1} V\kern-1.0em\raise0.3ex-^{(-1.4+1)}\right]_{V\kern-0.5em\raise0.3ex-_{1}}^{V\kern-0.5em\raise0.3ex-_{2}} = \frac{C}{1.4-1} \left[V\kern-1.0em\raise0.3ex-_{2}{ }^{-0.4} - V\kern-1.0em\raise0.3ex-_{1}{ }^{-0.4}\right] \\ &= \frac{\left(P_{1} V\kern-1.0em\raise0.3ex-_{1}{ }^{1.4}\right)}{0.4} \left(V\kern-1.0em\raise0.3ex-_{1}{ }^{-0.4}\right) \left[ \left(\frac{V\kern-0.8em\raise0.3ex-_{2}}{V\kern-0.8em\raise0.3ex-_{1}}\right)^{-0.4} - 1\right] = 2.5 \left(P_{1} V\kern-1.0em\raise0.3ex-_{1}\right) \left[ \left(\frac{V\kern-0.8em\raise0.3ex-_{2}}{V\kern-0.8em\raise0.3ex-_{1}}\right)^{-0.4} - 1\right] \\ &= 2.5 \left[\left(1000 \mathrm{~kPa}\right) \left(0.020 \mathrm{~m}^{3}\right)\right] \left[\left(\frac{2}{1}\right)^{-0.4} - 1\right] = \left(-12.1 \mathrm{~kPa} \cdot \mathrm{m}^{3}\right) \times \left( \frac{\mathrm{N} / \mathrm{m}^{3}}{\mathrm{Pa}} \right) = -12.1 \mathrm{~kN} \cdot \mathrm{m} \end{aligned} \nonumber \]

Proceso 2\(\rightarrow\) 3: Calentamiento de volumen constante

Ya que no hay cambio de volumen y el\(\mathrm{PdV}\) trabajo es el único tipo posible aquí,\(W_{2-3, \text { in}}=0\).

Proceso 3\(\rightarrow\) 1: Enfriamiento a presión constante\[W_{3-1, \text { in}} = -\int\limits_{3}^{1} P \ d V\kern-0.8em\raise0.3ex- = -P_{3} \left(V\kern-1.0em\raise0.3ex-_{1} - V\kern-0.8em\raise0.3ex-_{3}\right) = -P_{3} \left(V\kern-1.0em\raise0.3ex-_{1} - V\kern-0.8em\raise0.3ex-_{2}\right) \quad \text { because } V\kern-0.8em\raise0.3ex-_{3} = V\kern-0.8em\raise0.3ex-_{2} \nonumber \]

Pero ya lo sabemos para el Estado 2\(V\kern-0.8em\raise0.3ex-_{2} = 2 V\kern-0.8em\raise0.3ex-_{1}\). Combinar esto nos da el trabajo para el proceso 3\(\rightarrow\) 1:\[W_{3-1, \text { in}} = -P_{3} \left(V\kern-1.0em\raise0.3ex-_{1} - V\kern-0.8em\raise0.3ex-_{2}\right) = -(1000 \mathrm{~kPa})(0.020-0.040) \mathrm{~m}^{3} = 20.0 \mathrm{~kN} \cdot \mathrm{m} \nonumber \]

b) Para encontrar el trabajo neto para el ciclo solo sumamos los tres términos de trabajo:\[W_{\text {cycle, net in}} = W_{1-2, \text { in}} + W_{2-3, \text { in}} + W_{3-1, \text { in}} = [(-12.1)+0+20.0] \mathrm{~kN} \cdot \mathrm{m} = 7.9 \mathrm{~kN} \cdot \mathrm{m} = 7.9 \mathrm{~kJ} \nonumber \]

(c) Para encontrar la transferencia neta de calor de energía, recurriremos al balance energético de tiempo finito para un sistema cerrado\[\begin{array}{l} \quad\,\,\ \text{ Process } 1 \rightarrow 2: \quad \Delta E = E_{2}-E_{1} = Q_{1-2, \text { in}}+W_{1-2, \text { in}} \\ \quad\,\,\ \text{ Process } 2 \rightarrow 3: \quad \Delta E = E_{3}-E_{2} = Q_{2-3, \text { in}}+W_{2-3, \text { in}} \\ \underline{ +\quad \text {Process } 3 \rightarrow 1: \quad \Delta E = E_{1}-E_{3} = Q_{3-1, \text{ in}}+W_{3-1, \text{ in}} } \\ \underbrace{\left(E_{2}-E_{1}\right) + \left(E_{3}-E_{2}\right) + \left(E_{1}-E_{3}\right)}_{=0} = \underbrace{\left(Q_{1-2, \text { in}} + Q_{2-3, \text { in}} + Q_{3-1, \text { in}}\right)}_{Q_{\text {cycle, net in}}} + \underbrace{\left(W_{1-2, \text { in}}+W_{2-3, \text { in}}+W_{3-1, \text { in}}\right)}_{W_{\text {cycle, net in}}} \end{array} \nonumber \]

Así tenemos\(0=Q_{\text {cycle, net in}} + W_{\text {cycle, net in}}\)

Y para la tasa neta de transferencia de calor para el ciclo tenemos\(Q_{\text {cycle, net in}} = -W_{\text {cycle, net in}}=7.9 \mathrm{~kJ}\)

Comentar

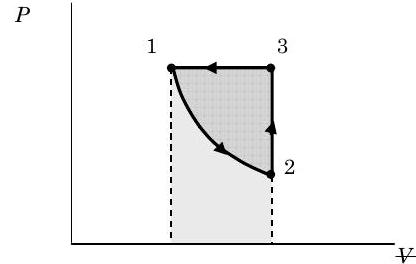
En la siguiente figura se muestran las diversas áreas que corresponden al trabajo para los diversos procesos. El rectángulo bajo la línea 3-1 representa el trabajo para el Proceso 3\(\rightarrow\) 1 y el área bajo la curva 1-2 representa el trabajo para el Proceso 1\(\rightarrow\) 2. El área encerrada dentro de la curva cerrada 1-2-3 representa el trabajo neto para el ciclo. Si hubiéramos invertido la dirección del ciclo, ¿cómo\(W\) cambiarían los valores de\(Q\) y para el ciclo?

Figura\(\PageIndex{9}\): Gráfica de presión contra volumen para el gas a medida que se somete a los tres procesos.

Ejemplo — Dicen que hay resistencia

Una batería automática de 12 voltios está conectada a una\(100 \text{ k} \Omega \ (100 \text{ kilo-ohm})\) resistencia. Supongamos que los cambios en la energía potencial cinética y gravitacional son insignificantes y que el voltaje y la corriente de la batería no cambian con el tiempo para el periodo de este problema. Las mediciones indican que la tasa de transferencia de calor de la batería es aproximadamente\(2 \%\) de la energía eléctrica que entrega.

Figura\(\PageIndex{10}\): Batería conectada a una resistencia de 100 kilo-ohmios.

Determinar: (a) la tasa de cambio de la energía interna de la batería, en\(\mathrm{J} / \mathrm{s}\); (b) la tasa de transferencia de calor para la resistencia, en vatios.

Solución

Conocido: Una batería de automóvil de 12 voltios está conectada a una\(100-\mathrm{k} \Omega\) resistencia

Encuentra: (a) Tasa de cambio de la energía interna de la batería, en\(\mathrm{kJ} / \mathrm{s}\).
(b) Velocidad de transferencia de calor para la resistencia, pulg\(\mathrm{kW}\).

Para la batería:

\(\dot{Q}_{\text {battery, out}}=(0.02) \cdot \dot{W}_{\text {battery, out}}\)

\(V^{+}-V^{-}=12 \text{ volts}\)

Para la resistencia:\(R=100 \mathrm{~k} \Omega\)

Figura\(\PageIndex{11}\): Separación del circuito en sistemas para análisis.

Análisis:

Estrategia\(\rightarrow\) Debido a que nos interesan los cambios internos de energía y la transferencia de calor, intente conservar la energía.
\(\rightarrow\)Es posible que el sistema necesite usar batería y resistencia.
Propiedad para contar\(\rightarrow\) Energía.
Intervalo de tiempo Intervalo de tiempo\(\rightarrow\) infinitesimal, forma de tasa de ecuaciones.

Antes de que podamos resolver para cualquier otra información, necesitaremos conocer la corriente eléctrica que fluye en el sistema. Asumiendo que la resistencia obedece a la Ley de Ohm, entonces\[\Delta V = i R \quad \rightarrow \quad i=\frac{\Delta V}{R} = \frac{(12 \mathrm{~V})}{\left(100 \times 10^{3} \ \Omega\right)} \times \left(\frac{1 \mathrm{~A} \cdot \Omega}{\mathrm{V}}\right) = 12 \times 10^{-5} \mathrm{~A}=0.12 \mathrm{~mA} \nonumber \]

Ahora para responder a la parte (a), consideremos un sistema que incluya la batería y algunos de los cables como se muestra arriba. Aplicando el balance energético a este sistema cerrado tenemos\[\underbrace{ \cancel{\frac{d E_{\text{sys}}}{dt}}^{=U} }_{\begin{array}{c} \text {Neglecting all} \\ \text {but internal energy} \end{array}} = -\dot{W}_{\text{out}} - \cancel{ \dot{Q}_{\text{out}} }^{=0.02 \dot{W}_{\text {out}}} \quad \rightarrow \quad \frac{d U_{\text{battery}}}{dt} = -\dot{W}_{\text {out}} - 0.02 \dot{W}_{\text {out}} = -1.02 \cdot \dot{W}_{\text {out}} \nonumber \]

Para continuar se requiere usar nuestra definición de energía eléctrica de la siguiente manera:\[\begin{aligned} \frac{d U_{\text {battery}}}{d t} &= (-1.02) \cdot \dot{W}_{\text {electric, out}} = (-1.02) \cdot(i \Delta V) \\ &=(-1.02) \cdot[(0.12 \mathrm{~mA}) \cdot (12 \text { volts})] = (-1.02) \cdot \underbrace{\left[1.44 \times 10^{-3} \mathrm{~W}\right]}_{\dot{W}_{\text {battery, out}}} = -1.47 \times 10^{-3} \ \frac{\mathrm{J}}{\mathrm{s}} \end{aligned} \nonumber \]

Observe que a pesar de que la batería tiene una diferencia de voltaje constante y una corriente constante, no es un sistema de estado estacionario. Esto debería tener sentido físico ya que la batería está suministrando energía a otro sistema; así, su energía interna debería estar disminuyendo.

Para la parte b) tenemos dos opciones en este punto. Podemos usar un sistema que rodee la resistencia o uno que abarque la batería, los cables y la resistencia. Vamos a mostrar ambos para la comparación de dos enfoques alternos:

\(\text{System} = \text{Resistor}\)

\(\text{System} = \text{Battery} + \text{Resistor} + \text{Wires}\)

\ (\ text {Sistema} =\ text {Resistor}\)” class="lt-eng-81507">\[ \begin{aligned} \underbrace{ \cancel{\frac{d E_{\text{sys}}}{dt}}^{=0} }_{\begin{array}{c} \text{Assume} \\ \text{steady-state} \end{array}} &= \dot{Q}_{\text{Resistor, in}} + \dot{W}_{\text{Resistor, in}} \\ 0 &= \dot{Q}_{\text{Resistor, in}} + \dot{W}_{\text{Resistor, in}} \\ -\dot{Q}_{\text{Resistor, in}} &= \dot{W}_{\text{Resistor, in}} \\ &= \dot{W}_{\text{Battery, out}} = 1.44 \mathrm{~mW} \\ { } \\ \dot{Q}_{\text{Resistor, out}} &= -\dot{Q}_{\text{Resistor, in}} = 1.44 \mathrm{~mW} \end{aligned} \nonumber \]

\ (\ text {Sistema} =\ text {Batería} +\ text {Resistor} +\ text {Cables}\)” class="lt-eng-81507">\[ \begin{aligned} \frac{d E_{\text{sys}}}{dt} &= \dot{Q}_{\text{net, in}} + \underbrace{\cancel{ \dot{W}_{\text{net, in}} }^{=0}}_{\begin{array}{c} \text{No work found} \\ \text{in this system} \end{array}} \\ \cancel{ \frac{d E_{\text{Battery}}}{dt} }^{=U} + \underbrace{ \cancel{ \frac{d E_{\text{Wires}}}{dt} }^{=0} + \cancel{ \frac{d E_{\text{Resistor}}}{dt} }^{=0} }_{\begin{array}{c} \text{Assume no change in } E \\ \text{or steady state} \end{array}} &= \dot{Q}_{\text{Battery, in}} + \underbrace{ \cancel{\dot{Q}_{\text{Wires, in}}}^{=0} }_{\begin{array}{c} \text{Assumed} \\ \text{negligible} \end{array}} + \dot{Q}_{\text{Resistor, in}} \\ \frac{d U_{\text{Battery}}}{dt} &= \dot{Q}_{\text{Battery, in}} + \dot{Q}_{\text{Resistor, in}} \\ \underbrace{ \frac{d U_{\text{Battery}}}{dt} - \dot{Q}_{\text{Battery, in}} }_{\dot{W}_{\text{Battery, in}}} &= \dot{Q}_{\text{Resistor, in}} \\ { } \\ \dot{Q}_{\text{Resistor, in}} &= \dot{W}_{\text{Battery, in}} = -1.44 \mathrm{~mW} \end{aligned} \nonumber \]

Independientemente del sistema que seleccionemos para nuestro análisis, deberíamos obtener la misma respuesta si estamos haciendo suposiciones consistentes para ambos sistemas.

Comentarios:

(1) En este problema, tuvimos que elegir un par de sistemas diferentes para desarrollar toda la información que necesitábamos para resolver el problema. Un sello distintivo de un buen solucionador de problemas es la capacidad de buscar y usar diferentes sistemas según corresponda para resolver un problema. A menudo descubrirás que seleccionar un sistema en particular conduce a una solución muy difícil o a una solución con supuestos “riesgosos”. En este caso, deberías mirar a tu alrededor y ver si puedes encontrar un mejor sistema.

(2) Imagínese que habíamos conectado la batería a la resistencia hacia atrás, es decir, con corriente fluyendo en dirección opuesta. ¿Cómo cambiarían las respuestas? El flujo de corriente a través de la resistencia es un ejemplo de un proceso internamente irreversible. En breve descubriremos que los procesos irreversibles y reversibles juegan un papel clave en el establecimiento de límites importantes en nuestra capacidad de transferir y convertir energía.