6.1: Relaciones constitutivas y de gobierno

Las olas superficiales en el agua son un excelente ejemplo de un proceso aleatorio estacionario y ergódico. El modelo de olas como superposición casi lineal de componentes armónicos, en fase aleatoria, se confirma por mediciones en el mar, así como por la teoría lineal de las olas, tema de esta sección. Saltaremos algunos elementos de la mecánica de fluidos donde corresponda, y nos moveremos rápidamente a los casos de flujo bidimensional, inviscido e irrotacional. Estas son las principales suposiciones que permiten el modelo de onda lineal.

Primero, sabemos que cerca de la superficie del mar, el agua puede considerarse como incompresible, y que la densidad\(\rho\) es casi uniforme. En este caso, una forma simple de conservación de la masa sostendrá:

\[ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} = 0; \]

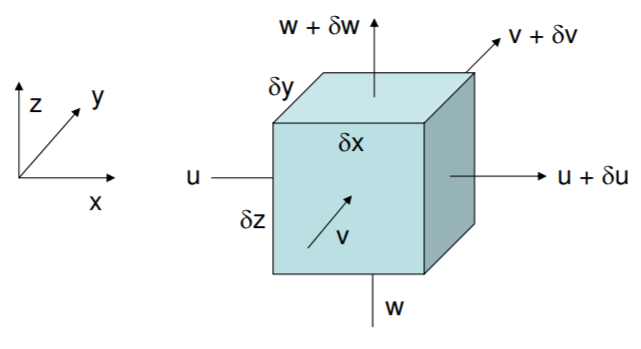
donde está el espacio cartesiano\([x, \, y, \, z]\), con vectores de velocidad de partículas respectivos\([u, \, v, \, w]\). En palabras, la ecuación anterior dice que el flujo neto hacia un volumen diferencial tiene que ser igual al flujo neto que sale de él. Considerando una caja de dimensiones\( [\delta x, \, \delta y, \, \delta z] \), vemos que cualquiera\(\delta u\) a través de la\(x\) -dimensión tiene que ser contabilizada por\(\delta v\) y\(\delta w\):

\[ \delta u\, \delta y\, \delta z + \delta v\, \delta z\, \delta z + \delta w\, \delta x\, \delta y = 0. \]

Figura\(\PageIndex{1}\): ilustra la relación entre el sistema de coordenadas cartesianas tridimensionales y sus vectores unitarios asociados.

A continuación, invocamos la ley de Newton, en las tres direcciones:

\ begin {align}\ rho\ left [\ dfrac {\ u parcial} {\ t parcial} + u\ dfrac {\ u parcial} {\ parcial x} + v\ dfrac {\ u parcial} {\ parcial y} + w\ dfrac {\ u parcial} {\ z parcial}\ derecha]\, &=\, -\ dfrac {\ p parcial} {\ parcial x} +\ mu\ izquierda [\ dfrac {\ parcial^2 u} {\ parcial x^2} +\ dfrac {\ parcial^2 u} {\ parcial y^2} +\ dfrac {\ parcial^2 u} {\ parcial z^2}\ derecha];\\ [4pt]\ rho\ izquierda [\ dfrac {\ parcial v} {\ parcial t} + v\ dfrac {\ parcial v} {\ parcial x} + w\ dfrac {\ parcial v} {\ parcial y} + u\ dfrac {\ parcial v} {\ parcial z}\ derecha]\, &=\, -\ dfrac {\ parcial p} {\ parcial y} +\ mu\ izquierda [\ dfrac {\ parcial^2 v} {\ parcial x^2} +\ dfrac {\ parcial^2 v } {\ parcial y^2} +\ dfrac {\ parcial^2 v} {\ parcial z^2}\ derecha];\\ [4pt]\ rho\ izquierda [\ dfrac {\ w parcial} {\ t parcial} + w\ dfrac {\ parcial w} {\ parcial x} + u\ dfrac {\ parcial w} {\ parcial y} + v\ {\ parcial w} {\ z parcial}\ derecha]\, &=\, -\ dfrac {\ parcial p} {\ z parcial} +\ mu\ izquierda [\ dfrac {\ parcial^2 x} {\ parcial x^2} +\ dfrac {\ parcial^2 w} {\ parcial y^2}\ dfrac {\ parcial^2 w} {\ parcial z^2}\ derecha] -\ rho g.\ end {align}

Aquí el lado izquierdo de cada ecuación es la aceleración de la partícula de fluido, a medida que se mueve a través del volumen diferencial. Los términos como\(u \frac{\partial u}{\partial x}\) capturan el hecho de que el equilibrio de fuerzas es para una partícula en movimiento; la expansión de la regla de la cadena va así en la\(x\) dirección -dirección:

\[ \dfrac{du}{dt} = \dfrac{\partial u}{\partial t} + \dfrac{\partial u}{\partial x} \dfrac{\partial x}{\partial t} + \dfrac{\partial u}{\partial y} \dfrac{\partial y}{\partial t} + \dfrac{\partial u}{\partial z} \dfrac{\partial z}{\partial t}, \]

dónde\(u = \partial x / \partial t\) y así sucesivamente.

En el lado derecho de las tres ecuaciones de equilibrio de fuerzas anteriores, la presión diferencial actúa claramente para ralentizar la partícula (de ahí el signo negativo), y la fricción viscosa se aplica a través de la viscosidad absoluta\(\mu\). La tercera ecuación también tiene un término para gravedad, llevando en el caso de velocidades cero a la relación familiar\(p(z) = - \rho g z\), donde\(z\) se toma positiva hacia arriba desde la superficie libre media.