7.4: Programación lineal

Última actualización
Guardar como PDF

Page ID: 84133

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

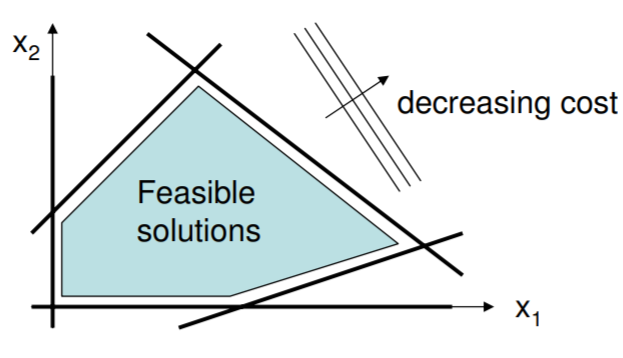
Consideramos ahora el caso de que el costo es una función lineal de\(n\) parámetros. Claramente no hay solución a menos que el espacio de parámetros esté restringido, y de hecho se garantiza que la solución esté en el límite. La situación está bien ilustrada en dos dimensiones\((n = 2)\), un ejemplo de las cuales se muestra a continuación. Aquí se muestran cinco límites lineales de desigualdad; no\(x\) se permiten fuera de la región factible. En el caso general, pueden estar presentes restricciones tanto de igualdad como de desigualdad.

Gráfico que muestra una región bidimensional delimitada por 5 desigualdades lineales, dentro de las cuales debe encontrarse la solución. — Figura\(\PageIndex{1}\): gráfica de una región bidimensional delimitada por 5 desigualdades lineales, donde el costo es una función lineal de los dos parámetros indicados en los ejes. Si bien el costo puede ser más óptimo fuera de la región delimitada, todas las soluciones factibles deben estar dentro de esta región.

La naturaleza del problema -todo lineal, y que comprende la desigualdad y posiblemente restricciones de igualdad- admite algoritmos especiales y potentes que son efectivos incluso en dimensiones muy altas, por ejemplo, en miles. En dimensiones inferiores, podemos apelar a la intuición obtenida de la figura para construir un método más sencillo para sistemas pequeños, digamos hasta diez incógnitas.

Ante todo, queda claro a partir de la figura que la solución tiene que estar en uno de los límites. De hecho, la solución se encuentra en un vértice de\(n\) hipersuperficies de dimensión\(n-1\). Tal hipersuperficie es una línea en el espacio bidimensional, un plano en tres espacios, y así sucesivamente. Diremos que una línea en tres espacios es una intersección de dos planos, y por lo tanto equivale a dos hipersuperficies de dimensión dos. Se puede verificar que una hipersuperficie de dimensión\(n-1\) se define con una ecuación.

Si no hay restricciones de igualdad, entonces estas\(n\) hipersuperficies que forman el vértice de la solución son un subconjunto de las restricciones de\(I\) desigualdad. Generalmente vamos a tener\(I>n\). Si también hay restricciones de\(E<n\) igualdad, entonces la solución radica en la intersección de estas hipersuperficies de\(E\) igualdad y\(n-E\) otras hipersuperficies tomadas de las restricciones de\(I\) desigualdad. Por supuesto, si\(E=n\), entonces sólo tenemos un sistema lineal que resolver. Así tenemos un problema combinatorio; consideremos el caso de las desigualdades solamente, y luego el caso mixto.

\(I\)desigualdades, sin igualdades. \(n\)de las desigualdades definirán el vértice de la solución. El número de combinaciones de ecuaciones de\(n\) restricción entre las\(I\) elecciones es\(I!/(I −n)!n!\). Algoritmo: Para cada combinación (indexada\(k\), digamos) a su vez, resolver el sistema lineal de ecuaciones para encontrar una solución\(x_k\). Comprobar que la solución no viole ninguna de las otras restricciones de\(I-n\) desigualdad. De todas las soluciones que son factibles (es decir, no violan ninguna restricción), elige la mejor, es óptima.
\(I\)desigualdades,\(E\) igualdades. La solución involucra todas las igualdades y restricciones de\(n-E\) desigualdad. El número de combinaciones de ecuaciones de\(n-E\) restricción entre las\(I\) elecciones es\(I! / (I-n+E)! (n-E)!\). Algoritmo: Para cada combinación (indexada con\(k\)) a su vez, resolver el conjunto lineal de ecuaciones, para dar una solución candidata\(x_k\). Comprobar que la solución no viole ninguna de las restricciones de\(I-n+E\) desigualdad restantes. De todas las soluciones factibles, elige la mejor, es óptima.

La receta aproximada anterior supone que ninguna de las hipersuperficies es paralela; las restricciones paralelas no se cruzarán y no existe solución al conjunto lineal de ecuaciones. Por suerte tales casos pueden ser detectados fácilmente (por ejemplo, comprobando la singularidad de la matriz), y clasificados como inviables. En la figura anterior,\(I = 5\) y\(n = 2\). De ahí que haya\(5!/(5-2)!2! = 10\) combinaciones a probar: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE. Sólo cinco son evidentes, porque algunas de las intersecciones se encuentran fuera del área señalada (¿Puedes encontrarlas todas?).

El enfoque de programación lineal es extremadamente valioso en muchas áreas de política y finanzas, donde los costos escalan linealmente con la cantidad, y las desigualdades son comunes. También hay muchas aplicaciones de ingeniería, debido a la prevalencia del análisis lineal.