7.5: Programación lineal de enteros

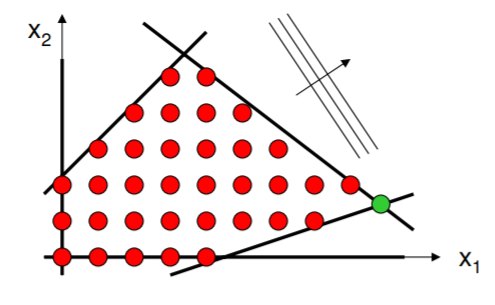
A veces las funciones de restricción y costo son continuas, pero solo se permiten soluciones enteras. Tal es el caso en los mercados de materias primas, donde se espera que se negocien en toneladas de mantequilla, automóviles enteros, y así sucesivamente. La siguiente imagen muestra soluciones enteras dentro de un dominio factible definido por desigualdades continuas de función. Tenga en cuenta que el requisito de una solución entera hace que sea mucho menos obvio cómo seleccionar el punto óptimo; ya no es un vértice.

Figura 7.3.1, donde solo se permiten soluciones a los valores enteros que caen dentro de la región delimitada. La solución identificada en la última sección, marcada en verde, no es un número entero y por lo tanto ya no es una solución aceptable.

El método de ramificación y encuadernación viene al rescate. En palabras, lo que haremos es resolver sucesivamente problemas de programación lineal continua, pero a la vez que impondremos nuevas restricciones de desigualdad que obligan a los elementos a tomar valores enteros.

El método utiliza dos conceptos principales. El primero tiene que ver con límites y es bastante intuitivo. Supongamos que en un dominio de solución\(X_1\), el costo tiene un límite superior conocido\(\bar{f}_1\), y que en un dominio diferente\(X_2\), el costo tiene un límite inferior conocido\(\underline{f}_1\). Supongamos además eso\(\bar{f}_1 < \underline{f}_2\). Si se desea minimizar la función, entonces tal comparación sugiere claramente que no necesitamos pasar más tiempo trabajando en\(X_2\). El segundo concepto es el de un árbol ramificado, y un ejemplo es la mejor manera de proceder aquí. Tratamos de maximizar\(^1\)

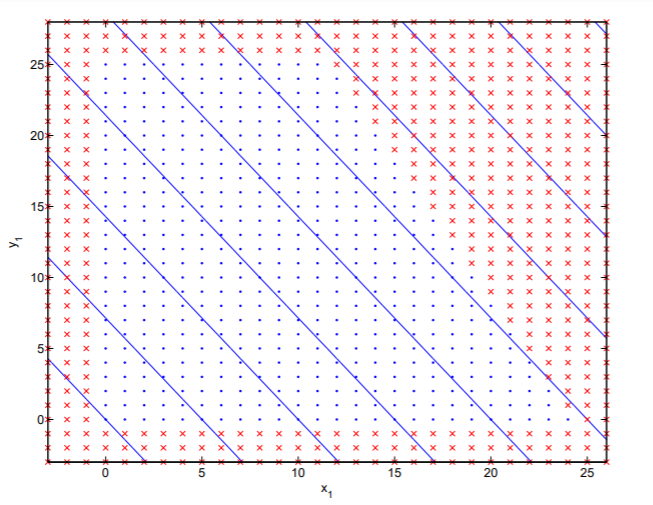
\ begin {alinear*} J\, &=\, 1000 x_1 + 700 x_2,\ textrm {sujeto a}\\ [4pt] 100 x_1 + 50 x_2\, &\ leq\, 2425\ textrm {y}\\ [4pt] x_2\, &\ leq\, 25.5.\ [4pt] &\\ quad\ textrm {con ambos enteros\(x_1, \, x_2\) positivos}\ end {align*}

Figura\(\PageIndex{2}\): el rango de posibles valores enteros para soluciones a este problema, con valores permitidos indicados por puntos azules.

De ahí que tengamos cuatro restricciones de desigualdad; el problema no es diferente a lo que se muestra en la figura anterior. Primero, resolvemos el problema de programación lineal continua, encontrando

\[ A: \, J = 29350 \, : \, x_1 = 11.5, \, x_2 = 25.5 \nonumber \]Claramente, debido a que ninguno de los elementos de la solución es un entero, esta solución no es válida. Pero sí nos da un punto de partida en rama y encuadernado: Ramificar esta solución en dos, donde consideramos los enteros\(x_2\) más cercanos a\(25.5\):

\ begin {alinear*} B:\, J (x_2\ leq 25)\, &=\, 29250\,:\, x_1 = 11.75,\, x_2 = 25\ textrm {y}\\ [4pt] C:\, J (x_2\ geq 26)\, &=\, X,\ end {align*}

donde\(X\) indica que hemos violado una de nuestras limitaciones originales. Entonces no hay nada más que considerar en la línea de\(C\). Pero perseguimos\(B\) porque todavía tiene soluciones no enteras, ramificándose\(x_1\) en

\ begin {alinear*} D:\, J (x_1\ leq 11,\, x_2\ leq 25)\, &=\, 28500\,:\, x_1 = 11, x_2 = 25\ textrm {y}\\ [4pt] E:\, J (x_1\ geq 11,\, x_2\ leq 25)\, &=\, 29150\,:\, x_1 = 12, x_2 = 24.5. \ end {alinear*}

\(D\)no necesita ser perseguido más, ya que es tiene soluciones enteras; almacenamos\(D\) como un posible óptimo. Ampliando\(E\) en\(x_2\), obtenemos

\ begin {alinear*} F:\, J (x_1\ geq 12,\, x_2\ leq 24)\, &=\, 29050\,:\, x_1 = 12.25,\, x_2 = 24,\ textrm {y}\\ [4pt] G:\, J (x_1\ geq 12,\, x_2\ leq 25)\, &=\, X.\ end {align*}

\(G\)es inviable porque viola una de nuestras limitaciones de desigualdad originales, por lo que esta rama muere. \(F\)tiene soluciones no enteras por lo que nos ramificamos en\(x_1\):

\ begin {alinear*} H:\, J (x_1\ leq 12,\, x_2\ leq 24)\, &=\, 28800\,:\, x_1 = 12,\, x_2 = 24\ textrm {y}\\ [4pt] I:\, J (x_1\ geq 13,\, x_2\ leq 24)\, &=\, 28750\,:\, x_1 = 13,\, x_2 = 22.5. \ end {alinear*}

Ahora\(I\) es una solución no entera, pero aun así no es tan buena como\(H\), que sí tiene una solución entera, así que no hay nada más que perseguir\(I\). \(H\)es mejor que\(D\), la otra solución entera disponible - por lo que es la óptima.

Figura\(\PageIndex{3}\): representación visual del razonamiento detrás del método branch-and-bound. Los valores que caen fuera de los límites permitidos se abandonan y se marcan en rojo; los puntos de ramificación viables están en blanco; las soluciones que satisfacen todas las condiciones se marcan en naranja pálido para su posterior comparación, con el azul marcando la óptima entre estas posibles soluciones.

Existen muchos programas comerciales para soluciones ramificadas y enlazadas de problemas de programación lineal entera. Implícitamente usamos el superior-vs. -concepto de límite inferior al terminar en\(I\): si una solución no entera está dominada por cualquier solución entera, ninguna rama de ella puede hacerlo mejor tampoco.

---

\(^{\PageIndex{1}}\): Este problema es de G. Sierksma, Programación lineal y entera, Marcel Dekker, Nueva York, 1996.