7.6: Optimización Mín-Máx para Opciones Discretas

Última actualización
Guardar como PDF

Page ID: 84138

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un dilema común en la optimización es la existencia de múltiples funciones objetivas. Por ejemplo, en la compra de un motor, tenemos potencia nominal, peso, durabilidad y así sucesivamente a considerar. Aunque se tratara de un trabajo personalizado -en cuyo caso las variables pueden variarse continuamente- el hecho de muchos objetivos lo hace desordenado. Los problemas de optimización limpia minimizan una función, pero si hacemos una metafunción a partir de muchas funciones más simples (por ejemplo, una suma ponderada), invariablemente encontramos que la solución es bastante sensible a cómo construimos la meta-función. ¡Esto no es como debería ser! La siguiente figura muestra a la izquierda una compensación típica de objetivos: uno se mejora a expensas de otro. Ambas son funciones de los parámetros subyacentes. Construyendo un meta objetivo a la derecha, hay un hecho un mínimo (trazado en contra\(J_1(x)\), pero su ubicación depende directamente de\(\gamma\).

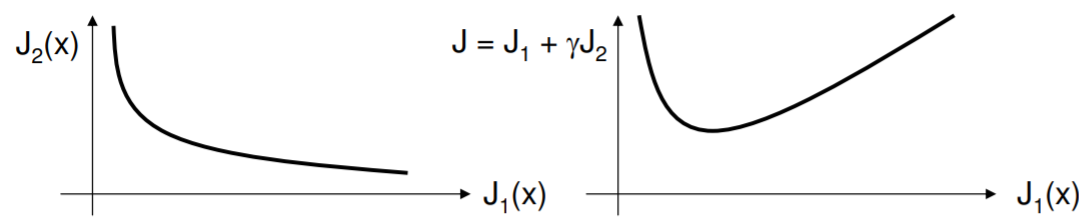Gráfico de una compensación típica entre parámetros (izquierda) contrastada con una metafunción que utiliza una suma ponderada de estos parámetros (derecha). — Figura\(\PageIndex{1}\): las gráficas ilustran la diferencia de comportamiento entre la función de una compensación de dos parámetros objetivos (izquierda), y la metafunción compuesta por la suma ponderada de esos mismos dos parámetros (derecha).

Una muy buena resolución a este problema es el método min-max. Lo que buscamos es la solución candidata con la menor desviación normalizada del rendimiento máximo entre objetivos. Aquí hay un ejemplo que explica. Cuatro candidatos deben ser evaluados de acuerdo a tres métricas de desempeño; mayor es mejor. Tienen puntajes brutos de la siguiente manera:

	Métrico I	Métrico II	Métrico III
Candidato A	\(3.5\)	\(9\)	\(80\)
Candidato B	\(2.6\)	\(10\)	\(90\)
Candidato C	\(4.0\)	\(8.5\)	\(65\)
Candidato D	\(3.2\)	\(7.5\)	\(86\)

Obsérvese que cada métrica es evidentemente dada en diferentes escalas. La Métrica I tal vez se saca de cinco, la Métrica II es de diez quizás, y la Métrica III podría ser de cien. Hacemos cuatro cálculos básicos:

Calcular el rango (max menos el min) para cada métrica: obtenemos\([1.4, 2.5, 35]\).
Escoge la métrica máxima en cada métrica: tenemos\([4.0, 10, 90]\).
Finalmente, reemplace las entradas en la tabla original con la desviación normalizada de la mejor

	Métrico I	Métrico II	Métrico III
Candidato A	\((4.0-3.5)/1.4 = 0.36\)	\((10-9)/2.5 = 0.4\)	\((90-80)/35 = 0.29\)
Candidato B	\((4.0-2.6)/1.4 = 1\)	\((10-10)/2.5 = 0\)	\((90-90)/35 = 0\)
Candidato C	\((4.0-4.0)/1.4 = 0\)	\((10-8.5)/2.5 = 0.6\)	\((90-65)/35 = 1\)
Candidato D	\((4.0-3.2)/1.4 = 0.57\)	\((10-7.5)/2.5 = 1\)	\((90-86)/35 = 0.11\)

Para cada candidato, seleccione la peor desviación (más alta): obtenemos\([0.4, 1, 1, 1]\).

El candidato con lo peor más bajo (¡min del máximo!) la desviación es nuestra elección: Candidato A.

El criterio mínimo-máximo puede romper un log-jam en el caso de múltiples objetivos, pero claro que no está exento de escollos. Por un lado, ¿todas las métricas son igualmente importantes? De no ser así, ¿una suma ponderada de las desviaciones agregaría alguna idea? También notamos que el min-max descartará a un candidato que puntúe en la parte inferior del paquete en cualquier métrica; esto puede o no ser percibido como justo. En términos más amplios, dicha toma de decisiones puede tener aspectos sociales fascinantes.