3.1: Sistemas de coordenadas y marcos de referencia

Todo robot asume una posición en el mundo real que puede describirse por su posición (x, y y z) y orientación (cabeceo, guiñada y balanceo) a lo largo de los tres ejes principales de un sistema de coordenadas cartesianas (Ver también Sección 2.3, “Grados de libertad”).

Figura\(\PageIndex{1}\): Un sistema de coordenadas que indica la dirección de los ejes de coordenadas y la rotación alrededor de ellos. Estas direcciones se han derivado usando las reglas de la derecha.

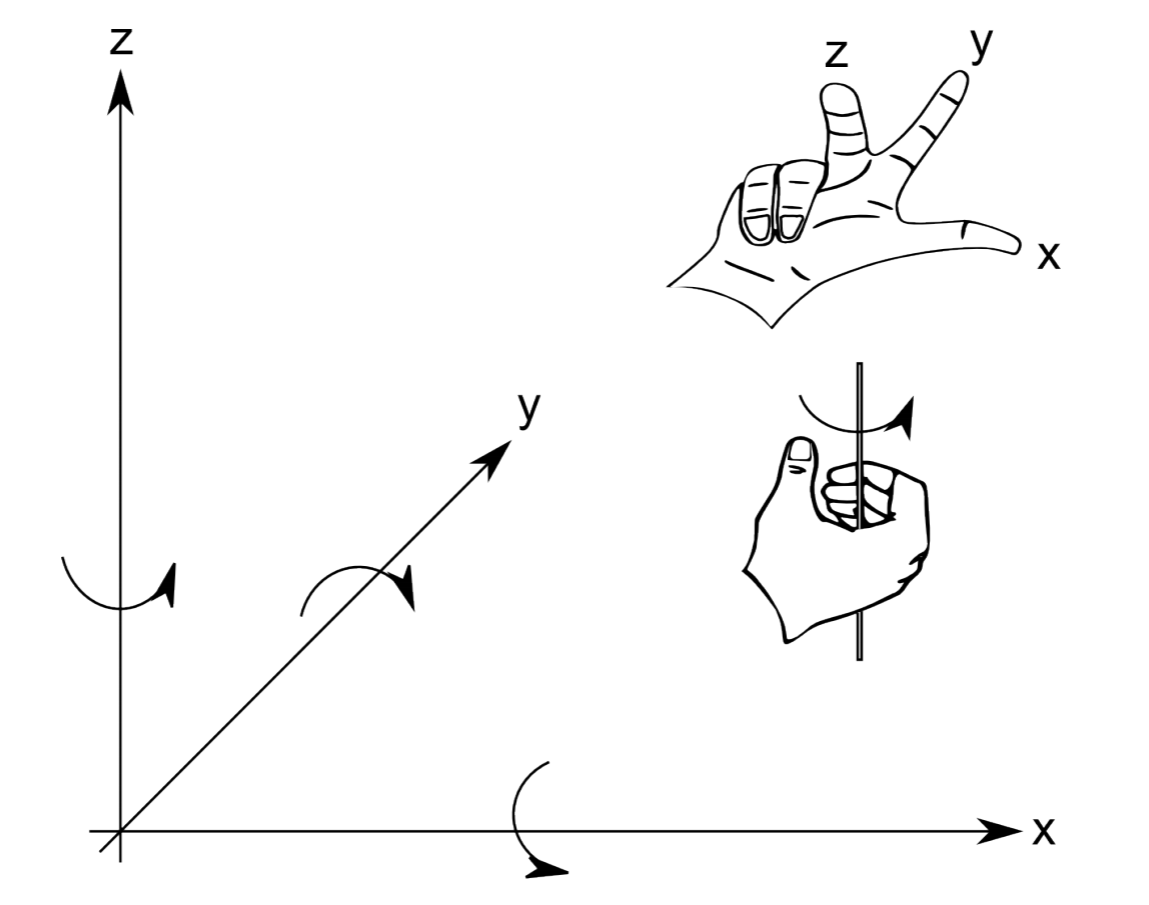
Dicho sistema de coordenadas se muestra en la Figura 3.1.1. Tenga en cuenta que las direcciones y orientaciones de los ejes de coordenadas son arbitrarias. Este libro utiliza las “reglas de la mano derecha”, las cuales se ilustran en la Figura 3.1.1 para determinar las etiquetas de los ejes y las direcciones a lo largo. Pitch, guiñada y roll, también se conocen como banco, actitud y rumbo en otras comunidades. Esto tiene sentido, considerando el uso coloquial de la palabra “rumbo”, que corresponde a una rotación alrededor del eje z de un vehículo que circula en el plano x-y.

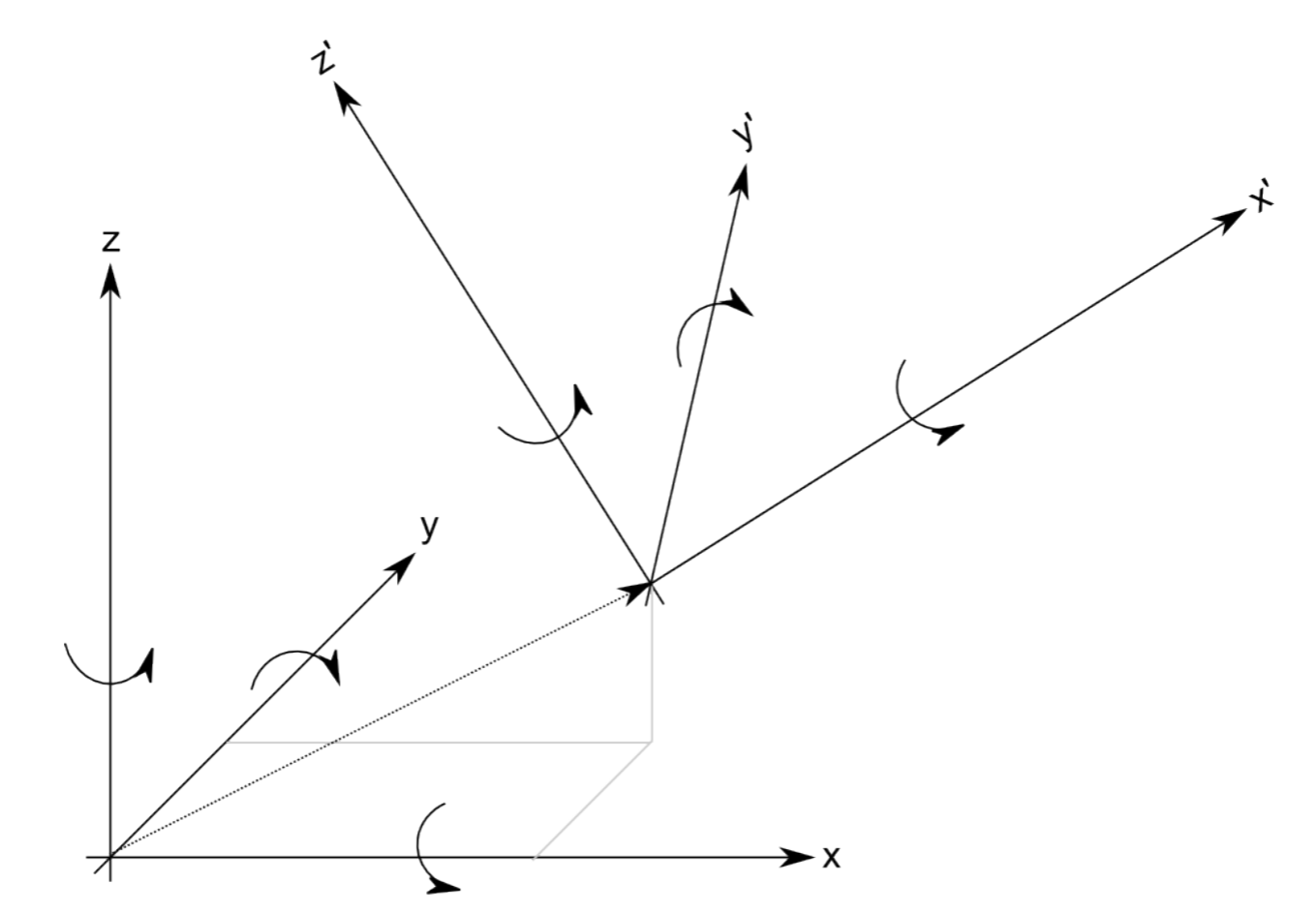
Definir los tres ejes de posición y orientaciones puede ser engorroso. Qué nivel de detalle nos importa, dónde está el origen de este sistema de coordenadas, e incluso qué tipo de sistema de coordenadas elegimos, depende de la aplicación específica. Por ejemplo, un robot móvil simple normalmente requeriría una representación con respecto a una habitación, un edificio o el sistema de coordenadas de la tierra (dado por la longitud y latitud de cada punto de la tierra), mientras que un manipulador estático suele tener el origen de su sistema de coordenadas en su base. Los sistemas más complicados, como los manipuladores móviles o los robots multipatas, hacen la vida mucho más fácil al definir múltiples sistemas de coordenadas, por ejemplo, uno para cada pata y otro que describe la posición del robot en el marco del mundo. Estos sistemas de coordenadas locales se conocen como Marcos de Referencia. Un ejemplo de dos sistemas de coordenadas anidadas se muestra en la Figura 3.1.2. En este ejemplo, un robot ubicado en el origen de x ^', y^' y z ^'podría planificar sus movimientos en su propio marco de referencia, que luego se puede expresar en el sistema de coordenadas x, y y z realizando una traslación y una rotación como veremos más adelante.

Figura\(\PageIndex{2}\): Dos sistemas de coordenadas anidadas (marcos de referencia).

Dependiendo de sus grados de libertad, es decir el número de traslaciones y rotaciones independientes que un robot puede lograr en el espacio cartesiano, también es costumbre ignorar componentes de posición y orientación que permanecen constantes. Por ejemplo, la postura de un simple robot de limpieza de suelos podría estar completamente definida por sus coordenadas x e y en una habitación, así como su orientación, es decir, su rotación alrededor del eje z.

3.1.1. Notación matricial

Dado algún tipo de sistema de coordenadas fijas, podemos describir la posición del efector final de un robot mediante un vector de posición 3x1. Como puede haber muchos sistemas de coordenadas definidos en un robot y en el entorno, identificamos el sistema de coordenadas al que se relaciona un punto mediante un super-script anterior, por ejemplo, ^A P para indicar que el punto P está en el sistema de coordenadas {A}. Cada punto consta de tres elementos ^A P = [p _x p _y p _z] ^T.

Más formalmente, ^A P es una combinación lineal de los tres vectores base que abarcan A:

\ [_ {} ^ {A}\ textrm {P} =p_ {x}\ begin {pmatrix}
1\\
0\
0
\ end {pmatrix} +p_ {y}\ begin {pmatrix}
0\\
1\\
0
\ end {pmatrix} +p_ {z}\ begin {pmatrix}
0\\
0\
1
\ end {pmatrix}\]

Como sabemos, no sólo es importante la posición del robot, sino también su orientación. Para describir la orientación de un punto, le adjuntaremos un sistema de coordenadas. _{Sea X, B y B vectores unitarios que corresponden a los ejes principales de un sistema de coordenadas {B}.} Cuando se expresan en el sistema de coordenadas {A}, se denotan ^A X _B, ^A Y _B y ^A _B. Para expresar un vector que se da en un sistema de coordenadas en otro, necesitamos proyectar cada uno de sus componentes a los vectores unitarios que abarcan el sistema de coordenadas objetivo. Por ejemplo considerando solo el eje ^A X _B

\[_{}^{A}\textrm{}X̂{_{B}}^{}=\left ( X̂{_{B}}^{}.X̂{_{A}}^{}, X̂{_{B}}^{}. Ŷ{_{A}}^{}, X̂{_{B}}^{}.Ẑ{_{A}}^{} \right )^{T}\]

consiste en las proyecciones de X _B sobre X _A, Y _A y _A. Aquí, | · | denota el producto escalar (también conocido como punto o producto interno). Obsérvese que todos los vectores en (3.1.2) son vectores unitarios, es decir, su longitud es uno. Por definición del producto escalar, A · B = ||A|| ||B|| cos α = cos α, efectivamente reduce la proyección de X _B sobre los vectores unitarios de {A}. Esta proyección se ilustra en la Figura 3.1.3.

Figura\(\PageIndex{3}\): Arriba: Un sistema de coordenadas {B} con la posición dada por ^A P y la orientación dada por X _B, Y _B y B. Abajo: La proyección del vector unitario X _B sobre los vectores unitarios que abarcan el sistema de coordenadas {A} después de mover {B} al origen de {A}. Como todos los vectores son vectores unitarios, A · B = ||A|| ||B|| cos α = cos α.

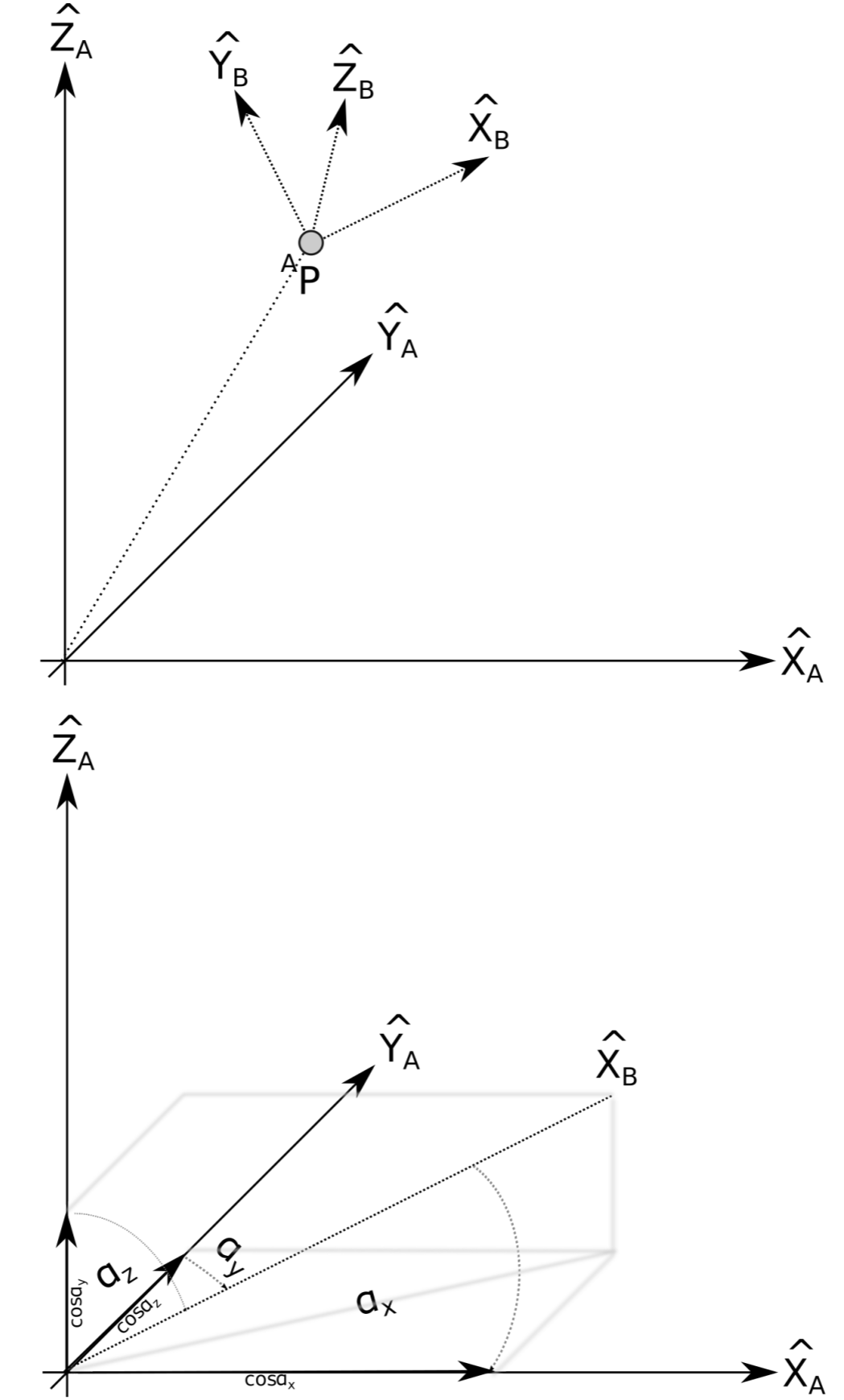
Ahora podemos hacer esto para los tres vectores que abarcan el sistema de coordenadas {B} y apilar estos tres vectores juntos en una matriz 3x3 para obtener la matriz de rotación

\ [_ {B} ^ {A}\ textrm {R} =\ begin {bmatrix}
_ {} _ {} ^ {A} X {_ {B}} ^ {} & _ {} ^ {A} Y {_ {B}} ^ {} & _ {} ^ {A} {_ {B}} ^ {}
\ end {bmatrix}\]

que describe {B} relativo a {A}. Es importante señalar que todas las columnas en _{B ^A} R son vectores unitarios, por lo que la matriz de rotación es ortonormal. Esto es importante ya que esto nos permite obtener fácilmente la inversa de _{B ^A} R como _{B ^A} R ^T o _A ^B R = _{B ^A} R ^T.

Por qué los vectores unitarios de un sistema de coordenadas {B} expresados en el sistema de coordenadas {A} realmente forman una matriz de rotación, se pueden ver fácilmente al reorganizar la Ecuación 3.1.1 en forma de matriz

\ [_ {} ^ {A}\ textrm {P} =\ begin {pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0 & 1
\ end {pmatrix}\ begin {pmatrix}
p_ {x}\\
p_ {y}\\
p_ {z}
\ end {pmatrix}\]

donde la matriz de rotación no es más que la identidad ya que ambos puntos ya están en el mismo sistema de coordenadas.

Ahora hemos establecido cómo expresar la orientación de un sistema de coordenadas utilizando una matriz de rotación. Por lo general, los sistemas de coordenadas no se encuentran uno encima del otro, sino que también se desplazan unos de otros. Juntos, la posición y la orientación se conocen como un marco, que es un conjunto de cuatro vectores, uno para la posición y tres para la orientación, y podemos escribir

\[\left \{ B \right \}=\left \{ _{B}^{A}\textrm{R}, _{}^{A}\textrm{P}\right \}\]

para describir el marco de coordenadas {B} con respecto a {A} usando un vector A P y ^una matriz de rotación _{B ^A} R. Los robots suelen tener muchos de esos marcos definidos a lo largo de sus cuerpos.

3.1.2. Mapeo de un fotograma a otro

Habiendo introducido el concepto de marcos, necesitamos la capacidad de mapear coordenadas en un fotograma a coordenadas en otro marco. Por ejemplo, consideremos que el marco {B} tiene la misma orientación que el marco {A} y sentado en la ubicación ^A P en el espacio. Como la orientación de ambos fotogramas es la misma, podemos expresar un punto ^B Q en el fotograma {A} como

\[_{}^{A}\textrm{Q}=_{}^{B}\textrm{Q}+_{}^{A}\textrm{P}\]

En realidad, sumar dos vectores que están en diferentes marcos de referencia, es decir, ^B Q + ^A P, solo es posible si ambos tienen la misma orientación. Podemos, sin embargo, convertir de un marco de referencia a otro usando la matriz de rotación:

\[_{}^{A}\textrm{P}=_{B}^{A} \textrm{R}^{B}P\]

y por lo tanto resolver el problema de mapeo independientemente de la orientación de {A} a {B}:

\[_{}^{A}\textrm{Q}=_{B}^{A} \textrm{R}^{B}Q+_{}^{A}\textrm{P}\]

Usando esta notación, podemos ver que los subíndices iniciales cancelan los superíndices iniciales de la siguiente matriz vector/rotación. Mientras que ahora tenemos una solución para transferir un punto de un marco de referencia a otro combinando una rotación y una traslación, sería más atractivo escribir algo así:

_ {} ^ {A}\ textrm {Q} =_ {B} ^ {A}\ textrm {T} ^ {B} Q

Para ello, necesitamos introducir un vector de posición 4x1 tal que

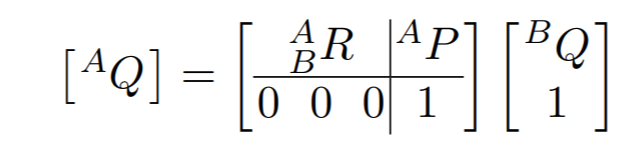
y _{B ^A} T es una matriz 4x4. Tenga en cuenta que los '1's y [0001] agregados no afectan a las otras entradas en la matriz durante la multiplicación de la matriz. Una matriz 4x4 de esta forma se llama transformada homogénea.

La inversa de una transformada homogénea se puede construir invirtiendo la rotación y la parte de traslación de forma independiente, lo que lleva a

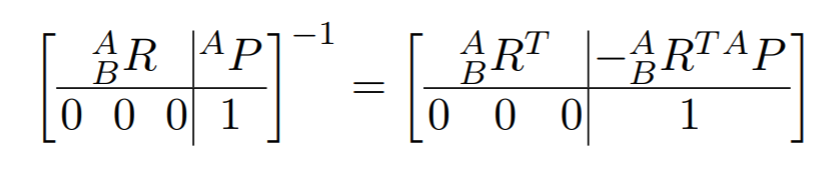
Ahora hemos establecido una notación conveniente para convertir puntos de un sistema de coordenadas a otro. Hay muchas formas posibles de hacer esto, en particular cómo se puede representar la rotación (ver más abajo), pero todas se pueden convertir de una a otra.

3.1.3. Aritmética de transformación

Las transformaciones se pueden combinar: considere por ejemplo un brazo con dos enlaces, un marco de referencia {A} en la base, {B} en su primera articulación y {C} en su efector final. Dadas las transformaciones _C ^B T y _{B ^A} T, podemos escribir

\[_{}^{A}\textrm{P}=_{B}^{A}\textrm{T}_{C}^{B}\textrm{T}_{}^{C}\textrm{P}=_{C}^{A}\textrm{T}_{}^{C}\textrm{P}\]

para convertir un punto en el marco de referencia del efector final al de su base. Como esto funciona para los operadores de rotación y traslación de forma independiente, podemos construir _C ^A T como

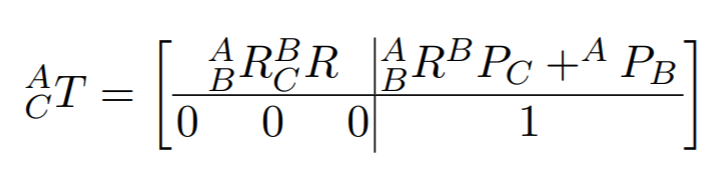
donde ^A P _B y ^B P _C son las traducciones de {A} a {B} y de {B} a {C}, respectivamente.

3.1.4. Otras representaciones para orientación

Hasta el momento, hemos representado la orientación mediante una matriz 3x3 cuyos vectores de columna son vectores unitarios ortogononales que describen la orientación de un sistema de coordenadas. Por lo tanto, la orientación se representa con nueve valores diferentes. Elegimos esta representación principalmente porque es la más intuitiva de explicar y se deriva de la geometría simple.

De hecho, tres valores son suficientes para describir la orientación. Esto queda claro al considerar que la ortogonalidad (el producto punto de todas las columnas es cero) y la longitud del vector (cada vector debe tener longitud 1) imponen seis restricciones sobre los nueve valores en la matriz de rotación. De hecho, una orientación se puede representar alrededor de una rotación por ciertos ángulos alrededor del eje x, y y z del sistema de coordenadas de referencia. Esto se conoce como notación de ángulo fijo X − Y − Z. Matemáticamente, esto puede ser representado por una matriz de rotación de la forma

\ [_ {B} ^ {A}\ textrm {R} _ {XYZ (\ gamma,\ beta,\ alfa)} =\ comenzar {bmatrix}
\ cos\ alfa & -\ sin\ alfa & 0\
\ sin\ alfa &\ cos\ alfa & 0\
0 & 0 & 0 & 1
\ end {bmatrix}\ begin {bmatrix}
\ cos\ beta & 0 &\ sin\ beta\\
0 & 1 & 0\\
-\ sin\ beta & 0 &\ cos\ beta
\ end {bmatrix}\ begin {bmatrix}
1 & 0 & 0 & 0\\
0 &\ cos\ gamma & -\ sin\ gamma\\
0 &\ sin\ gamma &\ cos\ gamma
\ end {bmatrix}\]

Mientras que el enfoque de ángulos fijos X −Y −Z expresa un marco de coordenadas usando rotaciones con respecto al marco de coordenadas original, digamos {A}, otra posible descripción es comenzar con un marco de coordenadas {B} que sea coincidente con el marco {A}, luego rotar alrededor del eje Z con ángulo α, luego el eje Y con ángulo β y finalmente alrededor del eje X con ángulo γ. Esta representación se llama ángulos Z-Y-X Euler. Como el eje de coordenadas no necesariamente tiene que ser diferente, hay doce posibles combinaciones válidas de rotaciones subsecuentes:

XYX, XZX, YXY, YZY, ZXZ, ZYZ, XYZ, XZY, YZX, YXZ, ZXY y ZYX

Solo hay doce, ya que las rotaciones subsecuentes alrededor del mismo eje no son válidas. Dichas rotaciones no agregarían ninguna información, sino que equivalen a una rotación por la suma de ambos ángulos.

Es importante conocer las sutiles diferencias entre las diferentes transformaciones disponibles ya que no hay “correcto” o “incorrecto”, pero diferentes fabricantes y campos utilizan diferentes convenciones. Solo hay una advertencia: cada una de las matrices de rotación puede parecer rotaciones posteriores alrededor del mismo eje para ciertos valores de ángulos. Por ejemplo, esto sucede para la matriz de rotación XYZ si el ángulo de rotación alrededor del eje Y es de 90°. Estos casos se conocen como una singularidad.

Entre estos, la representación preferida por razones computacionales y de estabilidad son los Cuaterniones. Un cuaternión es una 4-tupla que extiende los números complejos con aplicaciones muy generales en matemáticas y que representa la orientación y rotación en particular. La idea básica es que cada rotación puede representarse como una rotación alrededor de un solo eje (un vector en el espacio) por un ángulo específico. Dado tal eje K = [k _x k _y k _z] T y un ángulo θ, se pueden calcular los llamados parámetros de Euler o cuaternión unitario:

\[\epsilon _{1}=k_{x}sin\frac{\theta }{2}\]

\[\epsilon _{2}=k_{y}sin\frac{\theta }{2}\]

\[\epsilon _{3}=k_{z}sin\frac{\theta }{2}\]

\[\epsilon _{4}=coz\frac{\theta }{2}\]

Estas cuatro cantidades están restringidas por la relación

\[\epsilon _{1}^{2}+\epsilon _{2}^{2}+\epsilon _{3}^{2}+\epsilon _{4}^{2}=1\]

que podría ser visualizado por un punto en una hiperesfera unitaria. Análogamente a las matrices de rotación, dos cuaterniones _i y '_i se pueden multiplicar usando la siguiente ecuación

\ [\ begin {pmatrix}
\ épsilon _ {4} &\ épsilon _ {1} &\ épsilon _ {2} &\ épsilon _ {3}\\
-\ épsilon _ {1} &\ épsilon _ {4} & -\ épsilon _ {3} &\ épsilon _ {2} &\ épsilon _ {2} &\ épsilon _ {3} &\ épsilon _ {4} & -\ épsilon _ {1} ^ {c}\\

-\ épsilon _ {3} & -\ épsilon _ {2} &\ épsilon _ {1} &\ épsilon _ {4}
\ end {pmatrix}\ begin {pmatrix}
\ epsilon _ {4} ^ {'}\\ épsilon _ {1} ^ {'}
\\ épsilon _ {2} ^ {'}
\\ epsilon _ {2} ^ {'}
\\ épsilon on _ {3} ^ {'}
\ end {pmatrix}\]

A diferencia de multiplicar dos matrices de rotación, que requiere 27 multiplicaciones y 18 adiciones, multiplicar dos cuaterniones solo requiere 16 multiplicaciones y 12 adiciones, haciendo la operación computacionalmente más eficiente. Además, la representación cuaternión no sufre de singularidades para ángulos de articulación específicos, haciendo que el enfoque computacionalmente sea más robusto.

Por qué cualquier rotación puede ser expresada por un solo vector se puede ver al considerar las propiedades de las matrices de rotación ortonómica. Tienen tres Autovalores λ = 1 y un par complejo λ1,2 = cos θ ± i sin θ. Los valores propios y los vectores propios se definen como Rv = λv. Para el caso de λ = 1, el correspondiente Eigenvector v no se modifica por rotación. Esto solo es posible si v es el eje de rotación real. El ángulo de rotación ahora viene dado por θ, que se puede inferir del par complejo.