3.2: Cinemática hacia delante de Mecanismos seleccionados

Ahora que hemos introducido la noción de marcos de coordenadas locales, nos interesa cómo calcular la pose y la velocidad de estos marcos de coordenadas en función de los actuadores del robot. Primero consideraremos mecanismos simples donde podemos determinar la relación entre los actuadores y la pose de varios cuadros en el robot tanto en el dominio de posición como de velocidad. Luego consideraremos la clase especial de mecanismos no holonómicos utilizando una serie de robots con ruedas, para lo cual la cinemática de avance solo puede calcularse en el dominio de la velocidad.

3.2.1. Cinemática delantera de un brazo simple

Figura\(\PageIndex{1}\): Un brazo simple de 2 DOF.

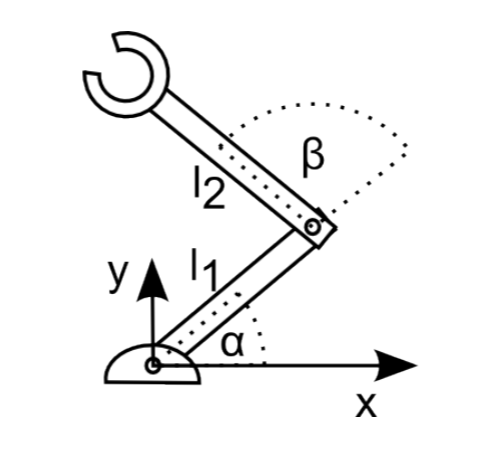
Considera un brazo de robot hecho de dos eslabones y dos articulaciones que se monta en una mesa. Que la longitud del primer enlace sea l ₁ y la longitud del segundo enlace sea l ₂. Se podría especificar la posición del enlace más cerca de la tabla por el ángulo α y el ángulo del segundo enlace relativo al primer enlace usando el ángulo β. Las convenciones adecuadas y los sistemas de coordenadas se muestran en la Figura 3.2.1.

Ahora podemos calcular la posición de la articulación entre el primer y el segundo enlace usando trigonometría simple:

\[x_{1}=\cos\alpha l_{1}\]

\[y_{1}=\sin\alpha l_{1}\]

De manera similar, la posición del efector final viene dada por

\[x_{2}=\cos(\alpha +\beta )l_{2}+x_{1}\]

\[y_{2}=\sin(\alpha +\beta )l_{2}+y_{1}\]

o juntos, la posición del efector final (x, y) viene dada por

\[x=\cos(\alpha +\beta)l_{2}+\cos\alpha l_{1}\]

\[y=\sin(\alpha +\beta)l_{2}+\sin\alpha l_{1}\]

Las ecuaciones anteriores son las ecuaciones cinemáticas de este robot ya que relacionan sus parámetros de control α y β con la posición de su efector final dada en el sistema de coordenadas local abarcado por x e y con el origen en la base del robot. Obsérvese que tanto α como β mostrados en la figura son positivos: Ambos enlaces giran alrededor del eje z. Usando la regla de la derecha, la dirección de los ángulos positivos se define para ser antihorario.

El espacio de configuración, es decir, el conjunto de ángulos en los que se puede establecer cada actuador, de este robot viene dado por −π/2 < α < π/2 ya que no se supone que se encuentre con la tabla, y −π < β < π. El espacio de configuración se da con respecto a las articulaciones del robot y nos permite calcular el espacio de trabajo del robot, es decir, el espacio físico al que se puede mover, utilizando las ecuaciones cinemáticas hacia adelante. Esta terminología será idéntica para los robots móviles. En la Figura 3.2.2 se muestra un ejemplo de configuración y espacio de trabajo tanto para un manipulador como para un robot móvil.

La orientación del efector final del brazo viene dada por α+β. Ahora podemos escribir una transformación que incluya una rotación alrededor del eje z

\ [\ begin {pmatrix}
cos_ {\ alpha\ beta} &-sin_ {\ alpha\ beta} & 0 &\ cos_ {\ alpha\ beta} l_ {2} +\ cos\ alpha l_ {1}\\
sin_ {\ alpha\ beta} & cos_ {\ alpha\ beta} & 0 &\ sin_ {\ alpha\ beta} l_ {2} +\ sin alfa\ l_ {1}\\
0 & 0 & 1 & 0\\
0& 0 & 0 & 1
\ end {pmatrix}\]

La notación sinαβ y cosαβ son de mano corta para sin (α + β) y cos (α + β), respectivamente.

Esta transformación ahora nos permite traducir de la base del robot al efector final del robot en función de las posiciones α y β del actuador. Esta transformación será útil si queremos calcular ángulos de articulación adecuados para alcanzar una determinada pose o si queremos convertir las medidas tomadas en relación con el efector final de nuevo en el sistema de coordenadas de la base.

3.2.2. Cinemática delantera de un robot de ruedas diferenciales

Mientras que la postura de un manipulador robótico se define de manera única por sus ángulos de articulación, que pueden estar disponibles usando codificadores casi en tiempo real, este no es el caso de un robot móvil. Aquí, los valores del codificador simplemente se refieren a la orientación de las ruedas y necesitan integrarse a lo largo del tiempo, lo que será una enorme fuente de incertidumbre como veremos más adelante. Lo que complica la materia es que para los llamados sistemas no holonómicos, no basta con medir simplemente la distancia que recorrió cada rueda, sino también cuando se ejecutó cada movimiento.

Figura\(\PageIndex{2}\): Espacio de configuración (izquierda) y espacio de trabajo (derecha) para un robot móvil no holonómico (arriba) y un manipulador holonómico (abajo). Las trayectorias cerradas en el espacio de configuración dan como resultado trayectorias cerradas en el espacio de trabajo si la cinemática del robot es holonómica.

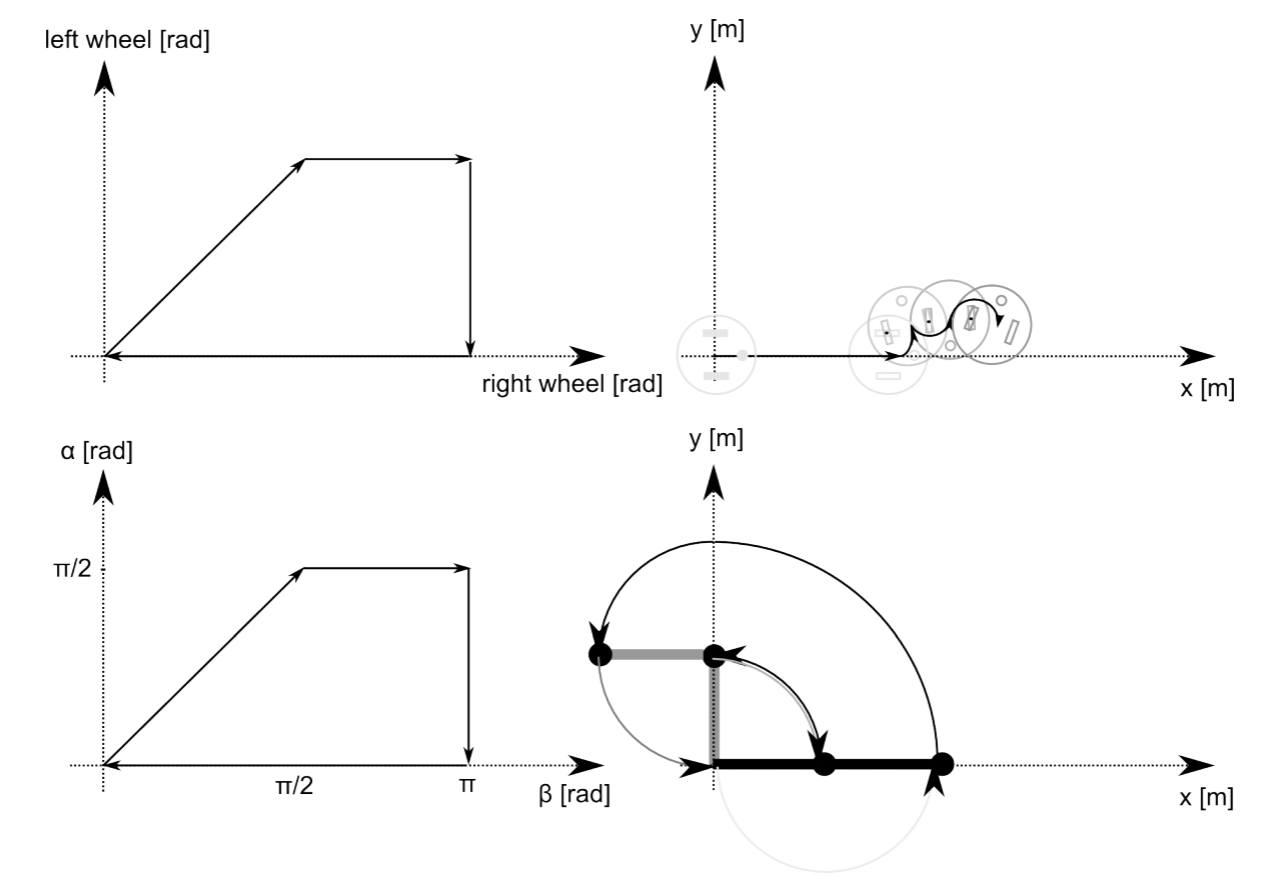
Un sistema no es holonómico cuando las trayectorias cerradas en su espacio de configuración (recordatorio: el espacio de configuración de un brazo robótico de dos eslabones se extiende por los posibles valores de cada ángulo) puede no hacer que vuelva a su estado original. Un brazo simple es holonómico, ya que cada posición articular corresponde a una posición única en el espacio. Pasando por cualquier trayectoria que regrese al punto de partida en el espacio de configuración, colocará al robot exactamente en la misma posición. Un tren en una vía es holonómico: mover sus ruedas hacia atrás en la misma cantidad que han estado avanzando lleva al tren a la misma posición exacta en el espacio. Un automóvil y un robot de rueda diferencial son vehículos no holonómicos: realizar una línea recta y luego un giro a la derecha conduce a la misma cantidad de rotación de rueda que hacer un giro a la derecha primero y luego ir en línea recta; llevar el robot a su posición inicial requiere no solo rebobinar ambas ruedas por el misma cantidad, pero también consiguiendo sus velocidades relativas correctas. La configuración y trayectorias de espacio de trabajo correspondientes para un robot no holonómico y un robot holonómico se muestran en la Figura 3.2.2. Aquí, un robot primero se mueve en línea recta (ambas ruedas giran una cantidad igual). Entonces la rueda izquierda permanece fija y solo la rueda derecha gira hacia adelante. Entonces la rueda derecha permanece fija y la rueda izquierda gira hacia atrás. Finalmente, la rueda derecha gira hacia atrás, llegando a los valores iniciales del codificador (cero). Sin embargo, el robot no vuelve a su origen. Al realizar una trayectoria similar en el espacio de configuración de un manipulador de dos eslabones, en su lugar, dejar que el robot regrese a su posición inicial.

Ya debería quedar claro que para un robot móvil, no sólo importa la distancia recorrida por rueda, sino también la velocidad de cada rueda en función del tiempo. En cambio, esta información no fue necesaria para determinar de manera única la postura de un brazo manipulador. Vamos a introducir las siguientes convenciones. Estableceremos un sistema de coordenadas mundiales {I}, que se conoce como el marco inercial por convención (Figura 3.6). Establecemos un sistema de coordenadas {R} en el robot y expresamos la velocidad ^R del robot como vector

\[_{}^{R}\textrm{ξ} =\left [ _{}^{R}\textrm{x}, _{}^{R}\textrm{y},_{}^{R}\textrm{θ}\right ]^{T}\nonumber\]

Aquí R _x y R _y corresponden a la velocidad a lo largo de las direcciones x e y en {R}, mientras que R _θ corresponde a la rotación alrededor del eje z imaginario, que puedes imaginar que sobresale del suelo. Denotamos velocidades con puntos sobre el nombre de la variable, ya que la velocidad es simplemente la derivada de la distancia. Piensa en la posición del robot en {R}. Siempre es cero, ya que el sistema de coordenadas se fija en el robot. Por lo tanto, las velocidades son las únicas cantidades interesantes en este sistema de coordenadas y necesitamos entender cómo las velocidades en {R} mapean a posiciones en {I}, que denotamos por ^I = [^I x, ^I y, ^I θ] ^T. Estos sistemas de coordenadas se muestran en la Figura 3.2.3.

Figura\(\PageIndex{3}\): Robot móvil con sistema de coordenadas locales {R} y marco mundial {I}. Las flechas indican la dirección positiva de los vectores de posición y orientación.

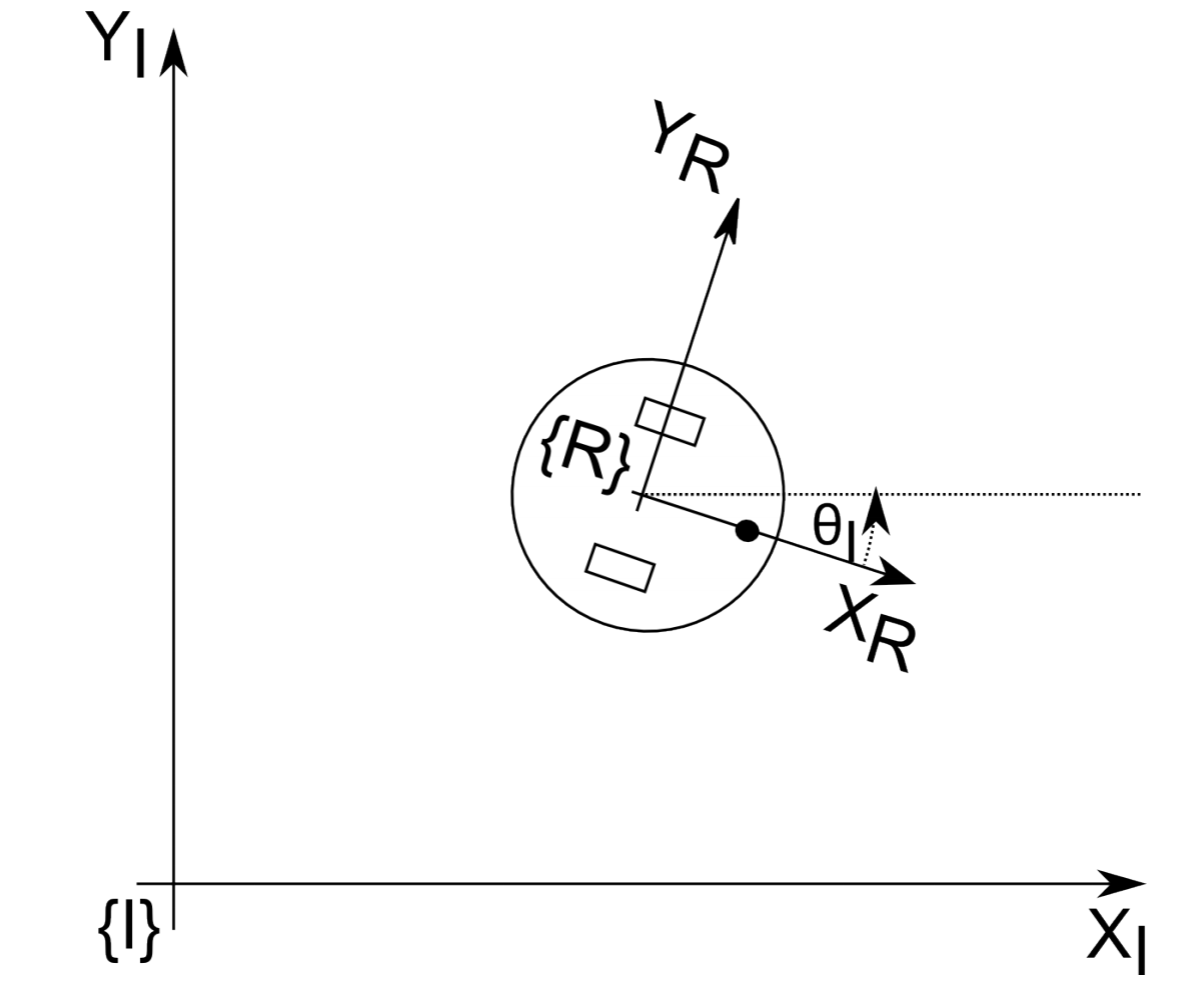
Observe que el posicionamiento de los marcos de coordenadas y su orientación son arbitrarios. Aquí, elegimos colocar el sistema de coordenadas en el centro del eje del robot y alinear ^R x con su dirección de conducción predeterminada.

Para calcular la posición del robot en el marco inercial, primero debemos averiguar cómo la velocidad en el marco de coordenadas del robot se mapea con la velocidad en el marco inercial. Esto se puede hacer de nuevo empleando trigonometría. Solo hay una complicación: un movimiento hacia el eje x del robot podría conducir a un movimiento a lo largo tanto del eje x como del eje y del marco de coordenadas mundiales. Al observar la figura anterior, podemos derivar los siguientes componentes a x _I. En primer lugar,

\[x_{I,x}=cos(\theta)x_{R}\]

También hay un componente de movimiento proveniente de y _R (ignorando las restricciones cinemáticas por ahora, ver más abajo). Para θ negativo, como en la Figura 3.2.3, un movimiento a lo largo de y _R permitiría al robot moverse en dirección X _I positiva. Por lo tanto, la proyección desde yr viene dada por

\[x_{I,y}=-sin(\theta)y_{R}\]

Ya podemos escribir

\[x_{I,y}=cos(\theta)x_{R}-sin(\theta)y_{R}\]

Razonamiento similar lleva a

\[y_{I}=sin(\theta)x_{R}+cos(\theta)y_{R}\]

y

\[\theta _{I}=\theta _{R}\]

que es el caso porque tanto el robot como el sistema de coordenadas mundiales comparten el mismo eje z en este ejemplo. Ahora podemos escribir convenientemente

\[\xi _{I}=_{R}^{I}\textrm{T}(\theta )\xi _{R}\]

con

\ [_ {R} ^ {I}\ textrm {T} (\ theta) =\ begin {pmatrix}
cos (\ theta) & -sin (\ theta) & 0\\
sin (\ theta) & cos (\ theta) & 0\\
0& 0 & 1
\ end {pmatrix}\]

Ahora nos quedamos con el problema de cómo calcular la velocidad _R en las coordenadas del robot. Para ello, hacemos uso de las restricciones cinemáticas de las ruedas robóticas. Para una rueda estándar, las restricciones cinemáticas son que cada rotación de la rueda conduce a un movimiento estrictamente hacia adelante o hacia atrás y no permite el movimiento lateral o el deslizamiento. Por lo tanto, podemos calcular la velocidad de avance de una rueda x usando su velocidad de rotación φ (suponiendo que el valor/ángulo del codificador se expresa como φ) y el radio r por

\[x=\phi r\]

Esto se hace evidente al considerar que la circunferencia de una rueda con radio r es 2πr. La distancia que rueda una rueda cuando gira por el ángulo φ (en radianes) es por lo tanto x = φr, ver también Figura 3.2.4, derecha. Tomando la derivada de esta expresión en ambos lados conduce a la expresión anterior.

Figura\(\PageIndex{4}\): Izquierda: Robot de rueda diferencial pivotando alrededor de su rueda izquierda. Derecha: Una rueda con radio r se mueve por φr cuando gira φ grados.

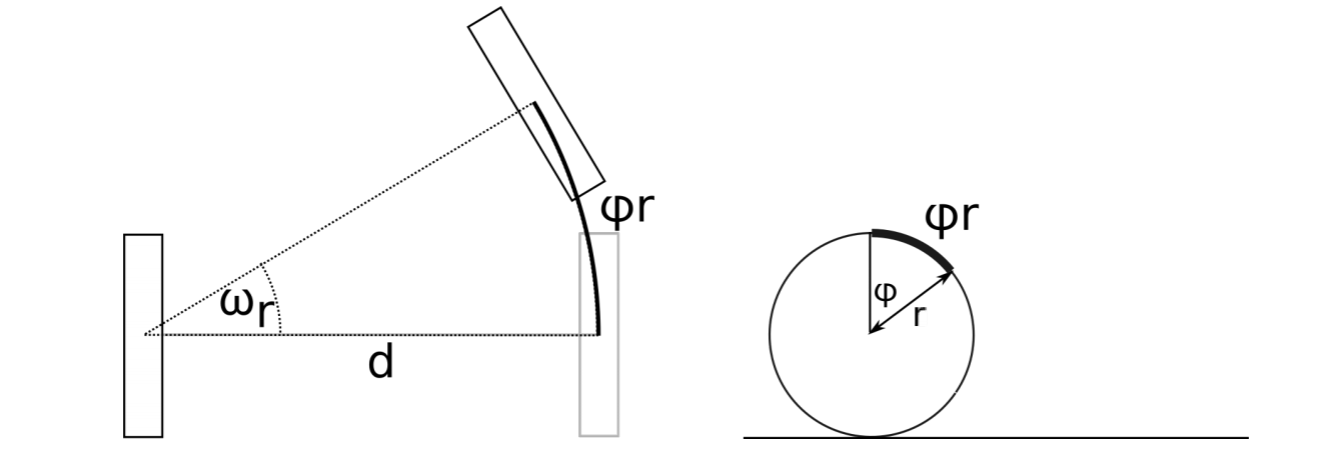
Cómo cada una de las dos ruedas de nuestro ejemplo contribuye a la velocidad del centro del robot, donde está anclado su sistema de coordenadas, requiere el siguiente truco: calculamos la contribución de cada rueda individual mientras asumimos que todas las demás ruedas permanecen sin accionar. En este ejemplo, la distancia recorrida por el punto central es exactamente la mitad de la recorrida por cada rueda individual, asumiendo que la rueda no accionada gira alrededor de su punto de contacto con el suelo (Figura 3.2.4). Por lo tanto, podemos escribir

\[x_{R}=\frac{r\phi _{l}}{2}+\frac{r\phi _{r}}{2}\]

dadas las velocidades φ _l y φ _r de la rueda izquierda y derecha, respectivamente.

Nota

Piense en cómo la velocidad del robot a lo largo de su eje y se ve afectada por la velocidad de la rueda dado el sistema de coordenadas en el dibujo anterior. Piense en las restricciones cinemáticas que imponen las ruedas estándar.

Difícil de creer al principio, pero la velocidad del robot a lo largo de su eje y siempre es cero. Esto se debe a que las limitaciones de la rueda estándar nos dicen que el robot nunca puede deslizarse. Ahora nos queda calcular la rotación del robot alrededor de su zaxis. Que existe tal cosa se puede ver de inmediato al tomar imágenes de las ruedas del robot girando en direcciones opuestas. Nuevamente consideraremos cada rueda de forma independiente. Suponiendo que la rueda izquierda no esté accionada, hacer girar la rueda derecha hacia adelante conducirá a una rotación en sentido antihorario. Dado un diámetro de eje (distancia entre las ruedas del robot) d, ahora podemos escribir

\[\omega_{r}d=\phi_{r}r\]

con ω _r el ángulo de rotación alrededor de la rueda izquierda (Figura 3.2.4, derecha). Tomando la derivada en ambos lados produce velocidades y podemos escribir

\[\omega_{r}=\frac{\phi_{r}r}{d} \]

Agregar las velocidades de rotación (con la que está alrededor de la rueda derecha es negativa según la regla de agarre de la derecha), conduce a

\[\omega_{r}=\frac{\phi_{r}r}{d}-\frac{\phi_{l}r}{d} \]

Poniéndolo todo junto, podemos escribir

\ [\ begin {pmatrix}
x_ {I}\\
y_ {I}\\
\ theta
\ end {pmatrix} =\ begin {pmatrix}
cos (\ theta) & -sin (\ theta) & 0\\
sin (\ theta) & cos (\ theta) & 0\\ 0
&0 &0 &1
\ end {pmatrix}\ begin {pmatrix}
\ frac {r\ phi _ {l}} {2} +\ frac {r\ phi _ {r}} {2}\\
0\
\ frac {\ phi _ {r} r} {d} -\ frac {\ phi _ {l} r} {d}
\ end {pmatrix}\]

De la Cinemática Avanzada a la Odometría

La ecuación 3.2.20 solo nos proporciona la relación entre la velocidad de rueda del robot y su velocidad en el marco inercial. El cálculo de su pose real en el marco inercial se conoce como odometría. Técnicamente, requiere integrar (3.2.20) de 0 a la hora actual T. Como esto no es posible, pero para casos muy especiales, se puede aproximar la pose del robot sumando velocidades en intervalos de tiempo discretos, o más precisamente

\ [\ begin {pmatrix}
x_ {I} (T)\\
y_ {I} (T)\\
\ theta (T)
\ end {pmatrix} =\ int_ {0} ^ {T}\ begin {pmatrix}
x_ {I} (t)\\
y_ {I} (t)\\ theta (t)
\\ theta (t)
\ end {pmatrix} dt\ approx\ suma _ {k=0} ^ {k=T}\ comenzar {pmatrix}
\ Delta x_ {I} (k)\\
\ Delta y_ {I} (k)\\
\ Delta\ theta (k)
\ final {pmatrix}\ Delta t\]

que puede calcularse incrementalmente como

\[x_{I}(k+1)=x_{I}(k)+\Delta x(k)\]

usando ∆x (k) ≈ x _I (t) y expresiones similares para y _I y θ. Tenga en cuenta que (3.2.22) es solo una aproximación. Cuanto más grande se vuelve ∆t, más inexacta se vuelve esta aproximación, ya que la velocidad del robot podría cambiar durante el intervalo.

Nota

¡No dejes que te preocupe la noción de integral! Como las computadoras de los robots son fundamentalmente discretas, las integrales generalmente se convierten en sumas, que no son más que bucles for.

3.2.3. Cinemática delantera de la dirección similar a un automóvil

Las ruedas diferenciales son muy populares en la robótica móvil, ya que son muy fáciles de construir, mantener y controlar. Aunque no holonómico, un accionamiento diferencial puede aproximarse a la función de un robot completamente holonómico conduciendo primero en el lugar para lograr el rumbo deseado y luego conducir recto. Los inconvenientes del accionamiento diferencial son su dependencia de una rueda giratoria, que funciona mal a altas velocidades, y dificultades para conducir líneas rectas ya que esto requiere que ambos motores conduzcan exactamente a la misma velocidad.

Estos inconvenientes son mitigados por mecanismos similares a automóviles, los cuales son accionados por un solo motor y pueden dirigir sus ruedas delanteras. Este mecanismo se conoce como “dirección Ackermann”. La dirección Ackermann no debe confundirse con la dirección de “plataforma giratoria” donde las ruedas delanteras se fijan en un eje con punto de pivote central. En cambio, cada rueda tiene su propio punto de pivote y el sistema está restringido de tal manera que todas las ruedas del automóvil conducen en círculos con un punto central común, evitando el deslizamiento. Como el mecanismo Ackermann permite que todas las ruedas circulen en círculos con un punto central común, su cinemática se puede aproximar por las de un triciclo con tracción trasera, o incluso más simple por una bicicleta. Esto se muestra en la Figura 3.2.5.

Figura\(\PageIndex{5}\): Izquierda: Cinemática de la dirección tipo automóvil y el modelo de bicicleta equivalente. Derecha: Mecanismo de un vehículo Ackermann.

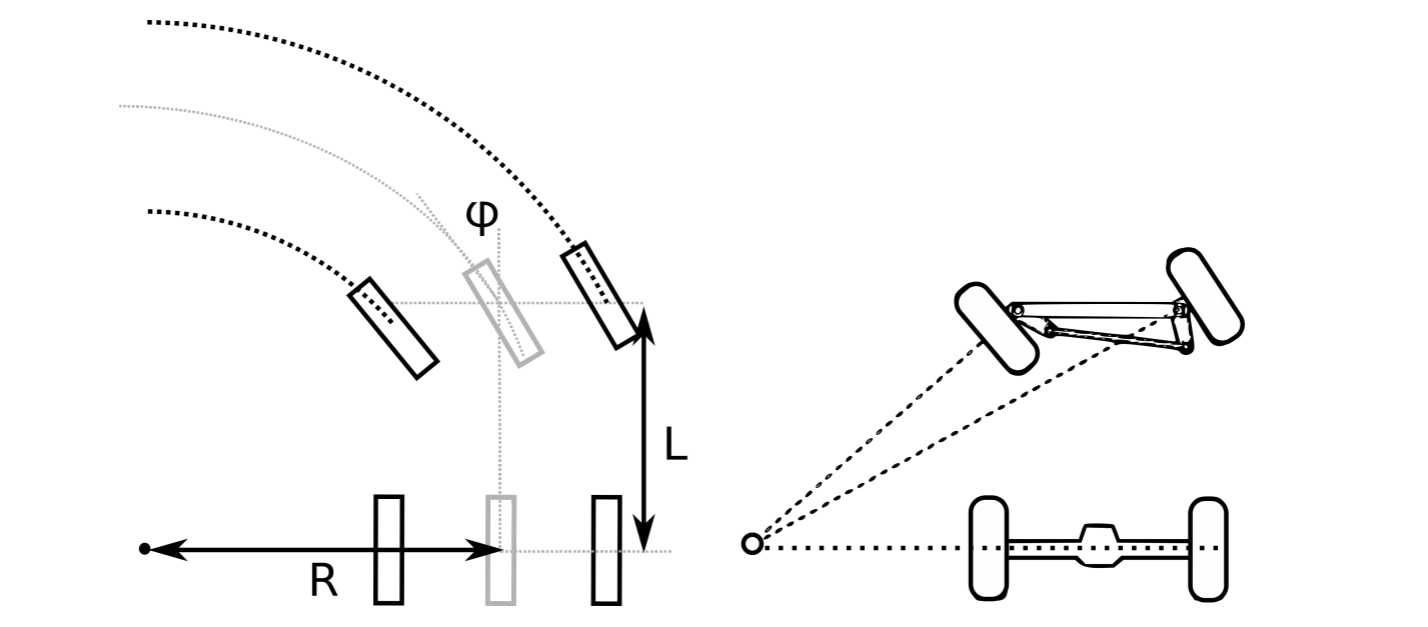
Deja que el carro tenga la forma de una caja con longitud L entre los ejes trasero y delantero. Deje que el punto central del círculo común descrito por todas las ruedas esté a la distancia R de la línea central longitudinal del automóvil. Luego, el ángulo φ de dirección viene dado por

\[\tan\phi =\frac{L}{R}\]

Los ángulos de la rueda izquierda y derecha, φ _l y φ _r se pueden calcular utilizando el hecho de que todas las ruedas del automóvil giran alrededor de círculos con un punto central común. Con la distancia entre las dos ruedas delanteras l, podemos escribir

\[\frac{L}{R-l/2}=\tan(\pi /2-\phi _{r})\]

\[\frac{L}{R+l/2}=\tan(\pi /2-\phi _{l})\]

Esto es importante, ya que nos permite calcular los ángulos de rueda resultantes de un ángulo específico φ y probar si están dentro de las limitaciones del vehículo real. Suponiendo que la velocidad de la rueda sea ω y el radio de rueda r, podemos calcular las velocidades en el marco de coordenadas del robot para

\[x_{r}=\omega _{r}\]

\[y_{r}=0\]

\[\theta _{r}=\frac{\omega r\tan\phi }{L}\]

utilizando (3.2.23) para calcular el radio del círculo R.