3.4: Cinemática inversa de mecanismos seleccionados
- Page ID
- 84886
La cinemática hacia adelante de un sistema viene dada por una matriz de transformación desde la base de un manipulador (o una esquina de la habitación) hasta el efector final de un manipulador (o un robot móvil). Como tales, son una descripción exacta de la pose del robot. Para encontrar los ángulos de articulación que conducen a la pose deseada, necesitaremos resolver estas ecuaciones para los ángulos de articulación en función de la pose deseada. Para un robot móvil, podemos hacer esto solo para velocidades en el sistema de coordenadas local, y necesitamos métodos más sofisticados para calcular trayectorias apropiadas para el robot.
3.4.1. Solvabilidad
Como las ecuaciones resultantes son fuertemente no lineales, tiene sentido pensar brevemente si podemos resolverlas en absoluto para parámetros específicos antes de intentarlo. Aquí, el espacio de trabajo de un robot se vuelve importante. El espacio de trabajo es el subespacio al que puede llegar el robot en cualquier orientación. Claramente, no habrá soluciones para el problema cinemático inverso fuera del espacio de trabajo del robot.
Una segunda pregunta que hacer es cuántas soluciones realmente esperamos y qué significa tener múltiples soluciones geométricamente. Múltiples soluciones para lograr una pose deseada corresponden a múltiples formas en las que un robot puede alcanzar un objetivo. Por ejemplo un brazo de tres eslabones que quiere llegar a un punto al que se puede llegar sin extender completamente todos los eslabones (conduciendo a una sola solución), puede hacer esto doblando sus eslabones de manera cóncava y convexa. Cuántas soluciones hay para un mecanismo dado y pose rápidamente se vuelve poco intuitivo. Por ejemplo, un brazo de 6 DOF puede alcanzar ciertos puntos con hasta 16 conformaciones diferentes.
3.4.2. Cinemática inversa de un brazo manipulador simple
Ahora veremos la cinemática de un brazo de 2 eslabones que presentamos anteriormente. Necesitamos resolver las ecuaciones que determinan la cinemática hacia adelante del robot resolviendo para α y β. Esto es complicado, sin embargo, ya que tenemos que lidiar con expresiones trigonométricas complicadas.
Para obtener una intuición, supongamos que solo hay un enlace, l1. Resolver (3.2.1) para α produce en realidad dos soluciones [cos −1 x1/l1, − cos −1 x1/l1], ya que el coseno es simétrico para valores positivos y negativos. De hecho, para cualquier posición posible en el eje x que va de −l1 a l1, existen dos soluciones. Uno con el brazo encima de la mesa, otro con el brazo dentro de la mesa. (En los extremos del espacio de trabajo, ambas soluciones son las mismas.)
Resolver para ambos grados de libertad en realidad arroja ocho soluciones, de las cuales solo dos son factibles:
\[\alpha \rightarrow \cos^{-1}\left ( \frac{x^{2}y+y^{3}-\sqrt{4x^{4}-x^{6}+4x^{2}y^{2}-2x^{4}y^{2}-x^{2}y^{4}}}{2(x^{2}+y^{2})} \right )\]
y
\[\beta \rightarrow -\cos^{-1}(1/2(-2)x^{2}+y^{2}))\]
Lo que simplificará drásticamente este problema, es no solo especificar la posición deseada, sino también la orientación del efector final. En este caso, una pose deseada puede ser especificada por
\ [\ begin {pmatrix}
cos\ phi & -sin\ phi & 0 & x\
sin\ phi & cos\ phi & 0 &y\\ 0 &
0 & 0 & 1 & 0\\ 0 &
0 & 0 & 0 & 0 & 1
\ end {pmatrix}\]
Ahora se puede encontrar una solución simplemente equiparando las entradas individuales de la transformación (3.2.7) con las de la pose deseada. En concreto, podemos observar
\[cos\phi =cos(\alpha +\beta )\]
\[x=\cos_{\alpha \beta }l_{2}+\cos_{\alpha}l_{1}\nonumber\]
\[y=\sin_{\alpha \beta }l_{2}+\sin_{\alpha}l_{1}\nonumber\]
Estos se pueden reducir a
\ phi =\ alfa +\ beta
\[\cos\alpha =\frac{\cos_{\alpha \beta }l_{2}-x}{l_{1}}=\frac{\cos_{\phi }l_{2}-x}{l_{1}}\nonumber\]
\[\sin\alpha =\frac{\sin{\alpha \beta }l_{2}-y}{l_{1}}=\frac{\sin_{\phi }l_{2}-y}{l_{1}}\nonumber\]
Proporcionar la orientación del robot además de la posición deseada permite resolver para α y β solo en función de x, y y φ.
Como este tipo de soluciones rápidamente se vuelven inútiles con más dimensiones, sin embargo, se puede calcular una solución numérica utilizando un enfoque que veremos más adelante es muy similar a la planificación de rutas en robótica móvil. Una forma de hacerlo es trazar la distancia del efector final desde la solución deseada en el espacio de configuración. Para ello, es necesario resolver la cinemática de avance para cada punto en el espacio de configuración y utilizar la distancia euclidiana hasta el objetivo deseado como altura. En nuestro ejemplo esto sería
\[f_{x,y}(\alpha ,\beta )=\sqrt{(\sin(\alpha +\beta )+\sin(\alpha )-y)^{2}+(\cos(\alpha +\beta)+\cos(a)-x^{2})}\]
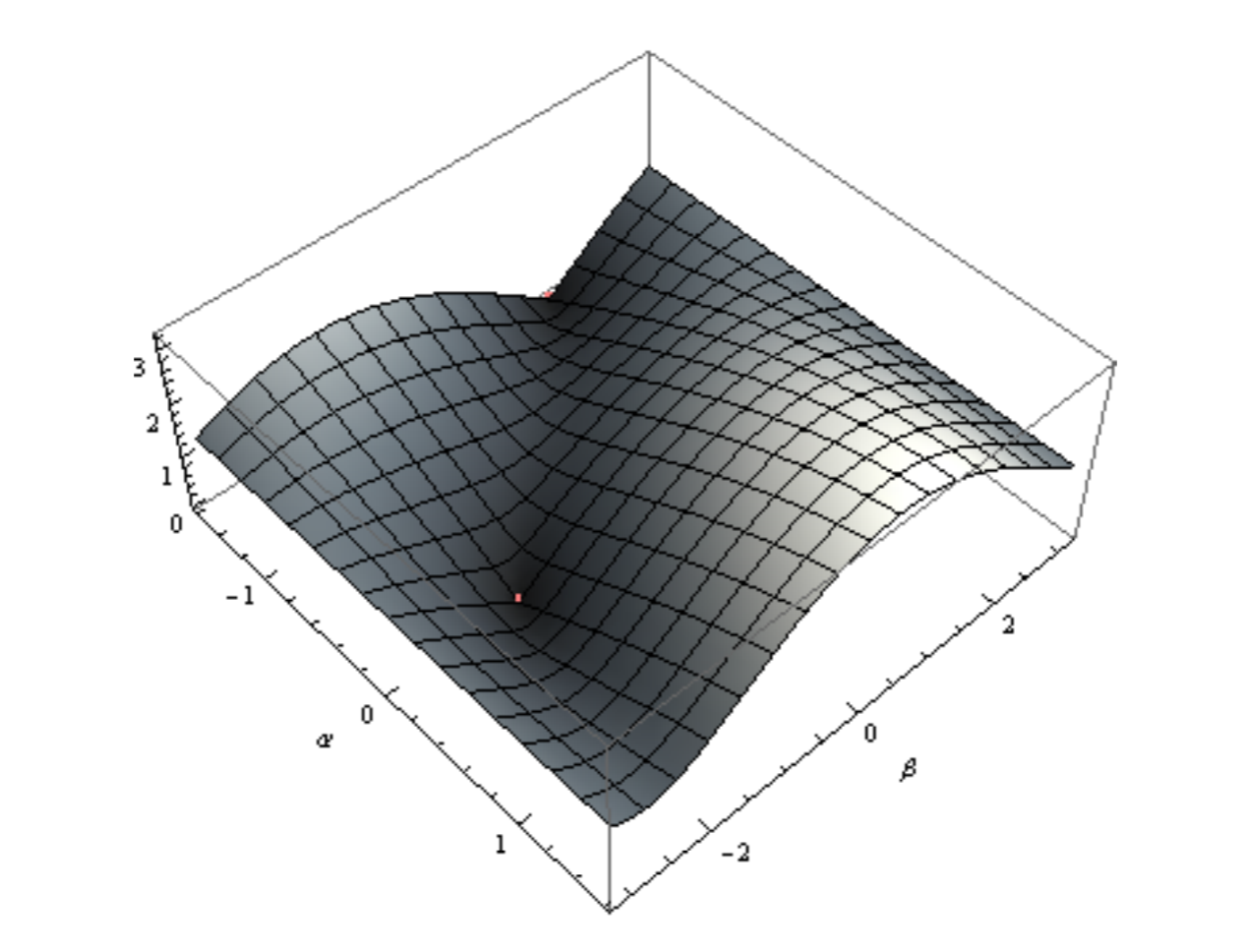
Esto se representa para α = [−π/2, π/2] y β = [−π, π] y x = 1, y = 1 en la Figura 3.4.1. Esta función tiene mínimos, en este caso cero, para valores de α y β que llevan al manipulador a (1, 1). Estos valores son (α → 0, b → −π 2) y (α → −π 2, b → π 2).
Ahora puede pensar en la cinemática inversa como un problema de búsqueda de ruta desde cualquier lugar del espacio de configuración hasta los mínimos más cercanos. Un enfoque formal para hacer esto se discutirá en la Sección 3.5. Cómo encontrar los caminos más cortos en el espacio, es decir, encontrar la ruta más corta para que un robot llegue de A a B será tema del capítulo 4.
3.4.3. Cinemática inversa de Robots Móviles
Como no existe una relación única entre la cantidad de rotación de las ruedas individuales de un robot y su posición en el espacio, pero para plataformas holonómicas simples como un robot en una pista, trataremos el problema de la cinemática inversa al principio solo para las velocidades del marco de coordenadas del robot local.
Primero establezcamos cómo calcular la velocidad necesaria del centro del robot dada una velocidad deseada i en coordenadas mundiales. Podemos transformar la expresión i = T (θ) R multiplicando ambos lados con la inversa de T (θ):
\[T^{-1}(\theta )\xi_{I}=T^{-1}(\theta)T(\theta)\xi _{R}\]
lo que lleva a R = T −1 (θ) I. Aquí
\ [T^ {-1} =\ begin {pmatrix}
cos\ theta & sin\ theta &0\\
-sin\ theta & cos\ theta & 0\\
0 & 0 & 1
\ end {pmatrix}\]
que se puede determinar realizando realmente la inversión matricial o derivando las relaciones trigonométricas del dibujo. Del mismo modo, ahora podemos resolver
\ [\ begin {pmatrix}
x_ {R}\\
y_ {R}\
\ theta
\ end {pmatrix} =\ begin {pmatrix}
\ frac {r\ phi _ {l}} {2} +\ frac {r\ phi _ {r}} {2}\\
0\\ frac {
\ phi _ {r} r} {d} -\ frac {\ frac\ phi _ {l} r} {d}
\ fin {pmatrix}\]
para φ l, φ r
\[\phi _{l}= (2x_{R}-\theta d)/2r\]
\[\phi _{r}= (2x_{R}+\theta d)/2r\]
lo que nos permite calcular la velocidad de rueda del robot en función de un x R y θ deseados, que se puede calcular utilizando (3.4.6).
Obsérvese que este enfoque no nos permite tratar con y R ≠ 0, lo que podría resultar de una velocidad deseada en el marco inercial. Los valores distintos de cero para la traducción en dirección y son simplemente ignorados por la solución cinemática inversa, y conducir hacia un punto específico requiere control de retroalimentación (Sección 3.5.2) o planificación de ruta (Capítulo 4).


