3.5: Cinemática inversa usando Feedback-Control
- Page ID
- 84885
Resolver el problema cinemático inverso para robots móviles no holonómicos requiere que encontremos una secuencia de comandos de accionamiento. Una forma de hacerlo es emplear el control de retroalimentación. En pocas palabras, el control de retroalimentación utiliza el error entre la posición real y la deseada para calcular una pieza de trayectoria que acerca al robot un poco más a su pose deseada. Luego se repite el proceso hasta que el error es marginalmente pequeño. Este enfoque no solo puede ser utilizado para robots móviles, sino también para brazos manipuladores con cinemática que son demasiado complicadas de resolver analíticamente.
3.5.1. Control de retroalimentación para robots móviles
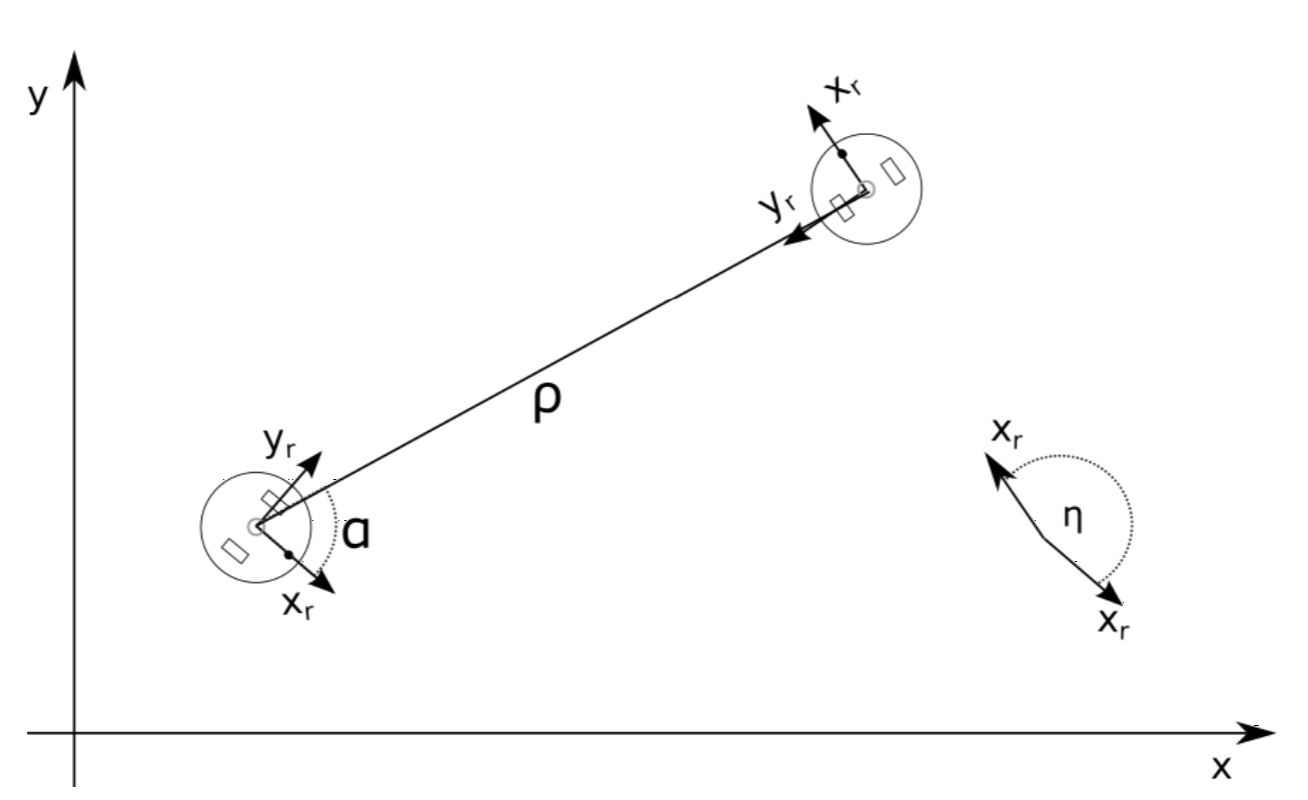
Asumir la posición del robot dada por x r, y r y θ r y la pose deseada como x g, y g y θ g con el subíndice g indicando “meta”. Ahora podemos calcular el error en la pose deseada
\[\rho =\sqrt{(x_{r}-x_{g})^{2}+(y_{r}-y_{g})^{2}}\]
\[\alpha =\tan^{-1}\frac{y_{g}-y_{r}}{x_{g}-x_{r}}-\theta _{r}\nonumber\]
\[\eta =\theta _{g}-\theta _{r}\nonumber\]
que se ilustra en la Figura 3.5.1. Estos errores se pueden convertir directamente en velocidades del robot, por ejemplo usando un controlador proporcional simple con ganancias p1, p2 y p3:
\[x=p_{1}\rho \]
\[\theta =p_{2}\alpha +p_{3}\eta\]
lo que permitirá que el robot conduzca en una curva hasta que alcance la pose deseada.
3.5.2. Técnica jacobiana inversa
El brazo de dos eslabones (Figura 3.2.1) implicaba solo dos parámetros libres, pero ya era bastante complejo de resolver analíticamente si no se especificaba la pose del efector final. Se puede imaginar que las cosas se vuelven muy duras con más grados de libertad o geometrías más complejas. (Los mecanismos en los que algunos ejes se cruzan son más sencillos de resolver que otros, por ejemplo.) Afortunadamente, existen técnicas numéricas simples que funcionan razonablemente bien. Una de ellas conocida es como técnica jacobiana inversa:
Como podemos calcular fácilmente la pose resultante para cada combinación posible de ángulos de articulación usando las ecuaciones cinemáticas hacia adelante, podemos calcular el error entre la pose deseada y la real. Este error en realidad nos proporciona una dirección que el efector final necesita mover. Como solo necesitamos mover pequeños bits a la vez y luego podemos volver a calcular el error, este es un método atractivo para generar una trayectoria que mueva el brazo hacia donde queremos que vaya y con ello resolviendo el problema de la cinemática inversa.
Para ello, necesitamos una expresión que relacione la velocidad deseada del efector final del robot, es decir, la dirección en la que queremos movernos, con la velocidad a la que necesitamos cambiar nuestras articulaciones. Deje que la velocidad de traslación de un robot sea dada por
\ [\ upsilon =\ begin {pmatrix}
x\\
y\\
z
\ end {pmatrix}\]
Como el robot potencialmente no solo puede trasladarse, sino también rotar, también necesitamos especificar su velocidad angular. Que estas velocidades se den como un vector
\ [\ omega =\ comenzar {pmatrix}
\ omega _ {x}\
\ omega _ {y}\
\ omega _ {z}
\ final {pmatrix}\]
Esta notación también se llama tornillo de velocidad. Ahora podemos escribir velocidades de traslación y rotación en un vector 6x1 como (v ω) T. Dejar que los ángulos/posiciones de la articulación sean j = (j 1,..., j n).
Dada una relación entre las velocidades del efector final j y las velocidades de unión J, podemos escribir
\ [\ begin {pmatrix}
\ upsilon &\ omega
\ end {pmatrix} ^ {T} =J (j_ {1},... , j_ {n}) ^ {T}\]
con n el número de articulaciones. J también se conoce como la matriz jacobiana y contiene todas las derivadas parciales que relacionan cada ángulo de articulación con cada velocidad. En la práctica, J parece
\ [\ begin {pmatrix}
\ upsilon\
\ omega
\ end {pmatrix} =\ begin {pmatrix}
\ frac {x} {j_ {1}} &\ cdots &\ frac {x} {j_ {n}}\
\ vdots &\ vdots\\
\ frac {\ omega_ {z}} {j_ {1}} &\ cdots &\ frac {\ omega_ {z} } {j_ {n}}
\ end {pmatrix} (j_ {1},... , j_ {n}) ^ {T}\]
Esta notación es importante ya que nos dice cómo pequeños cambios en el espacio articular afectarán la posición del efector final en el espacio cartesiano. Mejor aún, siempre se puede calcular la cinemática hacia delante de un mecanismo, así como sus derivadas analíticas, lo que nos permite calcular valores numéricos para las entradas de la matriz J para cada posible ángulo/posición conjunta.
Ahora sería deseable invertir simplemente J para calcular las velocidades de unión necesarias para cada velocidad deseada del efector final. Desafortunadamente, J solo es invertible si hay exactamente 6 articulaciones independientes, de modo que J es cuadrática y tiene rango completo. Si este no es el caso, podemos usar la pseudo-inversa en su lugar:
\[J^{+}=\frac{J^{T}}{JJ^{T}}=J^{T}(JJ^{T})^{-1}\]
Como puede ver, J T cancela de la ecuación dejando 1/J, mientras que es aplicable a matrices no cuadráticas.
Esta solución podría o no ser numéricamente estable, dependiendo de los valores actuales de la junta. Si la inversa de J no es matemáticamente factible, hablamos de una singularidad del mecanismo. Esto sucede por ejemplo cuando dos ejes de articulación se alinean, por lo tanto, eliminando efectivamente un grado de libertad del mecanismo, o en el límite del espacio de trabajo. Matemáticamente hablando el rango del jacobiano es menor a seis.
Ahora podemos escribir un controlador de retroalimentación simple que conduzca nuestro error e como la diferencia entre la posición deseada y la real a cero:
\[\Delta j=-J^{+}e\]
Es decir, movemos cada articulación un poquito en la dirección que minimiza e. Se puede ver fácilmente que las velocidades de la junta son solo cero si e se ha convertido en cero. Un problema surge, sin embargo, cuando el efector final tiene que pasar por una singularidad para llegar a su objetivo. Entonces, la solución a J + “explota” y las velocidades conjuntas van al infinito. Para solucionar esto, podemos introducir amortiguación en el controlador.
Esto se puede lograr no solo minimizando el error, sino también las velocidades de las articulaciones. Así, el problema de minimización se convierte en
\[\parallel J\Delta j-e\parallel +\lambda ^{2}\parallel \Delta j\parallel ^{2}\]
donde λ es alguna constante. Se puede demostrar que el controlador resultante que logra esto tiene la forma
\[\Delta j=(J^{T}J+\lambda ^{2}I)^{-1}J^{+}e\]
Esto se conoce como el método Damped Least-Squares. Los problemas con este enfoque son los mínimos locales y las singularidades del mecanismo, lo que podría hacer que esta solución sea inviable.


