4.2: Algoritmos de planificación de rutas

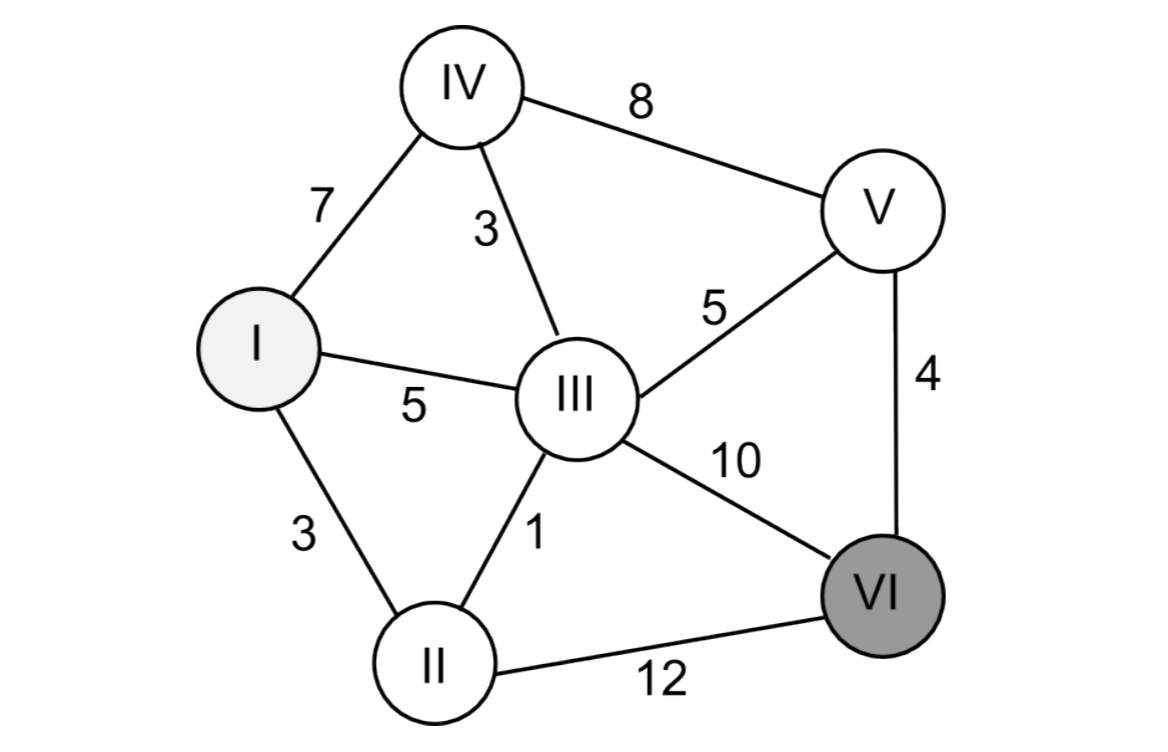
El problema de encontrar una ruta “más corta” de un vértice a otro a través de una gráfica conectada es de interés en múltiples dominios, más prominentemente en internet, donde se utiliza para encontrar una ruta óptima para un paquete de datos. El término “más corto” se refiere aquí al costo mínimo acumulado de borde, que podría ser la distancia física (en una aplicación robótica), el retraso (en una aplicación de red) o cualquier otra métrica que sea importante para una aplicación específica. En la Figura 4.2.1 se muestra un gráfico de ejemplo con bordes arbitrarios.

Figura\(\PageIndex{1}\): Un problema genérico de planeación de ruta desde el vértice I hasta el vértice VI. El camino más corto es I-III-III-V-VI con longitud 13.

4.2.1. Realización del robot

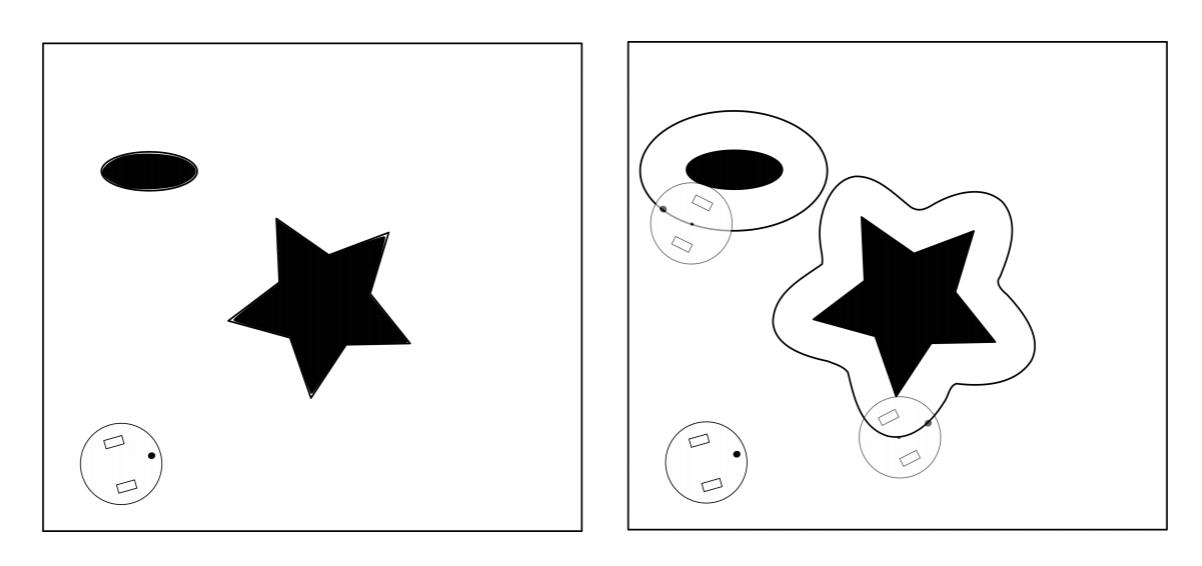
Para hacer frente a la encarnación física del robot, lo que complica el proceso de planificación de ruta, el robot se reduce a una masa puntual y todos los obstáculos en el entorno crecen a la mitad de la extensión más larga del robot desde su centro. Esta representación se conoce como espacio de configuración ya que reduce la representación del robot a sus coordenadas x e y en el plano. Un ejemplo se muestra en la Figura 4.2.2. El espacio de configuración ahora se puede utilizar como base para un mapa de cuadrícula o una representación continua.

Figura\(\PageIndex{2}\): Un mapa con obstáculos y su representación en el espacio de configuración, que se puede obtener haciendo crecer cada obstáculo por la extensión del robot.

4.2.2. Algoritmo de Dijkstra

Uno de los algoritmos más antiguos y simples es el algoritmo de Dijkstra (Dijkstra 1959). Partiendo del vértice inicial donde debería comenzar la ruta, el algoritmo marca a todos los vecinos directos del vértice inicial con el costo para llegar allí. Luego procede desde el vértice con el menor costo a todos sus vértices adyacentes y los marca con el costo para llegar a ellos vía sí mismo si este costo es menor. Una vez que se han verificado todos los vecinos de un vértice, el algoritmo procede al vértice con el siguiente costo más bajo. Una vez que el algoritmo alcanza el vértice objetivo, termina y el robot puede seguir los bordes apuntando hacia el costo de borde más bajo.

En la Figura 4.2.1, Dijkstra marcaría primero los nodos II, III y IV con costo 3, 5 y 7 respectivamente. Entonces seguiría explorando todos los bordes del nodo II, que hasta el momento tiene el menor costo. Esto conduciría al descubrimiento de que el nodo III realmente se puede alcanzar en 3+1 < 5 pasos, y el nodo III se volvería a etiquetar con costo 4. Para evaluar completamente el nodo II, Dijkstra necesita evaluar el borde restante antes de continuar y etiquetar el nodo VI con 3 + 12 = 15.

El nodo con el menor costo es ahora el nodo III (4). Ahora podemos reetiquetar el nodo VI con 14, que es menor que 15, y etiquetar el nodo V con 4 + 5 = 9, mientras que el nodo IV permanece en 4 + 3 = 7. Aunque ya hemos encontrado dos caminos hacia la meta, uno de los cuales mejor que el otro, no podemos detenernos ya que todavía existen nodos con aristas inexploradas y costo general inferior a 14. De hecho, continuar explorando desde el nodo V conduce a una ruta I-III-III-V-VI más corta de costo 13, sin nodos restantes para explorar.

Como Dijkstra no se detendría hasta que no haya nodo con menor costo que el costo actual a la meta, podemos estar seguros de que se encontrará un camino más corto si existe. Podemos decir que el algoritmo está completo.

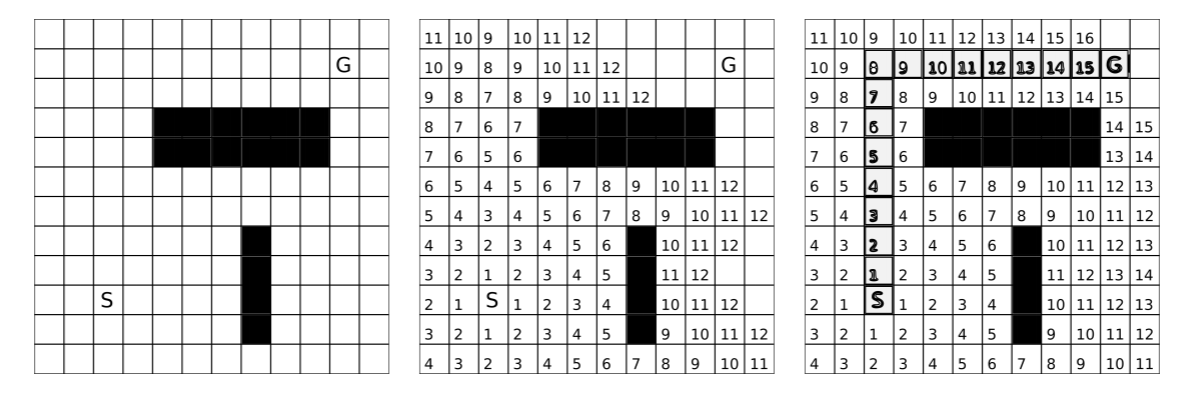
Como Dijkstra siempre explorará primero los nodos con el menor costo general, el entorno se explora comparativamente con un frente de ola que se origina desde el vértice de inicio, llegando finalmente a la meta. Esto es, por supuesto, altamente ineficiente en particular si Dijkstra está explorando nodos lejos de la meta. Esto se puede visualizar agregando un par de nodos a la izquierda del nodo I en la Figura 4.2.1. Dijkstra explorará todos estos nodos hasta que su costo supere el más bajo encontrado para la meta. Esto también se puede observar al observar el algoritmo de Dijkstra en una cuadrícula, como se muestra en la Figura 4.2.3.

Figura\(\PageIndex{3}\): Algoritmo de Dijkstra encontrando una ruta más corta de 'S' a 'G' suponiendo que el robot solo puede viajar lateralmente (no diagonalmente) con un costo de uno por celda de cuadrícula. Tenga en cuenta el escaso número de celdas que permanecen inexploradas una vez que se encuentra el camino más corto (gris), ya que Dijkstra siempre consideraría primero una celda con el costo de ruta más bajo.

4.2.3. A*

En lugar de explorar en todas las direcciones, el conocimiento de una dirección aproximada de la meta podría ayudar a evitar explorar nodos que obviamente son erróneos para un observador humano. Un conocimiento tan especial que tiene tal observador puede codificarse usando una función heurística, una palabra más lujosa para una “regla general”. Por ejemplo, podríamos dar prioridad a los nodos que tienen una distancia estimada menor a la meta que otros. Para ello, marcaríamos cada nodo no solo con la distancia real que nos llevó llegar (como en el algoritmo de Dijkstra), sino también con el costo estimado “a medida que vuela el cuervo”, por ejemplo calculando la distancia euclidiana o la distancia Manhattan entre el vértice que estamos viendo y el vértice de meta . Este algoritmo es conocido como A* (Hart, Nilsson & Raphael 1968). Dependiendo del entorno, A* podría lograr la búsqueda mucho más rápido que el algoritmo de Dijkstra, y realiza lo mismo en el peor de los casos. Esto se ilustra en la Figura 4.2.4 utilizando la métrica de distancia Manhattan, que no permite movimientos diagonales.

Figura\(\PageIndex{4}\): Encontrar un camino más corto de 'S' a 'G' asumiendo que el robot solo puede viajar lateralmente (no diagonalmente) con costo uno por celda de cuadrícula usando el algoritmo A*. Al igual que Dijkstra, A* evalúa solo la celda con el menor costo, pero toma en cuenta una estimación de la distancia restante.

Una extensión de A* que aborda el problema de la costosa replanificación cuando aparecen obstáculos en la trayectoria del robot, se conoce como D* (Stentz 1994). A diferencia de A*, D* parte del vértice de la meta y tiene la capacidad de cambiar los costos de partes del camino que incluyen un obstáculo. Esto permite que D* replanifique alrededor de un obstáculo mientras mantiene la mayor parte del camino ya calculado.

A* y D* se vuelven computacionalmente costosos cuando el espacio de búsqueda es grande, por ejemplo, debido a una resolución de grano fino requerida para la tarea, o las dimensiones del problema de búsqueda son altas, por ejemplo, cuando se planea un brazo con múltiples grados de libertad. Las soluciones a estos problemas son proporcionadas por algoritmos de planificación de rutas basados en muestreo que se describen más adelante.