6.3: Operaciones Básicas de Imagen

Las operaciones básicas de imagen pueden considerarse como un filtro que opera en el dominio de la frecuencia o en el espacio (color). Aunque la mayoría de los filtros operan directamente en el dominio del color, saber cómo afectan al dominio de frecuencia es útil para comprender la función del filtro. Por ejemplo, un filtro que se supone resalta bordes, como el que se muestra en la Figura 6.2.1 debería suprimir las frecuencias bajas, es decir, áreas en las que los valores de color no cambian mucho, y amplificar la información de alta frecuencia, es decir, áreas en las que los valores de color cambian rápidamente. El objetivo de esta sección es proporcionar una comprensión básica de cómo funciona la operación básica de procesamiento de imágenes. Los métodos aquí presentados, aunque siguen siendo válidos, han sido reemplazados por implementaciones más sofisticadas que están ampliamente disponibles como paquetes de software o dentro de software gráfico de escritorio.

Figura\(\PageIndex{1}\): La imagen de un perro dálmata puede ser claramente reconocida por la mayoría de los espectadores a pesar de que las señales de bajo nivel como los bordes solo están presentes para orejas, barbilla y partes de las piernas. Los contornos de los animales se resaltan en una versión invertida de la imagen en el recuadro.

6.3.1. Filtros basados en convolución

Se puede implementar un filtro usando el operador de convolución que convoluciona la función f () con la función g ().

\[f(x) \star g(x)=\int_{-\infty }^{\infty }f(\tau )g(x-\tau )d\tau \]

Luego llamamos a la función g () un filtro. Como quedará más claro más adelante, la convolución desplaza literalmente la función g () a través de la función f () mientras multiplica las dos. Como las imágenes son señales discretas, la convolución suele ser discreta

\[f\left [ x \right ]\star g[x]=\sum_{i=-\infty }^{\infty }f[i]g[x-i]\]

Para señales 2D, como imágenes, la convolución también es bidimensional:

\[f[x,y]\star g[x,y]=\sum_{i=-\infty }^{\infty }\sum_{j=-\infty }^{\infty }f[i,j]g[x-i,y-j]\]

Aunque hemos definido la convolución del infinito negativo al infinito, tanto las imágenes como los filtros suelen ser finitos. Las imágenes están restringidas por su resolución, y los filtros suelen ser mucho más pequeños que las propias imágenes. Además, la convolución es conmutativa, por lo tanto (6.3.3) equivale a

\[f[x,y]\star g[x,y]=\sum_{i=-\infty }^{\infty }\sum_{j=-\infty }^{\infty }f[x-i,y-j]g[i,j]\]

Suavizado gaussiano

Un filtro muy importante es el filtro gaussiano. Tiene la forma de la función de campana gaussiana y se puede almacenar fácilmente en una matriz 2D. Implementar un filtro gaussiano es sorprendentemente simple, por ejemplo, tal como

\ [g (x, y) =\ frac {1} {10}\ begin {pmatrix}
1 & 1 & 1\\
1& 2 &1\\
1 & 1 & 1 & 1
\ end {pmatrix}\]

El uso de este filtro en la Ecuación 6.3.4 en una imagen infinitamente grande f () conduce a

\[f[x,y]\star g[x,y]=\sum_{i=-1 }^{1 }\sum_{j=-1 }^{1 }f[x-i,y-j]g[i,j]\]

(suponiendo que g (0, 0) se dirija al centro de la matriz). Lo que ahora sucede es que cada píxel f (x, y) se convierte en el promedio del de sus vecinos, con su valor anterior ponderado dos veces (como g (0, 0) = 0.2) el de sus vecinos. Más concretamente,

\ [f (x, y) =llf (x+1, y+1) g (-1, -1) +f (x+1, y) g (-1,0) +f (x+1, y-1) g (-1,1) +f (x, y+1) g (0, −1) +f (x, y) g (0,0) +f (x, y−1) g (0,1)
+f (x−1, y+1) g (1, −1) +f (x−1, y) g (1,0) +f (x−1, y−1) g (1,1)\]

Hacer esto para todos x y todos y literalmente corresponde a deslizar el filtro g () a lo largo de la imagen.

En la Figura 6.3.2 se muestra un ejemplo de filtro g (x, y) en acción. El filtro actúa como un filtro de paso bajo, suprimiendo componentes de alta frecuencia. En efecto, se suprime el ruido en la imagen, lo que lleva también a una imagen de borde más suave, que se muestra debajo.

Detección de bordes

La detección de bordes se puede lograr usando otro filtro basado en convolución, el kernel Sobel

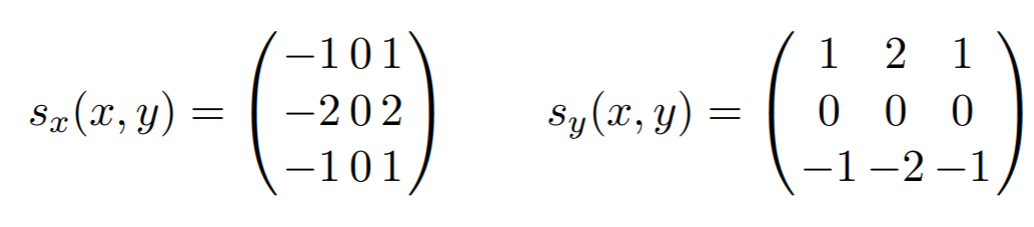
Aquí, s _x (x, y) se puede utilizar para detectar bordes verticales, mientras que s _y (x, y) resalta los bordes horizontales. Por lo tanto, los detectores de bordes, como el detector de bordes Canny, ejecutan al menos dos de dichos filtros sobre una imagen para detectar bordes horizontales y verticales.

Figura\(\PageIndex{2}\): Una imagen ruidosa antes (arriba a la izquierda) y después de filtrar con un núcleo gaussiano (arriba a la derecha). Las imágenes de borde correspondientes se muestran debajo.

Diferencia de Gaussianos

Un método alternativo para detectar bordes es el método Diferencia de Gaussianos (DoG). La idea es restar dos imágenes que han sido filtradas cada una usando un kernel gaussiano con diferente ancho. Ambos filtros suprimen la información de alta frecuencia y su diferencia, por lo tanto, conduce a una señal filtrada de paso banda, de la cual se han eliminado las frecuencias bajas y altas. Como tal, un filtro DoG actúa como un algoritmo de detección de bordes capaz. Aquí, un kernel suele ser de cuatro a cinco veces más ancho que el otro, por lo tanto, actúa como un filtro mucho más fuerte.

Las diferencias de los gaussianos también se pueden utilizar para aproximar el Laplaciano de Gaussiano, es decir, la suma de las segundas derivadas de un núcleo gaussiano. Aquí, un núcleo es aproximadamente 1.6 veces más ancho que el otro. Las características de paso de banda de DoG y LOG son importantes ya que resaltan la información de alta frecuencia, como los bordes, pero suprimen el ruido de alta frecuencia en la imagen.

6.3.2. Operaciones basadas en umbrales

Para encontrar objetos con cierto color o intensidad de borde, el umbral de una imagen conducirá a una imagen binaria que contenga regiones “verdadero-falso” que se ajusten a los criterios deseados. Los umbrales hacen uso de operadores como >, <, ≤, ≥ y combinaciones de los mismos. También existen versiones adaptativas que adaptarían los umbrales localmente, por ejemplo, para suplir las condiciones de iluminación cambiantes.

Aunque la fijación de umbrales es engañosamente simple, encontrar valores de umbral correctos es un problema difícil. En particular, los valores de píxel reales cambian drásticamente con las condiciones de iluminación cambiantes y no existe tal cosa como “rojo” o “verde” al inspeccionar los valores reales bajo diferentes condiciones.

Figura\(\PageIndex{3}\): Ejemplos de operadores morfológicos de erosión y dilatación y combinaciones de los mismos.

6.3.3. Operaciones Morfológicas

Otra clase de filtros son los operadores morfológicos que consisten en un kernel que describe la estructura de la operación (esto puede ser tan simple como una matriz de identidad) y una regla sobre cómo cambiar un valor de píxel basado en los valores en la vecindad definida por el kernel.

Importantes operadores morfológicos son la erosión y dilatación. El operador de erosión asigna un valor de píxel con el valor mínimo que puede encontrar en la vecindad definida por el kernel. El operador de dilatación asigna un valor de píxel con el valor máximo que puede encontrar en la vecindad definida por el núcleo. Esto es útil, por ejemplo, para rellenar agujeros en una línea o eliminar el ruido. Una dilatación seguida de una erosión se conoce como “Cierre” y una erosión seguida de una dilatación como “Apertura”. Restar imágenes erosas y dilatadas entre sí también puede servir como detector de bordes. Ejemplos de tales operadores se muestran en la Figura 6.3.3.