7.3: Reconocimiento de Línea

¿Por qué las líneas son una característica útil? Como verás en el siguiente capítulo, el reto clave para estimar la pose de un robot es la odometría poco confiable, en particular a la hora de girar. Aquí, un simple sensor de infrarrojos que mide la distancia a una pared puede proporcionar al robot una mejor idea de lo que realmente sucedió. De igual manera, si un robot tiene la capacidad de rastrear marcadores en el entorno usando la visión, obtiene otra estimación de cuánto se está moviendo realmente. Cómo se puede fusionar la información de la odometría y otros sensores no sólo para localizar al robot, sino también para crear mapas de su entorno, será el foco del resto de este libro.

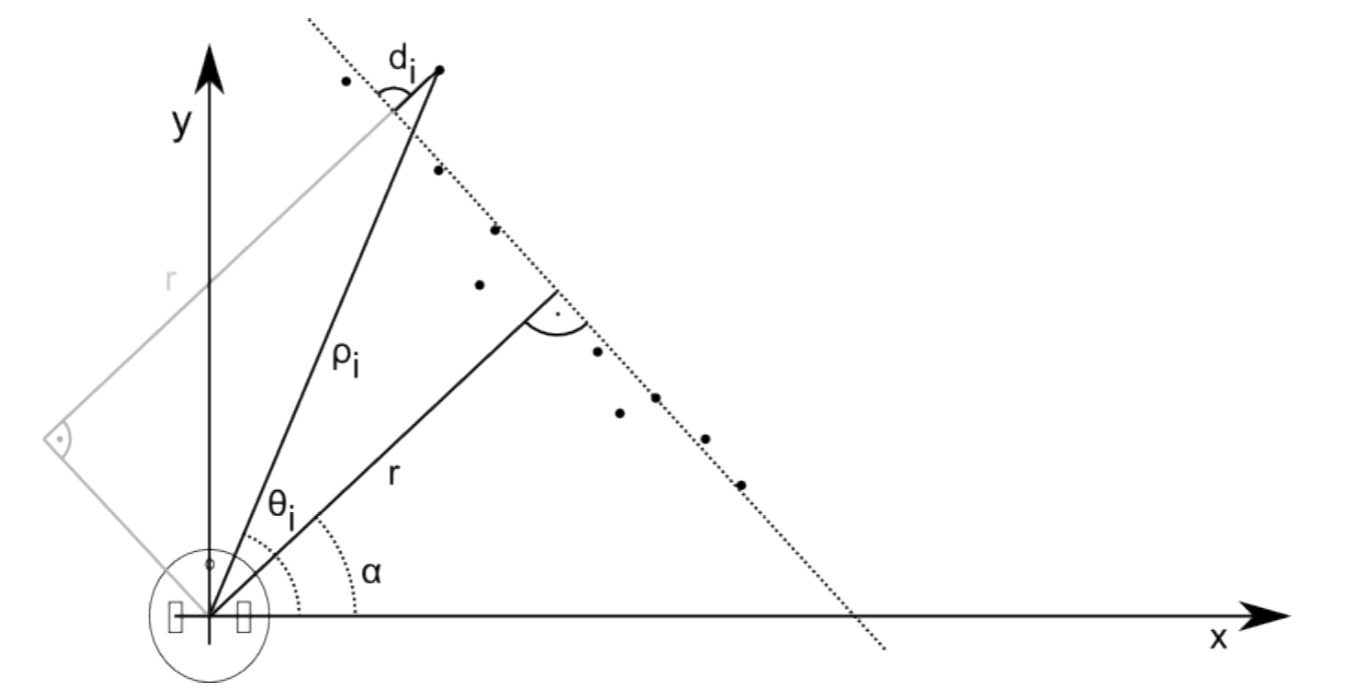
Un escáner láser o dispositivo similar apuntado contra una pared devolverá un conjunto de N puntos en la posición (xi, yi) en el sistema de coordenadas del robot. Estos puntos también se pueden representar en coordenadas polares (ρi, θi). Ahora podemos imaginar una línea que recorre estos puntos que se parametriza con una distancia r y un ángulo α. Aquí, r es la distancia del robot a la pared y α su ángulo. Como todos los sensores son ruidosos, cada punto tendrá distancia di de la línea “óptima” que recorre los puntos. Estas relaciones se ilustran en la Figura 7.2.1.

7.3.1. Ajuste de línea usando mínimos cuadrados

Usando trigonometría simple ahora podemos escribir

\[\rho _{i} \cos(\theta _{i}-\alpha )-r=d_{i}\]

Diferentes candidatos de línea —parametrizados por r y α— tendrán diferentes valores para d _i. Ahora podemos escribir una expresión para el error total S _{r, α} como

\[S_{r,\alpha }=\sum_{i=1}^{N}d_{i}^{2}=\sum_{i}^{}(\rho _{i}\cos(\theta _{i}-\alpha )-r)^{2}\]

Figura\(\PageIndex{1}\): Nube de puntos 2D registrada por un escáner láser o dispositivo similar. Una línea (discontinua) se ajusta a través de los puntos en un sentido de mínimos cuadrados.

Aquí, cuadramos cada error individual para tener en cuenta el hecho de que un error negativo, es decir, un punto a la izquierda de la línea, es tan malo como un error positivo, es decir, un punto a la derecha de la línea óptima. Para optimizar S _{r, α,} necesitamos tomar las derivadas parciales con respecto a r y α, ponerlas a cero y resolver el sistema resultante de ecuaciones para r y α.

\[\frac{∂S}{∂\alpha }=0 \\ \frac{∂S}{∂r}=0\]

Aquí, el símbolo indica que estamos tomando una derivada parcial. Resolver para r y α está involucrado, pero es posible (Siegwart et al. 2011):

\[\alpha =\frac{1}{2}atan\left ( \frac{\frac{1}{N}\sum \rho _{i}^{2}sin2\theta _{i}-\frac{2}{N^{2}}\sum \sum\rho _{i}\rho _{j}cos\theta _{i}sin_{j}}{\frac{1}{N}\sum \rho _{i}^{2}cos2\theta _{i}-\frac{1}{N^{2}}\sum \sum\rho _{i}\rho _{j}cos(\theta _{i}+\theta _{j})} \right )\]

y

\[r=\frac{\sum \rho _{i}cos(\theta _{i}-\alpha )}{N}\]

Por lo tanto, podemos calcular la distancia y orientación de una pared capturada por nuestros sensores de proximidad en relación con las posiciones del robot o la altura y orientación de una línea en una imagen a partir de una colección de puntos que creemos que podrían pertenecer a una línea.

Figura\(\PageIndex{2}\): Algoritmo de división y fusión. Ajuste inicial de mínimos cuadrados de una línea (izquierda). Dividir el conjunto de datos en el punto con el error más alto (después de elegir una dirección) permite ajustar dos líneas con un error general menor.

Este enfoque se conoce como el método de mínimos cuadrados y se puede utilizar para ajustar datos a cualquier modelo paramétrico. El enfoque general es describir el ajuste entre los datos y el modelo en términos de un error. El mejor ajuste minimizará esta función, que por lo tanto tendrá una derivada cero en este punto. Si el resultado no se puede obtener analíticamente como en este ejemplo, se deben utilizar métodos numéricos para encontrar el mejor ajuste que minimice el error cuadrático.

7.3.2. Algoritmo de división y fusión

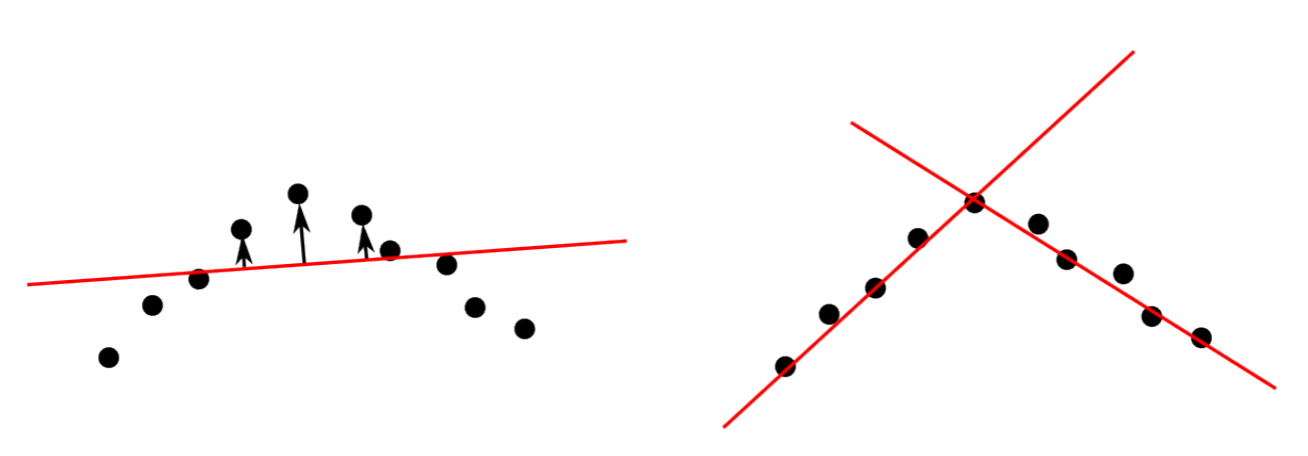
Un problema clave con este enfoque es que a menudo no está claro cuántas líneas hay y dónde comienza una línea y dónde termina. Mirando a través de la cámara, por ejemplo, veremos líneas verticales correspondientes a esquinas de pared y horizontales que corresponden a intersecciones de pared-suelo y al horizonte; usando un sensor de distancia, el robot podría detectar una esquina. Por lo tanto, necesitamos un algoritmo que pueda separar las nubes de puntos en múltiples líneas. Un enfoque posible es encontrar el valor atípico con la desviación más fuerte de una línea ajustada y dividir la línea en este punto. Esto se ilustra en la Figura 7.3.2. Esto se puede hacer iterativamente hasta que cada línea no tenga valores atípicos por encima de un cierto umbral.

Figura\(\PageIndex{3}\): Muestra Aleatoria y Consenso (RASAC). Las líneas aleatorias se evalúan contando el número de puntos cercanos (” inliers”), las líneas más oscuras se ajustan mejor.

7.3.3. RASAC: Muestra Aleatoria y Consenso

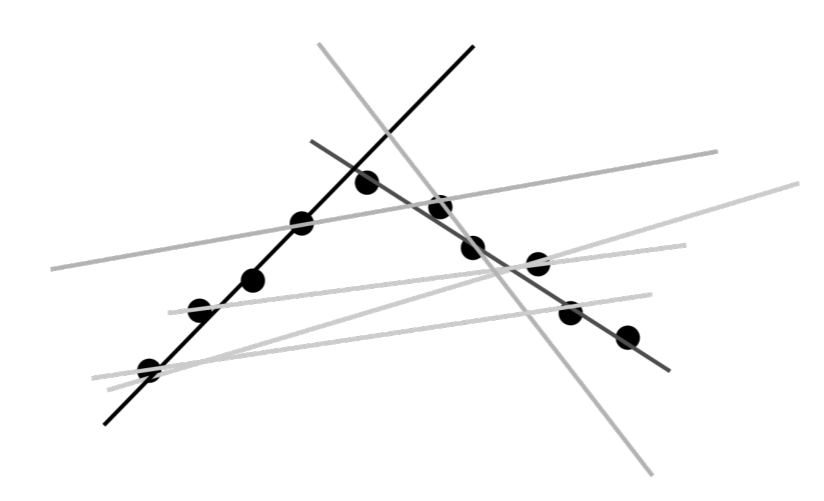
Si el número de “valores atípicos” es grande, un ajuste de mínimos cuadrados generará malos resultados ya que generará el “mejor” ajuste que acomode tanto a “inliers” como a “valores atípicos”. Además, los algoritmos de división y fusión fallarán ya que son extremadamente susceptibles al ruido: dependiendo de los parámetros reales, cada valor atípico dividirá una línea potencial en dos. Una solución a este problema es muestrear aleatoriamente posibles líneas y mantener aquellas que satisfagan cierta calidad deseada dada por el número de puntos que están algo cerca del mejor ajuste. Esto se ilustra en la Figura 7.3.3, con líneas más oscuras correspondientes a mejores ajustes. Por lo general, el RASAC requiere dos parámetros, a saber, el número de puntos requeridos para considerar que una línea es un ajuste válido, y el máximo di de una línea para considerar un punto un inlier y no un valor atípico. El algoritmo procede de la siguiente manera: seleccionar dos puntos aleatorios del conjunto y conectarlos con una línea. Crecer esta línea por di en ambas direcciones y contar el número de inliers. Repita esto hasta que se encuentren una o más líneas que tengan suficiente número de inliers, o se alcance un número máximo de iteraciones.

El algoritmo de RASAC es bastante fácil de entender en la aplicación de ajuste de línea, pero se puede utilizar para ajustar modelos paramétricos arbitrarios a datos de cualquier dimensión. Aquí, su principal fortaleza es hacer frente a datos ruidosos.

Dado que el RASAC es aleatorio, encontrar un ajuste realmente bueno llevará bastante tiempo. Por lo tanto, el RASAC generalmente se usa solo como un primer paso para obtener una estimación inicial, que luego se puede mejorar con algún tipo de optimización local, como por ejemplo mínimos cuadrados, p.

7.3.4. La transformación de Hough

La transformada de Hough se puede entender mejor como un esquema de votación para adivinar la parametrización de una entidad como una línea, círculo u otra curva (Duda & Hart 1972). Por ejemplo, una línea podría estar representada por y = mx+c, donde m y c son el gradiente y el desplazamiento. Un punto en este espacio de parámetros (o “espacio-casa”) corresponde entonces a una línea específica en x−y-space (o “image-space”). La transformada Hough ahora procede de la siguiente manera: por cada píxel de la imagen que podría ser parte de una línea, por ejemplo, píxeles blancos en una imagen umbral después del filtrado de Sobel, construya todas las líneas posibles que se crucen con este punto. (Dibujar una imagen de esto parecería una estrella). Cada una de estas líneas tiene un specifc m y c asociados a ella, para lo cual podemos agregar un punto blanco en Houghspace. Seguir haciendo esto por cada píxel de una línea en una imagen dará muchos pares m − c, pero solo uno que es común entre todos esos píxeles de la línea en la imagen: los parámetros m−c reales de esta línea. Pensando en la cantidad de veces que un punto fue resaltado en Hough-space como brillo, convertirá una línea en el espacio de la imagen en un punto brillante en el espacio Hough (y al revés). En la práctica, se elige una representación polar para las líneas. Esto se muestra en la Figura 7.4.1. La transformación de Hough también generaliza a otra parametrización como los círculos.