8.2: Propogación de errores

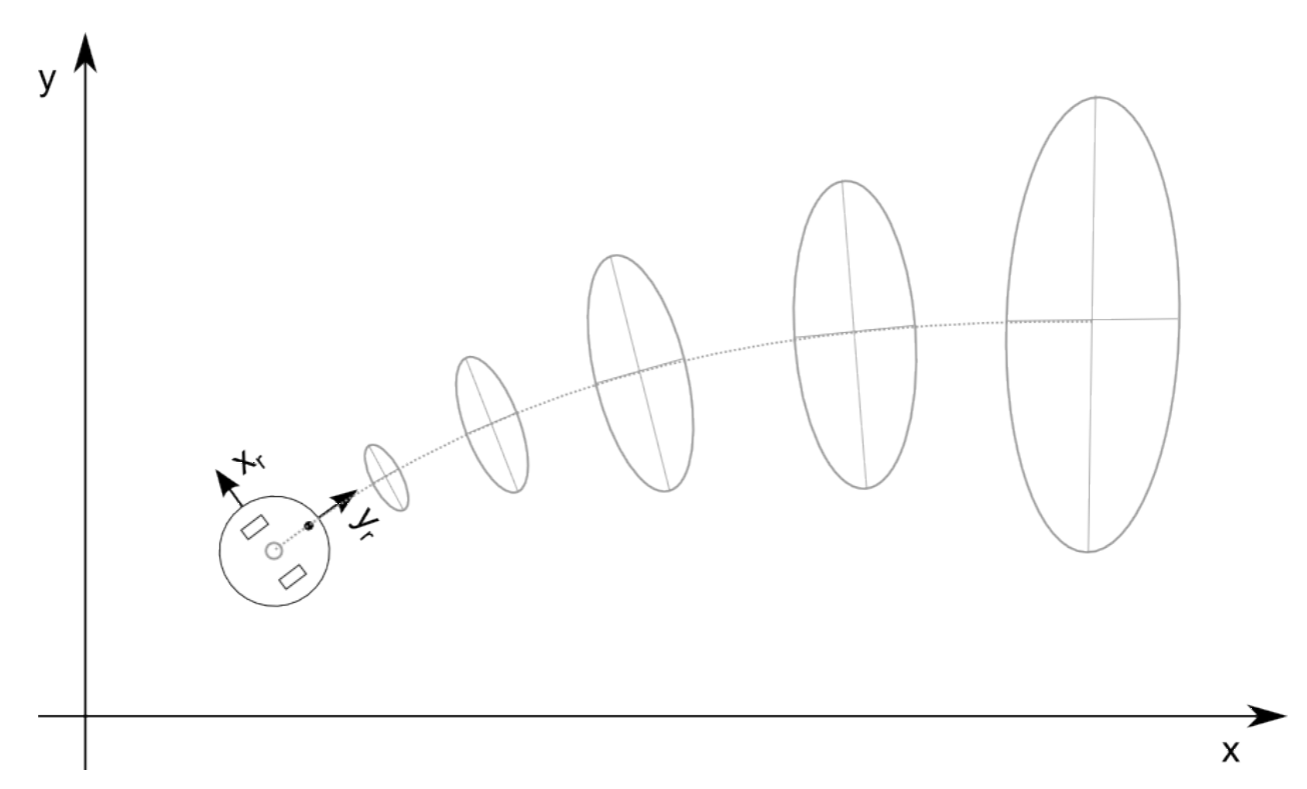
Resulta que la Distribución Gaussiana es muy apropiada para modelar procesos aleatorios prominentes en robótica: las mediciones de posición y distancia del robot. Un robot de rueda diferencial que conduce a lo largo de una línea recta, y está sujeto a deslizamiento, en realidad aumentará su incertidumbre cuanto más conduzca. Inicialmente en una ubicación conocida, el valor esperado (o media) de su posición será cada vez más incierto, correspondiendo a una varianza creciente. Esta varianza obviamente está relacionada de alguna manera con la varianza del mecanismo subyacente, a saber, la rueda deslizante y el ruido del codificador (comparablemente pequeño). Curiosamente, veremos que su varianza crece mucho más rápido ortogonal a la dirección del robot, ya que los pequeños errores en la orientación tienen un efecto mucho mayor que los pequeños errores en la dirección longitudinal. Esto se ilustra en la Figura 8.2.1.

De manera similar, al estimar la distancia y el ángulo a una entidad de línea a partir de datos de nubes de puntos, la incertidumbre de las variables aleatorias que describen la distancia y el ángulo a la línea están algo relacionadas con la incertidumbre de cada punto medido en la línea. Estas relaciones son capturadas formalmente por la ley de propagación de errores.

Figura\(\PageIndex{1}\): Distribución normal bidimensional que representa la creciente incertidumbre a medida que el robot se mueve. Si bien comenzando con la misma incertidumbre en x e y, el gran efecto de pequeños errores en la orientación permite que el error crezca más rápido en la dirección y del robot

La intuición clave detrás de la ley de propagación de errores es que la varianza de cada componente que contribuye a una variable aleatoria debe ponderarse en función de la fuerza que este componente influye en esta variable aleatoria. Las mediciones que tienen poco efecto sobre la variable aleatoria agregada también deberían tener poco efecto en su varianza y viceversa. “Cuán fuertemente” algo afecta a otra cosa puede expresarse por la proporción de cuán pequeños cambios de algo se relacionan con pequeños cambios en otra cosa. Esto no es otra cosa que la derivada parcial de algo con respecto a otra cosa. Por ejemplo, sea y = f (x) una función que mapee una variable aleatoria x, por ejemplo, una lectura de sensor, a una variable aleatoria y, por ejemplo, una característica. Deje que la desviación estándar de x esté dada por σ _x. Luego podemos calcular la varianza σ ² _y por

\[\sigma _{y}^{2}=\left ( \frac{∂f}{∂x} \right )^{2}\sigma _{x}^{2}\]

En caso de que y = f (x) sea una función multivariable que mapea n entradas a m salidas, las varianzas se convierten en matrices de covarianza. Una matriz de covarianza contiene la varianza de cada variable a lo largo de su diagonal y es cero en caso contrario, si las variables aleatorias no están correlacionadas. Entonces podemos escribir

\[Σ^{Y}=JΣ^{X}J^{T}\]

donde σ ^X y σ ^Y son las matrices de covarianza que contienen las varianzas de las variables de entrada y salida, respectivamente, y J es una matriz jacobiana mxn, que contiene las derivadas parciales f _i /x _j. Como J tiene n columnas, cada fila contiene derivadas parciales con respecto a x ₁ a x _n.

8.2.1. Ejemplo: Ajuste de línea

Consideremos un ejemplo de estimación del ángulo α y la distancia r de una línea a partir de un conjunto de puntos dados por (ρ _i, θ _i) usando las Ecuaciones 7.3.4—7.3.5. Ahora podemos expresar la relación de los cambios de una variable como ρ _i con los cambios en α mediante

\[\frac{∂\alpha }{∂\rho _{i}}\]

Del mismo modo, podemos calcular α/θ _i, r/ρ _i y r/θ _i. En realidad podemos hacer esto, porque hemos derivado expresiones analíticas para α y r en función de θ _i y ρ _i en el Capítulo 7.

Ahora estamos interesados en derivar ecuaciones para calcular la varianza de α y r en función de las varianzas de las mediciones de distancia. Supongamos que cada medición de distancia ρ _i tiene varianza σ ² _ρi y cada medida angular θ _i tiene varianza σ ² _θi. Ahora queremos calcular σ ² _α como la suma ponderada de σ ² _ρi y σ ² _θi, cada una ponderada por su influencia en α. De manera más general, si tenemos I variables de entrada X _i y K variables de salida Y _k, la matriz de covarianza de las variables de salida σ _Y se puede expresar como σ ² _Y = f ² /X σ ² _X donde σ _X es la matriz de covarianza de variables de entrada y J es una matriz jacobiana de una función f que calcula Y a partir de X y tiene la forma

\ [J=\ begin {bmatrix}
\ frac {f_ {1}} {X_ {1}} &\ cdots &\ frac {f_ {1}} {X_ {1}}\\ vdots &\ cdots &\ vdots
\\ frac {f_ {K}} {X_ {1}} &
\ cdots &\ frac {f_ {K}} {X_ {1}} &\ cdots &\ frac ac {f_ {K}} {X_ {1}}
\ end {bmatrix}\]

En el ejemplo de ajuste de línea F _X contendría las derivadas parciales de α con respecto a todas las ρ _i (i-entradas) seguidas de las derivadas parciales de α con respecto a todas las θ _i en la primera fila. En la segunda fila, F _X sostendría los derivados parciales de r con respecto a ρ _i seguido de los derivados parciales de r con respecto a θ _i. Como hay dos variables de salida, α y r, y 2I variables de entrada (cada medición consiste en un ángulo y distancia), F _X es una matriz de 2 x (2I).

El resultado es, por lo tanto, una matriz de covarianza 2x2 que contiene las varianzas de α y r en su diagonal.

8.2.2. Ejemplo: Odometría

Mientras que el ejemplo de ajuste de líneas demostró un mapeo de muchos toone, la odometría requiere calcular la varianza que resulta de múltiples mediciones secuenciales. La propagación de errores nos permite aquí no sólo expresar la posición del robot, sino también la varianza de esta estimación. Nuestra “lista de lavado” para esta tarea se ve de la siguiente manera:

1. ¿Cuáles son las variables de entrada y cuáles son las variables de salida?
2. ¿Cuáles son las funciones que calculan la salida a partir de la entrada?
3. ¿Cuál es la varianza de las variables de entrada?

Como es habitual, describimos la posición del robot mediante una tupla (x, y, θ). Estas son las tres variables de salida. Podemos medir la distancia que recorre cada rueda ∆s _r y ∆s _l en función de las garrapatas del codificador y el radio de rueda conocido. Estas son las dos variables de entrada. Ahora podemos calcular el cambio en la posición del robot calculando

\[\Delta x=\Delta scos(\theta +\Delta \theta /2)\]

\[\Delta y=\Delta ssin(\theta +\Delta \theta /2)\]

\[\Delta \theta =\frac{\Delta s_{r}-\Delta s_{l}}{b}\]

con

\[\Delta s =\frac{\Delta s_{r}+\Delta s_{l}}{2}\]

La posición del nuevo robot viene dada por

\ [f (x, y,\ theta,\ Delta s_ {r},\ Delta s_ {l}) =\ izquierda [x, y,\ theta\ derecha] ^ {T} +\ comenzar {bmatrix}
\ Delta x &\ Delta y &\ Delta\ theta
\ final {bmatrix} ^ {T}\]

Así tenemos ahora una función que relaciona nuestras mediciones con nuestras variables de salida. Lo que complica las cosas aquí es que las variables de salida son una función de sus valores anteriores. Por lo tanto, su varianza no sólo depende de la varianza de las variables de entrada, sino también de la varianza previa de las variables de salida. Por lo tanto, necesitamos escribir

\[Σ_{p'}=∇_{p}fΣ_{p}∇_{p}f^{T}+∇_{\Delta_{r,l}}fΣ_{\Delta }∇_{\Delta_{r,l}}f^{T}\]

El primer término es la propagación del error desde una posición p = [x, y, θ] a una nueva posición p 0. Para ello necesitamos calcular las derivadas parciales de f con respecto a x, y y θ. Esta es una matriz 3x3

\ [_ {p} f=\ begin {bmatrix}
\ frac {f} {x} &\ frac {f} {y} &\ frac {f} {\ theta}\ end {bmatrix}
=\ begin {bmatrix}
1 & 0 & -\ Delta ssin (\ theta +\ Delta\ theta /2)\\
0& 1 y Delta\ scos (\ theta +\ Delta\ theta /2)\\
0& 0 & 1
\ end {bmatrix}\]

El segundo término es la propagación del error del deslizamiento real de la rueda. Esto requiere calcular las derivadas parciales de f con respecto a ∆s _r y ∆s _l, que es una matriz 3x2. La primera columna contiene las derivadas parciales de x, y, θ con respecto a ∆s _r. La segunda columna contiene las derivadas parciales de x, y, θ con respecto a ∆s _l:

\ [_ {\ Delta _ {r, l}} f=\ begin {bmatrix}
\ frac {1} {2}\ cos (\ theta +\ frac {\ Delta\ theta /2} {b}) -\ frac {\ Delta s} {2b}\ sin (\ theta +\ frac {\ Delta\ theta} {b}) &\ frac {1} 2}\ cos (\ theta +\ frac {\ Delta\ theta /2} {b}) -\ frac {\ Delta s} {2b}\ sin (\ theta +\ frac {\ Delta\ theta} {b})\
\ frac {1} {2}\ sin ( \ theta +\ frac {\ Delta\ theta /2} {b}) +\ frac {\ Delta s} {2b}\ sin (\ theta +\ frac {\ Delta\ theta} {b}) &\ frac {1} {2}\ sin (\ theta +\ frac {\ Delta\ theta /2} {b}) +\ frac {\ Delta s} 2b}\ sin (\ theta +\ frac {\ Delta\ theta} {b})\
\ frac {1} {2} & -\ frac {1} {2}
\ end {bmatrix}\]

Finalmente, necesitamos definir la matriz de covarianza para el ruido de medición. Como el error es proporcional a la distancia recorrida, podemos definir σ _∆by

\ [σ_ {\ Delta} =\ begin {bmatrix}
k_ {r}\ izquierda |\ Delta s_ {r}\ derecha | & 0\\
0 & k_ {l}\ izquierda |\ Delta s_ {l}\ derecha |
\ end {bmatrix}\]

Aquí _kr y k _l son constantes que necesitan ser encontradas experimentalmente y | · | indicando el valor absoluto de la distancia recorrida. También asumimos que el error de las dos ruedas es independiente, lo que se expresa por los ceros en la matriz.

Ahora tenemos todos los ingredientes para la Ecuación 8.2.10, lo que nos permite calcular la matriz de covarianza de la pose del robot como se muestra en la Figura 8.2.1.