9.2: Localización de Markov

Calcular la probabilidad de estar en una ubicación determinada dada la probabilidad de ciertas observaciones no es otra cosa como una probabilidad condicional. Existe una manera formal de describir tales situaciones: Regla de Bayes (Sección C.2):

\[P(A|B)=\frac{P(A)P(B|A)}{P(B)}\]

9.2.1. Actualización de Percepción

¿Cómo se mapee esto en un marco de localización? Supongamos que el evento A es equivalente a estar en una ubicación específica loc. Supongamos también que el evento B corresponde al evento para ver una hazaña de característica en particular. Ahora podemos reescribir la regla de Bayes para

\[P(loc|feat)=\frac{P(loc)P(feat|loc)}{P(feat)}\]

Reformulando la regla de Bayes de esta manera, podemos calcular la probabilidad de estar en locación loc, dado que vemos característica hazaña. Esto se conoce como Actualización de Percepción. Por ejemplo, loc podría corresponder a la puerta 1, 2 o 3, y hazaña podría ser el evento de detectar una puerta. ¿Qué necesitamos saber para hacer uso de esta ecuación?

1. Necesitamos conocer la probabilidad previa de estar en la ubicación loc P (loc)
2. Necesitamos saber la probabilidad de ver la entidad en esta ubicación P (feat|loc)
3. Necesitamos la probabilidad de encontrar la característica feat P (feat)

Figura\(\PageIndex{1}\): Un robot que se localiza usando un “detector de puerta” en un mapa conocido. Arriba: Al encontrarse con una puerta, el robot puede estar frente a cualquiera de las tres puertas. Medio: Al conducir hacia la derecha, las distribuciones gaussianas que representan su ubicación también se desplazan hacia la derecha y se ensanchan, lo que representa una creciente incertidumbre. Abajo: Después de detectar la segunda puerta, el robot puede descartar hipótesis que no están frente a la puerta y gana certeza sobre su ubicación.

Empecemos con (3), que podría ser la parte más confusa de la información que necesitamos recopilar. La respuesta es simple, no importa lo que sea P (feat), se cancelará ya que la probabilidad de estar en cualquiera de las ubicaciones posibles tiene que sumar hasta 1. (Una explicación más simple, aunque menos precisa, sería que la probabilidad de percibir una característica es constante y por lo tanto no importa.)

La probabilidad previa de estar en locación loc, P (loc), se denomina modelo de creencia. En el caso del ejemplo de 3 puertas, es el valor de la distribución gaussiana debajo de la puerta correspondiente a loc.

Finalmente, necesitamos conocer la probabilidad de ver la hazaña característica en la ubicación loc P (feat|loc). Si su sensor fuera perfecto, esta probabilidad es simplemente 1 si la característica existe en esta ubicación, o 0 si la característica no se puede observar en esta ubicación. Si su sensor no es perfecto, P (feat|loc) corresponde a la probabilidad de que el sensor vea la característica si existe.

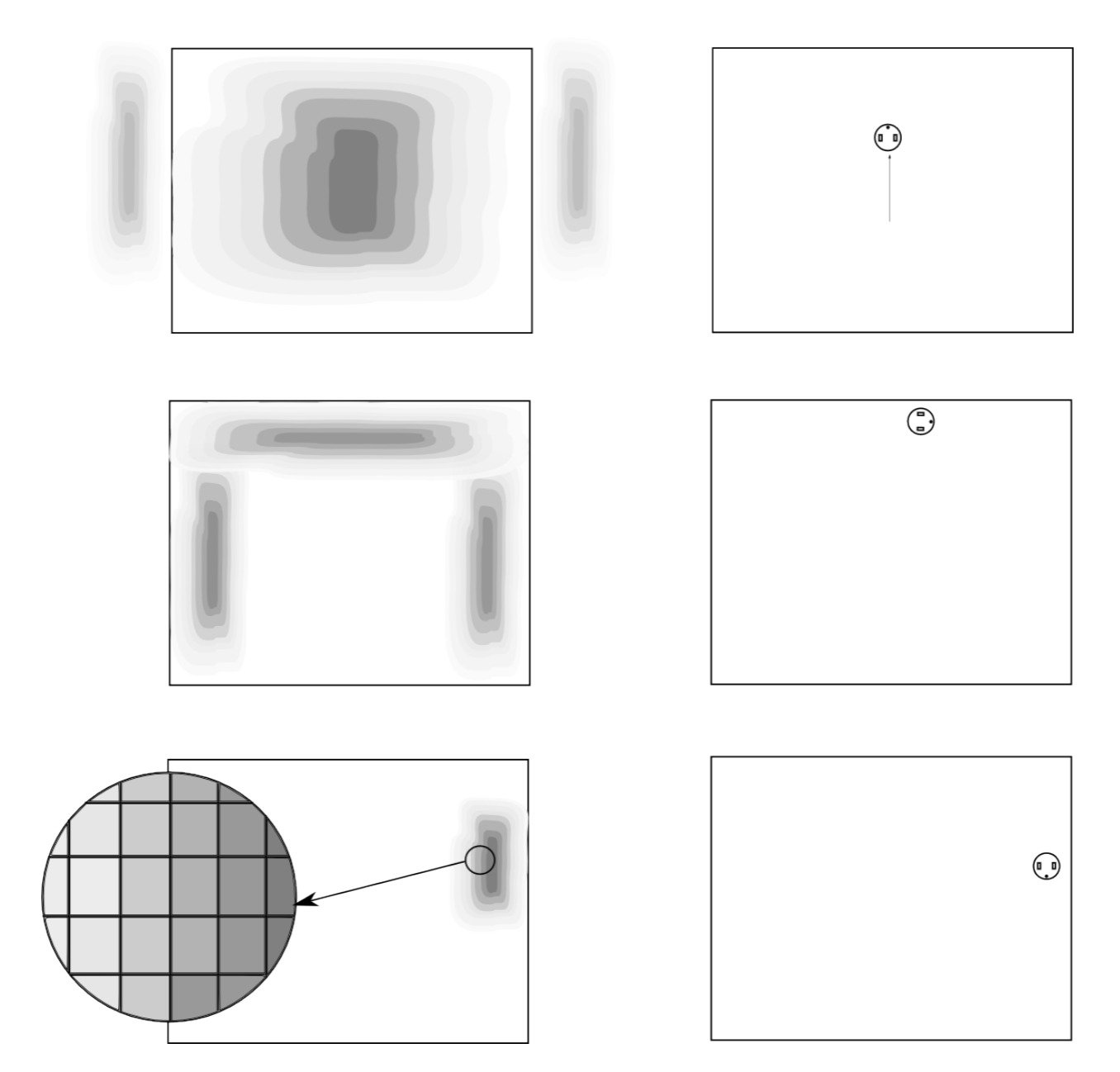
La última pieza faltante es la mejor manera de representar las posibles ubicaciones. En el ejemplo gráfico de la Figura 9.2.1 asumimos distribuciones gaussianas para cada ubicación posible. Alternativamente, también podemos discretizar el mundo en una cuadrícula y calcular la probabilidad de que el robot esté en cualquiera de sus celdas. En nuestro mundo de 3 puertas, podría tener sentido elegir celdas de rejilla que tengan solo el ancho de una puerta.

9.2.2. Actualización de Acción

Una de las suposiciones en el experimento de pensamiento anterior fue que sabemos con certeza que el robot se movió a la derecha. Ahora estudiaremos más formalmente cómo tratar la incertidumbre a partir del movimiento. Recordemos que la entrada de odometría es sólo otro sensor que suponemos que tiene una distribución gaussiana; si nuestro odómetro nos dice que el robot viajó un metro, podría haber viajado un poco menos o un poco más, con probabilidad decreciente. Por lo tanto, podemos calcular la probabilidad posterior de que el robot se mueva de una posición loc' a loc dada su entrada odómetro odo:

\[P(loc'->loc|odo)=P(loc'->loc)P(odo|loc'->loc)/P(odo)\]

Esta es nuevamente la regla de Bayes. La probabilidad incondicional P (loc'− > loc) es la probabilidad previa de que el robot haya estado en la ubicación loc'. El término P (odo|loc'− > loc) corresponde a la probabilidad de obtener odómetro leyendo odo después de viajar de una posición loc' a loc. Si obtener una lectura de la cantidad odo es razonable para la distancia de loc' a loc esta probabilidad es alta. Si no es razonable, por ejemplo si la distancia es mayor de lo que es físicamente posible, esta probabilidad debería ser muy baja.

Como la ubicación del robot es incierta, el verdadero desafío es ahora que el robot podría haber estado potencialmente en todas partes para empezar. Por lo tanto, tenemos que calcular la probabilidad posterior P (loc|odo) para todas las posiciones posibles loc'. Esto se puede lograr sumando todas las ubicaciones posibles:

\[P(loc|odo)=\sum_{loc'}^{}P(loc'->loc)P(odo|loc'->loc)\]

En otras palabras, la ley de probabilidad total requiere que consideremos todas las ubicaciones posibles en las que el robot podría haber estado. Este paso se conoce como Actualización de Acción. En la práctica no necesitamos calcular esto para todas las ubicaciones posibles, sino solo aquellas que sean técnicamente factibles dada la velocidad máxima del robot. Observamos también que la notación suma corresponde técnicamente a una convolución (Sección C.3) de la distribución de probabilidad de la ubicación del robot en el entorno con la distribución de probabilidad de error de odometría del robot.

9.2.3. Resumen y Ejemplos

Ahora hemos aprendido dos métodos para actualizar la distribución de creencias de dónde podría estar el robot en el entorno. Primero, un robot puede usar puntos de referencia externos para actualizar su posición. Esto se conoce como actualización de la percepción y se basa en la exteriocepción. Segundo, un robot puede observar sus sensores internos. Esto se conoce como actualización de acciones y se basa en la propiocepción. La combinación de actualizaciones de acción y percepción se conoce como Localización de Markov. Se puede pensar en la actualización de acción para aumentar la incertidumbre de la posición del robot y la actualización de percepción para encogerla. (También puede pensar en la actualización de acciones como una versión discreta del modelo de propagación de errores). También aquí estamos utilizando el modelo cinemático robótico y el modelo de ruido de su odómetro para calcular P (odo|loc'− > loc).

Figura\(\PageIndex{2}\): Un ambiente de oficina que consta de dos habitaciones conectadas por un pasillo. Un mapa topológico está superimpuesto.

Ejemplo\(\PageIndex{1}\): Topological Map

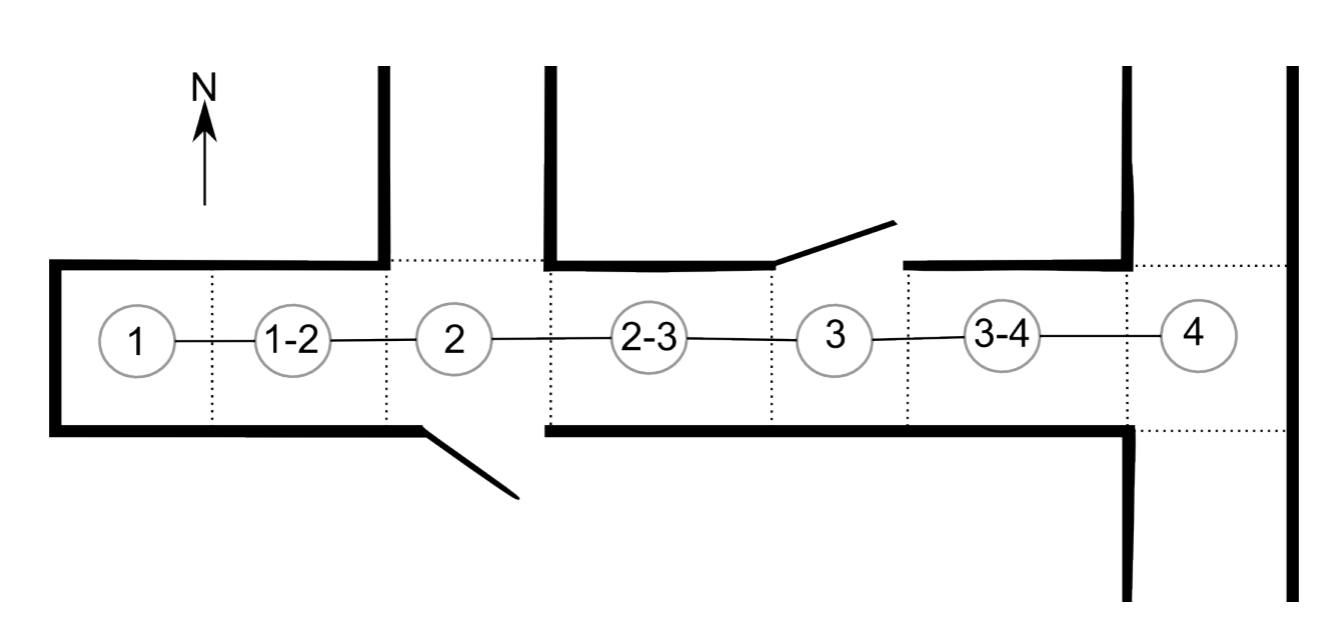
Este ejemplo describe uno de los primeros sistemas robóticos reales exitosos que empleó Markov Location en un entorno de oficina. El experimento se describe con más detalle en un artículo de 1995 de AI Magazine (?). El ambiente de oficina consistió en dos salas y un corredor que puede modelarse mediante un mapa topológico (Figura 9.2.2). En un mapa topológico, las áreas en las que puede estar el robot se modelan como vértices, y las conexiones navegables entre ellas se modelan como bordes de una gráfica. La ubicación del robot ahora se puede representar como una distribución de probabilidad sobre los vértices de esta gráfica.

El robot tiene las siguientes capacidades de detección:

• Puede detectar una puerta cerrada a su izquierda o derecha.
• Puede detectar una puerta abierta a su izquierda o derecha.
• Puede detectar si se trata de un pasillo abierto.

Mesa	Muro	Cerrada Dr	Abrir Dr	Abrir Hwy	Vestíbulo
Nada Detectado	70%	40%	5%	0.1%	30%
Detectada Puerta Cerrada	30%	60%	0%	0%	5%
Detectada Puerta Abierta	0%	0%	90%	10%	15%
Pasillo Abierto Detectado	0%	0%	0.1%	90%	50%

Cuadro\(\PageIndex{1}\): Probabilidades condicionales del robot Dervish detectando ciertas características en el laboratorio de Stanford.

Desafortunadamente, los sensores del robot no son para nada confiables. Los investigadores han encontrado experimentalmente las probabilidades de obtener una cierta respuesta del sensor para posiciones físicas específicas usando su robot en su entorno. Estos valores se proporcionan en la Tabla 9.2.1.

Por ejemplo, la tasa de éxito para detectar una puerta cerrada es solo del 60%, mientras que un vestíbulo parece una puerta abierta en el 15% de los ensayos. Estos datos corresponden a la probabilidad condicional de detectar una determinada característica dada una determinada ubicación.

Consideremos ahora la siguiente distribución inicial del estado de creencia: p (1 − 2) = 0.8 y p (2 − 3) = 0.2. Aquí, 1 − 2 etc. se refiere a la posición en el mapa topológico en la Figura 9.2.2. Ya sabes que el robot mira hacia el este con certeza. El robot ahora conduce por un tiempo hasta que reporta “abrir pasillo a su izquierda y abrir puerta a su derecha”. Esto en realidad corresponde a la ubicación 2, pero el robot de hecho puede estar en cualquier lugar. Por ejemplo, existe un 10% de probabilidad de que la puerta abierta sea de hecho un pasillo abierto, es decir, el robot está realmente en la posición 4. ¿Cómo podemos calcular la nueva distribución de probabilidad de la ubicación del robot? Aquí están las posibles trayectorias que podrían ocurrir:

El robot podría pasar de 2−3 a 3, 3−4 y finalmente 4. Hemos elegido esta secuencia ya que la probabilidad de detectar una puerta abierta a su derecha es cero para 3 y 3 − 4, lo que deja la posición 4 como la única opción si el robot ha comenzado en 2 − 3. Para que esta hipótesis sea cierta, es necesario que hayan ocurrido los siguientes eventos, sus probabilidades se dan entre paréntesis:

1. El robot debe haber comenzado a 2 − 3 (20%)
2. No haber visto la puerta abierta a la izquierda de 3 (5%) y no haber visto la pared a la derecha (70%)
3. No haber visto el muro a su izquierda (70%) y no haber visto el muro a su derecha en el nodo 3 − 4 (70%)
4. Identificar correctamente el pasillo abierto a su izquierda (90%) y confundir el pasillo abierto a su derecha con una puerta abierta (10%)

En conjunto, la probabilidad de que el robot llegue de la posición 2 − 3 a la posición 4 viene dada por 0.2 × 0.05 × 0.7 × 0.7 × 0.7 × 0.7 × 0.9 × 0.1 = 0.03%, eso es muy improbable.

El robot también podría pasar de 1 − 2 a 2, 2 − 3, 3, 3 − 4 o 4. Podemos evaluar estas hipótesis de manera similar:

• La probabilidad de que detecte correctamente el pasillo abierto y la puerta en la posición 2 es de 0.9 × 0.9, por lo que la posibilidad de estar en la posición 2, habiendo comenzado en 1−2, es de 0.8×0.9×0.9 = 64%.
• El robot no puede haber terminado en la posición 2 − 3, 3 y 3 − 4 porque la posibilidad de ver una puerta abierta en lugar de una pared en el lado derecho es cero en todos estos casos.
• Para alcanzar la posición 4, el robot debe haber comenzado en 1−2 tiene una probabilidad de 0.8. El robot no debe haber visto el pasillo a su izquierda y la puerta abierta a su derecha al pasar la posición 2. La probabilidad para esto es 0.001×0.05. El robot debe entonces no haber detectado nada en 2−3 (0.7× 0.7), nada en 3 (0.05×0.7), nada en 3−4 (0.7×0.7), y finalmente confundió el pasillo de su derecha con una puerta abierta en la posición 4 (0.9 × 0.1). Multiplicados juntos, este resultado es muy poco probable.

Dada esta información, ahora podemos calcular la probabilidad posterior de estar en cierta ubicación en el mapa topológico sumando las probabilidades para cada camino posible para llegar allí.

Ejemplo\(\PageIndex{2}\): Grid-Based Markov Localization

En lugar de usar un mapa topológico grueso, también podemos modelar el entorno como una cuadrícula de grano fino. Cada celda está marcada con una probabilidad correspondiente a la probabilidad de que el robot esté en esta ubicación exacta (Figura 9.2.3). Suponemos que el robot es capaz de detectar paredes con cierta certeza. Las imágenes de la columna derecha muestran la ubicación real del robot. Inicialmente, el robot no ve una pared y por lo tanto podría estar en casi cualquier lugar. El robot ahora se mueve hacia el norte. La actualización de acción ahora propaga la probabilidad de que el robot esté en algún lugar hacia arriba. Tan pronto como el robot se encuentra con la pared, la actualización de la percepción aumenta la probabilidad de estar cerca de una pared. Como hay cierta incertidumbre asociada con el detector de pared, el robot no solo puede estar directamente en la pared, sino en cualquier lugar —con probabilidad decreciente— cerca. Como la actualización de la acción implicó un movimiento continuo hacia el norte, la probabilidad de estar cerca del muro sur es casi nula. Luego, el robot realiza un giro a la derecha y viaja a lo largo de la pared en sentido horario. Tan pronto como golpea el muro este, es casi seguro acerca de su posición, que luego vuelve a disminuir.

Figura\(\PageIndex{3}\): Localización de Markov en una cuadrícula. La columna de la izquierda muestra la probabilidad de estar en una celda específica como valor de gris (los colores oscuros corresponden a altas probabilidades). La columna derecha muestra la ubicación real del robot. Las flechas indican movimiento previo. Inicialmente, se desconoce la posición del robot, pero el movimiento registrado hacia arriba hace que las posiciones en la parte superior del mapa sean más probables. Después de que el robot se ha encontrado con una pared, las posiciones alejadas de las paredes se vuelven poco Después de movimientos hacia la derecha y hacia abajo, las posiciones posibles se han reducido a un área pequeña.