15.1: Variables aleatorias y Distribuciones de Probabilidad

Las variables aleatorias pueden describir variables discretas, como el resultado de lanzar un dado, o variables continuas como medir una distancia. Para conocer la probabilidad de que una variable aleatoria tenga un determinado resultado, podemos repetir el experimento muchas veces y registrar las variables aleatorias resultantes, es decir, los valores reales de la variable aleatoria, y el número de veces que ocurrieron. Para un dado perfectamente cúbico veremos que la variable aleatoria puede contener números naturales del 1 al 6, que tienen la misma probabilidad de 1/6.

La función que describe la probabilidad de que una variable aleatoria tome ciertos valores se denomina distribución de probabilidad. Como la probabilidad de todas las posibles variaciones aleatorias en el experimento de dados es la misma, los dados siguen lo que llamamos una distribución uniforme. Más exactamente, como los resultados de rodar un dado son números discretos, en realidad es una distribución uniforme discreta. La mayoría de las variables aleatorias no están distribuidas uniformemente, pero algunas variables son más probables que otras. Por ejemplo, al considerar una variable aleatoria que describe la suma de dos dados lanzados simultáneamente, podemos ver que la distribución es cualquier cosa menos uniforme:

\ [2:1 +1\ fila derecha\ frac {1} {6}\ frac {1} {6}\
3:1 +2, 2+1\ fila derecha 2\ frac {1} {6}\ frac {1} {6}\
4:1 + 3, 2 + 2, 3 + 1\ fila derecha 3\ frac {1} {6}\ frac {1}\ frac {1}\ frac {1} {6}\\
5:1 + 4, 2 + 3, 3 + 2, 4 + 1\ fila derecha 4\ frac {1} {6}\ frac {1} {6}\
6:1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1\ fila derecha 5\ frac {1} {6}\ frac {1} {6}\
7:1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1\ fila derecha 6\ frac {1} {6}\ frac {1} {6}\
8:1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1\ fila derecha 5\ frac {1} {6}\ frac {1} {6}\
9:1 + 4, 2 + 3, 3 + 2, 4 + 1\ fila derecha 4\ frac {1} {6}\ frac {1} {6}\ frac {1} {6}\
10:1 + 3, 2 + 2, 3 + 1\ fila derecha 3\ frac {1} {6}\ frac {1} {6}\
11:1 +2, 2+1\ fila derecha 2\ frac {1} {6}\ frac {1} {6}\
12:1 +1\ fila derecha\ frac {1} {6}\ frac {1} {6}\\\ nonumber\]

Como se puede ver, hay muchas más posibilidades de sumar hasta un 7 que a un 3, por ejemplo Si bien es posible almacenar distribuciones de probabilidad como esta como una tabla de consulta para predecir el resultado de un experimento (o el de una medición), también podemos calcular la suma de dos procesos aleatorios analíticamente (Sección C.3).

15.1.1. La distribución normal

Una de las distribuciones más destacadas es la Distribución Gaussiana o Normal. La distribución Normal se caracteriza por una media y una varianza. Aquí, la media corresponde al valor promedio de una variable aleatoria (o el pico de la distribución) y la varianza es una medida de cuán ampliamente se distribuyen las variables alrededor de la media (o el ancho de la distribución). La distribución Normal se define mediante la siguiente función

\[f(x)=\frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{-\frac{(x-\mu)^{2} }{2\sigma ^{2}}}\]

donde µ es la media y σ ² la varianza. (σ por sí solo se conoce como la desviación estándar.) Entonces, f (x) es la probabilidad de que una variable aleatoria X tenga valor x.

\[\mu =\int_{-\infty }^{\infty }xf(x)dx\]

o en otras palabras, cada posible valor x es ponderado por su verosimilitud y sumado.

Figura\(\PageIndex{1}\): Distribución normal para diferentes varianzas y µ = 0.

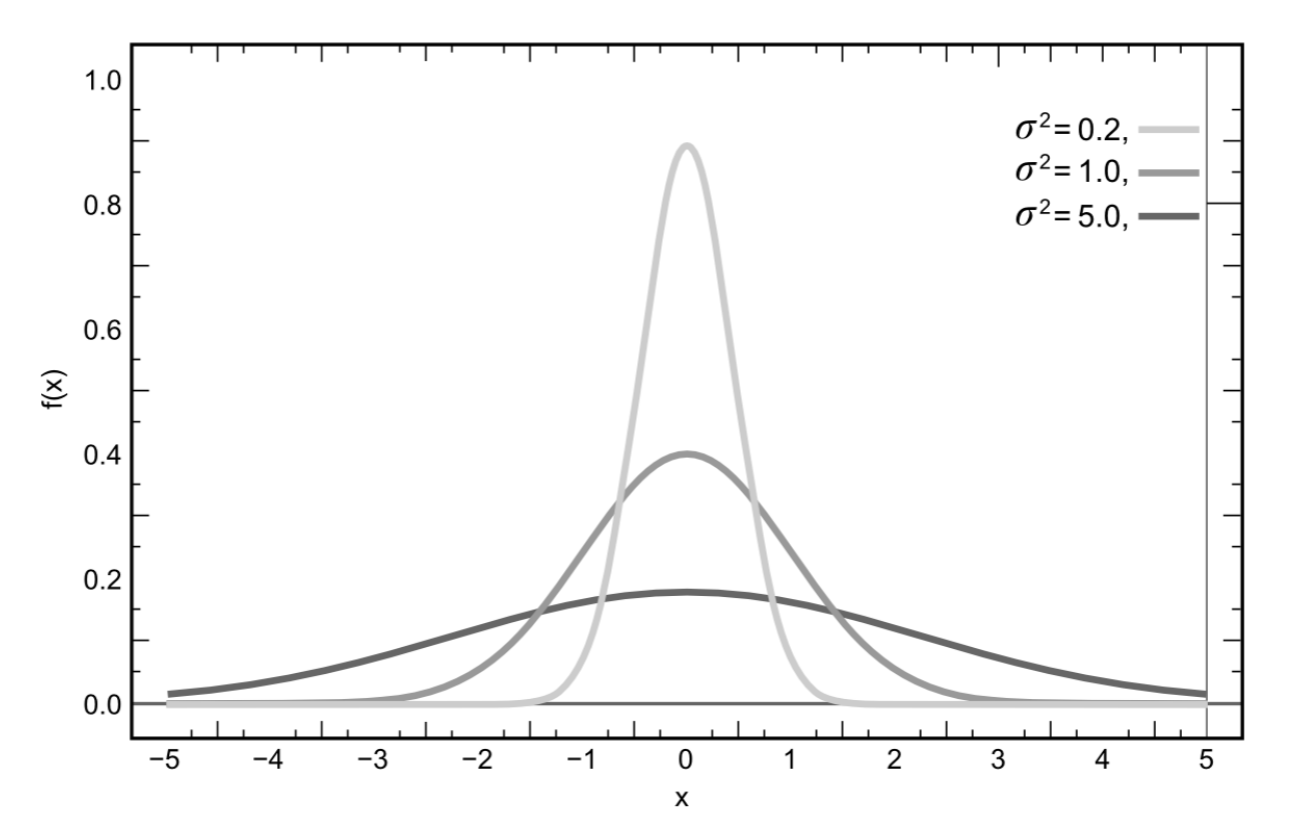
La varianza se calcula por

\[\sigma ^{2}=\int_{-\infty }^{\infty }(x-\mu )^{2}f(x)dx\]

o en otras palabras, calculamos la desviación de cada variable aleatoria a partir de la media, la cuadramos y la pesamos por su verosimilitud. Aunque resulta tentador realizar este cálculo también para el experimento de dados dobles, el valor resultante es cuestionable, ya que el experimento de dados dobles no sigue una distribución Normal. Esto lo sabemos, porque en realidad enumeramos todos los resultados posibles. Para otros experimentos, como las calificaciones en las clases que estás tomando, no sabemos cuál es la distribución real.

15.1.2. Distribución normal en dos dimensiones

La Distribución Normal no se limita a procesos aleatorios con una sola variable aleatoria. Por ejemplo, la posición X/Y de un robot en el plano es un proceso aleatorio con dos dimensiones. En el caso de una distribución multivariada con k dimensiones, la variable aleatoria X es un vector k-dimensional de variables aleatorias, µ es un vector k-dimensional de medias, y σ se reemplaza por σ, una matriz de covarianza dimensional k-por-k (una matriz que lleva las varianzas de cada variable aleatoria en su diagonal).