3.2: Teorema de Varignon

Última actualización
Guardar como PDF

Page ID: 83849

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El teorema de Varignon, también llamado a menudo el principio de los momentos, es una herramienta muy útil en los cálculos de momentos escalares. En los casos en que la distancia perpendicular es difícil de determinar, el Teorema de Varignon ofrece una alternativa para encontrar esa distancia.

En su forma básica, el Teorema de Varignon afirma que si tenemos dos o más fuerzas concurrentes, la suma de los momentos que cada fuerza crea alrededor de un solo punto será igual al momento creado por la suma de esas fuerzas alrededor del mismo punto.

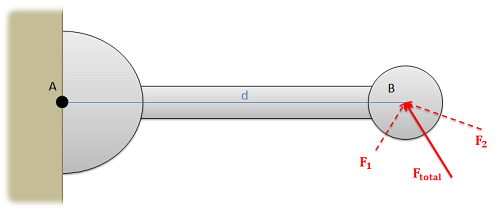
Una palanca con un extremo unido a la pared, con dos fuerzas diferentes aplicadas a su extremo libre. También se muestra un tercer vector, la suma de esas dos fuerzas, actuando sobre el extremo libre. — Figura\(\PageIndex{1}\): Si la suma de\(\vec{F}_1\) y\(\vec{F}_2\) es\(\vec{F}_{total}\), entonces podemos suponer que la suma de los momentos sobre el punto A ejercidos por\(\vec{F}_1\) y\(\vec{F}_2\) será igual al momento ejercido sobre el punto A por\(\vec{F}_{total}\).

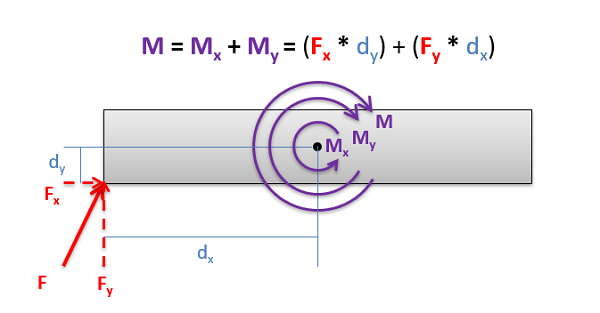
En su superficie esto no parece tan útil, pero en la práctica a menudo usaremos este teorema a la inversa al descomponer una fuerza en componentes (siendo los componentes un conjunto de fuerzas concurrentes). Podemos resolver por el momento ejercido por cada componente (donde la distancia perpendicular\(d\) es más fácil de encontrar) y luego simplemente sumar los momentos de cada componente para encontrar el momento a partir de la fuerza original.

Una forma rectangular tiene una fuerza aplicada hacia arriba y hacia la derecha en la esquina inferior izquierda, provocando la rotación de la forma alrededor de su punto central. Además del vector de la fuerza aplicada, se muestran los componentes x e y de dicha fuerza, así como las distancias verticales y horizontales desde el punto de aplicación de la fuerza hasta el punto central. — Figura\(\PageIndex{2}\): Al encontrar el momento de fuerza\(\vec{F}\) alrededor del punto central, será más fácil descomponer la fuerza en componentes y encontrar los momentos de cada componente en lugar de tratar de encontrar la distancia perpendicular directamente usando relaciones geométricas complejas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/XcxXyPv7Wp4.

Ejemplo\(\PageIndex{1}\)

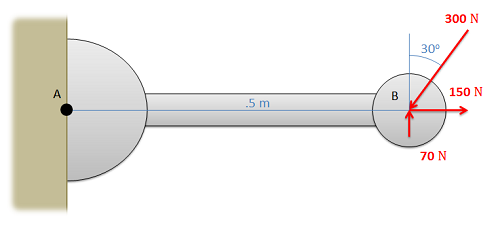
Usa el Teorema de Varignon para encontrar el momento en que las fuerzas del diagrama a continuación ejercen sobre el punto A.

Una palanca de 0.5 metros de largo está unida a una pared en un extremo; el centro de esta región de contacto es el punto A. Se aplican simaltáneamente tres fuerzas al extremo libre: una de magnitud 70 N hacia arriba, una de magnitud 150 N a la derecha, y una de magnitud 300 N hacia abajo y hacia la izquierda, en un ángulo de 30 grados desde la vertical. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una palanca está unida a una pared en un extremo, y se aplican 3 fuerzas diferentes al extremo libre de la palanca, a 0.5 m del punto de contacto de la base con la pared (punto A).

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/JIpgZGxJWu4.

Ejemplo\(\PageIndex{2}\)

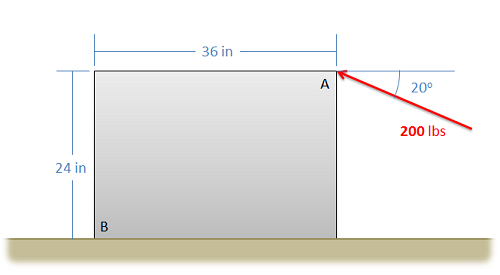
Usa el Teorema de Varignon para encontrar el momento en que la fuerza en el diagrama a continuación ejerce sobre el punto B.

Un rectángulo de 24 por 36 pulgadas descansa con su lado más largo horizontal. Se aplica una fuerza de magnitud de 200 lb hacia arriba y hacia la izquierda, formando un ángulo de 20 grados con la horizontal, en la esquina superior derecha del rectángulo, punto A. La esquina inferior izquierda del rectángulo se marca como punto B. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Una caja rectangular, que puede considerarse una forma bidimensional, se asienta sobre una superficie plana y experimenta una fuerza aplicada a su esquina superior derecha.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/jpaLEprFndA.