3.6: Análisis de Equilibrio para un Cuerpo Rígido

Última actualización
Guardar como PDF

Page ID: 83819

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para un cuerpo rígido en equilibrio estático —es decir, un cuerpo indeformable donde las fuerzas no son concurrentes— la suma tanto de las fuerzas como de los momentos que actúan sobre el cuerpo debe ser igual a cero. La adición de momentos (a diferencia de partículas, donde solo miramos las fuerzas) agrega otro conjunto de posibles ecuaciones de equilibrio, lo que nos permite resolver por más incógnitas en comparación con los problemas de partículas.

Los momentos, como las fuerzas, son vectores. Esto significa que nuestra ecuación vectorial necesita ser desglosada en componentes escalares antes de que podamos resolver las ecuaciones de equilibrio. En un problema bidimensional, el cuerpo solo puede tener rotación en sentido horario o antihorario (correspondiente a rotaciones alrededor del\(z\) eje). Esto significa que un cuerpo rígido en un problema bidimensional tiene tres ecuaciones de equilibrio posibles; es decir, la suma de componentes de fuerza en las\(y\) direcciones\(x\) y, y los momentos alrededor del\(z\) eje. La suma de cada uno de estos será igual a cero.

Para un problema bidimensional, rompemos nuestra ecuación de fuerza de un vector en dos ecuaciones de componentes escalares. \[ \sum \vec{F} \, = \, 0 \]

\[ \sum F_x \, = \, 0\, ; \,\, \sum F_y \, = \, 0 \]La ecuación vectorial de un momento se convierte en una ecuación escalar de un solo momento. \[ \sum \vec{M} \, = \, 0 \]

\[ \sum M_z \, = \, 0 \]

Si nos fijamos en un problema tridimensional aumentaremos a seis el número de ecuaciones de equilibrio posibles. Existen tres ecuaciones de equilibrio para la fuerza, donde la suma de los componentes en las\(z\) direcciones\(x\)\(y\),, y debe ser igual a cero. El cuerpo también puede tener momentos alrededor de cada uno de los tres ejes. El segundo conjunto de tres ecuaciones de equilibrio establece que la suma de los componentes de momento alrededor de los\(z\) ejes\(x\)\(y\),, y también debe ser igual a cero.

Rompemos las fuerzas en tres ecuaciones de componentes. \[ \sum \vec{F} \, = \, 0 \]

\[ \sum F_x \, = \, 0 \, ; \,\, \sum F_y \, = \, 0 \, ; \,\, \sum F_z \, = \, 0 \]

Entonces también dividimos los momentos en tres ecuaciones de componentes. \[ \sum \vec{M} \, = \, 0 \]

\[ \sum M_x \, = \, 0 \, ; \,\, \sum M_y \, = \, 0 \, ; \,\, \sum M_z \, = \, 0 \]

Encontrar las ecuaciones de equilibrio

Al igual que con las partículas, el primer paso para encontrar las ecuaciones de equilibrio es dibujar un diagrama de cuerpo libre del cuerpo que se está analizando. Este diagrama debería mostrar todos los vectores de fuerza que actúan sobre el cuerpo. En el diagrama de cuerpo libre, proporcione valores para cualquiera de las magnitudes, direcciones y puntos de aplicación conocidos para los vectores de fuerza y proporcione nombres de variables para cualquier incógnitas (ya sea magnitudes, direcciones o distancias).

A continuación deberá elegir los\(z\) ejes\(x\)\(y\),, y. Estos ejes sí necesitan ser perpendiculares entre sí, pero no necesariamente tienen que ser horizontales o verticales. Si eliges ejes de coordenadas que se alinean con algunos de tus vectores de fuerza simplificarás el análisis posterior.

Una vez que haya elegido los ejes, debe desglosar todos los vectores de fuerza en componentes a lo largo de las\(x\)\(z\) direcciones\(y\) y (consulte la página de vectores en la página del Apéndice 1 para obtener más detalles sobre este proceso). Tu primera ecuación será la suma de las magnitudes de los componentes en la\(x\) dirección siendo igual a cero, la segunda ecuación será la suma de las magnitudes de los componentes en la\(y\) dirección siendo igual a cero, y la tercera (si tienes un problema 3D) será la suma del magnitudes en la\(z\) dirección siendo iguales a cero.

A continuación necesitarás idear las ecuaciones del momento. Para ello necesitarás elegir un punto sobre el que tomarte los momentos. Cualquier punto debería funcionar, pero suele ser ventajoso elegir un punto que disminuya el número de incógnitas en la ecuación. Recuerda que cualquier vector de fuerza que viaje por un punto dado no ejercerá ningún momento sobre ese punto. Para escribir las ecuaciones de momento, simplemente suma los momentos ejercidos por cada fuerza (sumando los momentos puros mostrados en el diagrama) sobre el punto dado y el eje dado, y establecer esa suma igual a cero. Todos los momentos serán sobre el\(z\) eje para problemas bidimensionales, aunque los momentos pueden ser sobre el\(x\),\(y\) y\(z\) ejes para problemas tridimensionales.

Una vez que tengas tus ecuaciones de equilibrio, puedes resolver estas fórmulas para incógnitas. El número de incógnitas por las que podrás resolver volverá a ser el número de ecuaciones que tengas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/OiJ2xbMIixY.

Ejemplo\(\PageIndex{1}\)

El auto de abajo tiene un peso de 1500 lbs con el centro de masa 4 pies detrás de las ruedas delanteras del auto. ¿Cuáles son las fuerzas normales en las ruedas delanteras y traseras del automóvil?

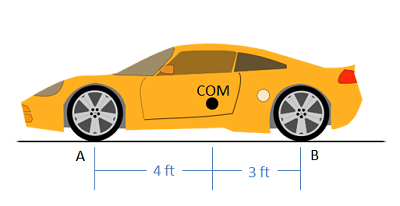
Vista lateral de un automóvil orientado hacia la izquierda, con el centro de masa marcado como 4 pies a la derecha del punto A, la rueda delantera y 3 pies a la izquierda del punto B, la rueda trasera. — Figura\(\PageIndex{1}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Adaptado de la imagen de dominio público por Ebaychatter0.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/1LD5QW-70PA.

Ejemplo\(\PageIndex{2}\)

Una viga de 5 metros de largo tiene una conexión fija a una pared en el punto A y una fuerza que actúa como se muestra en el punto B. ¿Cuáles son las fuerzas de reacción que actúan sobre la viga en el punto A?

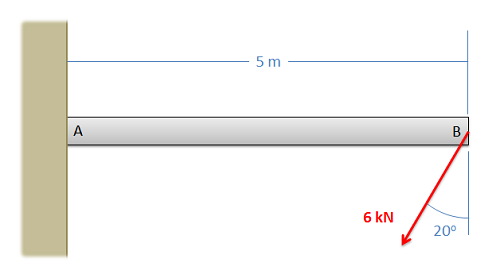
Una viga horizontal de 5 metros de largo tiene su extremo izquierdo, punto A, unido a una pared. En su extremo libre, punto B, se aplica una fuerza de magnitud 6 kN hacia abajo y hacia la izquierda, haciendo un ángulo de 20 grados con la vertical. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Una viga horizontal unida a la pared en un extremo experimenta una fuerza aplicada en su extremo libre.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/JrVV7k1aQEk.

Ejemplo\(\PageIndex{3}\)

Una escalera con una masa insignificante sostiene a una persona de 120 lb como se muestra a continuación. Si el punto de contacto en A no tiene fricción y el punto de contacto en B es una conexión aproximada, determine las fuerzas que actúan en los puntos de contacto A y B.

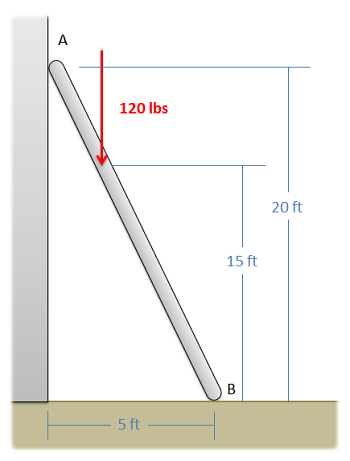
Una escalera está apoyada contra una pared, con su base a 5 pies de distancia de la pared y su parte superior a 20 pies sobre el suelo. Una persona que pesa 120 lbs se para en la escalera en un lugar a 15 pies sobre el suelo. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una escalera con su base sobre un piso rugoso se apoya contra una pared sin fricción, con una persona parada en la escalera a mitad de camino hacia arriba.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/WzkAnPdhao4.

Ejemplo\(\PageIndex{4}\)

El miembro ABC tiene 6 metros de largo, estando el punto B en su punto medio. Determinar todas las fuerzas que actúan sobre el miembro ABC.

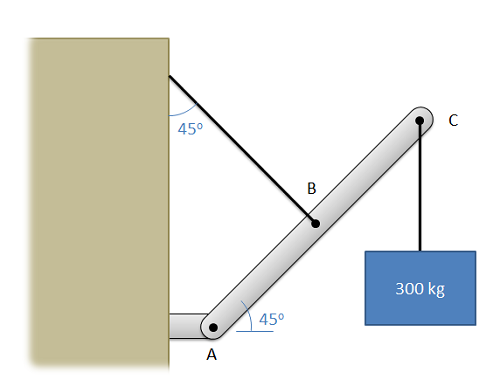
Un miembro estructural consiste en el punto A, la intersección entre una viga horizontal unida a una pared y una viga diagonal de 6 metros de largo en un ángulo de 45 grados por encima de la horizontal; el punto B, el punto medio de la viga diagonal y el punto de unión para un cable fijado a la pared formando un ángulo de 45 grados por debajo del horizontal; y punto C, el extremo libre de la viga diagonal con una carga de 300 kg colgando de ella. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Un miembro estructural diagonal está unido a la pared en un extremo, conectado a la pared a través de un cable en su punto medio y sosteniendo una carga de 300 kg en su extremo libre.

Solución: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/sMQrjwUMpSQ.

Ejemplo\(\PageIndex{5}\)

Mientras está sentada en una silla, una persona ejerce las fuerzas en el siguiente diagrama. Determine todas las fuerzas que actúan sobre la silla en los puntos A y B. (Supongamos que A no tiene fricción y B es una superficie rugosa).

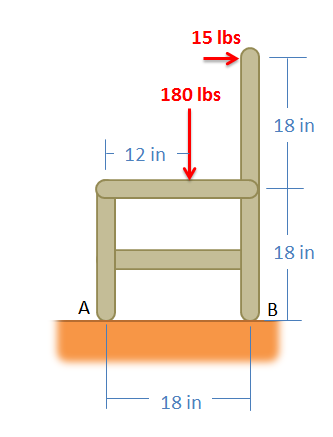
Vista lateral de una silla orientada hacia la izquierda, con un asiento a 18 pulgadas sobre el suelo, el borde superior del respaldo de la silla a 18 pulgadas por encima del asiento y 18 pulgadas entre las piernas izquierda y derecha. Los puntos A y B son los puntos donde las patas izquierda y derecha de la silla tocan el suelo respectivamente. Se ejerce una fuerza hacia abajo de 180 lbs sobre el asiento de la silla, 12 pulgadas detrás del borde delantero del asiento, y una fuerza hacia la derecha de 15 lbs se ejerce contra el borde superior del respaldo del asiento. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{5}\). Una silla se coloca sobre una superficie plana, asumiendo que esa superficie es sin fricción donde entra en contacto con la pata delantera de la silla (punto A) y ejerciendo fricción donde entra en contacto con la pata trasera (punto B).

Solución: Video\(\PageIndex{6}\): Solución trabajada a problema de ejemplo\(\PageIndex{5}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/nSOxK1ZMggA.

Ejemplo\(\PageIndex{6}\)

El tráiler que se muestra a continuación consiste en una plataforma con un peso de 250 lbs sobre un eje con ruedas con un peso de 350 lbs. Supongamos que las fuerzas de peso actúan en el centro de cada componente. Si deseamos que el peso de la lengüeta (\(F_T\)) del remolque descargado sea de 50 lbs, ¿cuál es la distancia\(d\) desde el frente donde debemos colocar el eje?

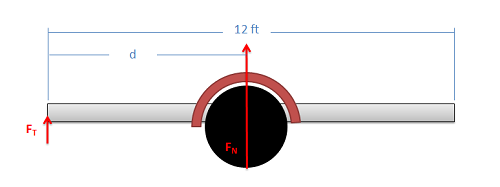
Un remolque que consiste en una plataforma plana rectangular que pesa 250 lbs, soportada sobre 2 ruedas que pesan 350 lbs conectadas por un eje. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{6}\). Un tráiler consiste en una plataforma plana rectangular en la parte superior de dos ruedas sobre un eje.

Solución: Video\(\PageIndex{7}\): Solución trabajada a problema de ejemplo\(\PageIndex{6}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/wpEBuitLD5s.

Ejemplo\(\PageIndex{7}\)

Un letrero plano de acero de 12 pulgadas por 24 pulgadas está soportado por dos cables, cada uno a 6 pulgadas del borde del letrero. El letrero tiene un peso de 10 lbs, y el viento está haciendo que el letrero se asiente en un ángulo de 10 grados con respecto a la vertical (el\(y\) eje). Si tratamos al viento como una fuerza puntual que actúa en\(z\) dirección negativa sobre el centro del letrero, ¿qué tan fuerte debe ser la fuerza del viento para provocar este ángulo de diez grados?

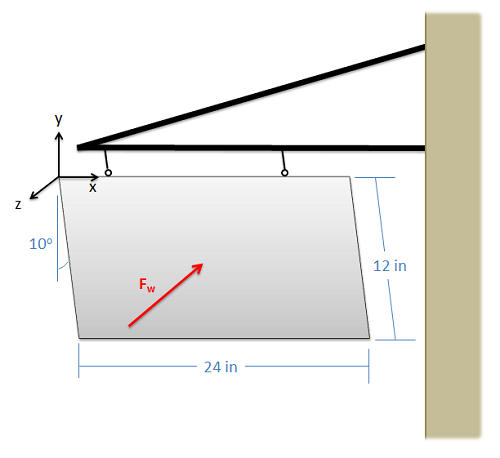
Un letrero rectangular de metal de 10 lb, de 12 por 24 pulgadas, está colgado con su lado más largo horizontal. Está soportado desde la parte superior por 2 cables, cada uno unido a 6 pulgadas de un borde del letrero. Un viento empuja el letrero hacia la pantalla, por lo que hace un ángulo de 10 grados con el plano de la pantalla. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{7}\). Un letrero colgante experimenta un viento cuya dirección apunta hacia la pantalla, lo que hace que el letrero forme un ángulo de 10° con el plano de la pantalla.

Solución: Video\(\PageIndex{8}\): Solución trabajada a problema de ejemplo\(\PageIndex{7}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/pR-0xbj8wF0.

Ejemplo\(\PageIndex{8}\)

Un panel acústico de sesenta kilogramos está suspendido por tres cables como se muestra a continuación. Suponiendo que el panel tiene un peso distribuido uniformemente, ¿cuál es la tensión en cada uno de los cables?

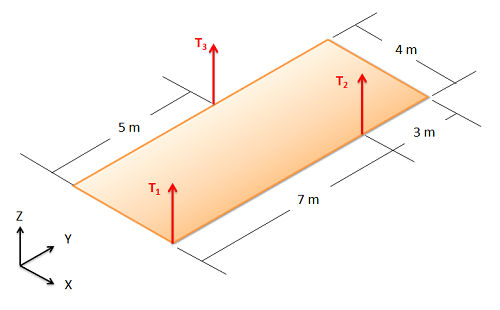
Un panel rectangular de 60 kg, de dimensiones 10 por 4 metros con un lado más corto orientado hacia el espectador, se encuentra en el plano xy (en el plano del piso). Está suspendido del techo por 3 cables: cable 1 en la esquina delantera derecha, cable 2 7 metros detrás de la ubicación del cable 1, y cable 3 en el punto medio del lado izquierdo del panel. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{8}\). Un panel rectangular uniforme está suspendido desde arriba por 3 cables ubicados en diferentes puntos a lo largo de sus bordes.

Solución: Video\(\PageIndex{9}\): Solución trabajada a problema de ejemplo\(\PageIndex{8}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/Kbsc1m0f9pQ.