4.5: Carga puntual equivalente

Última actualización
Guardar como PDF

Page ID: 84092

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Una carga puntual equivalente es una fuerza de punto único que tendrá el mismo efecto en un cuerpo que la condición de carga original, que generalmente es una fuerza distribuida. La carga puntual equivalente siempre debe causar la misma aceleración lineal y aceleración angular que la fuerza original a la que es equivalente (o causar las mismas fuerzas de reacción si el cuerpo está restringido). Encontrar la carga puntual equivalente para una fuerza distribuida a menudo ayuda a simplificar el análisis de un sistema al eliminar las integrales de las ecuaciones de equilibrio o ecuaciones de movimiento en análisis posteriores.

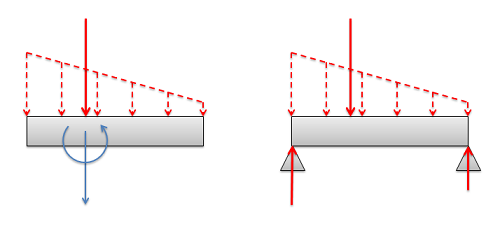
A la izquierda, se muestra un cuerpo rectangular experimentando una carga de punto descendente (dibujado como un vector sólido) equivalente a una carga distribuida sobre su borde superior (dibujado como una serie de vectores discontinuos), lo que hace que el cuerpo experimente aceleración lineal hacia abajo y aceleración rotacional en sentido contrario a las agujas del reloj. A la derecha, el mismo cuerpo que experimenta la misma fuerza distribuida ahora está constreñido por un soporte en los extremos inferior izquierdo y derecho, equilibrándose la fuerza puntual equivalente hacia abajo por las fuerzas normales hacia arriba ejercidas por los soportes. — Figura\(\PageIndex{1}\): Si el cuerpo no está restringido como se muestra a la izquierda, la carga puntual equivalente (mostrada como un vector sólido) provocará la misma aceleración lineal y angular que la carga distribuida original (mostrada con vectores discontinuos). Si el cuerpo está restringido como se muestra a la derecha, la carga puntual equivalente (mostrada como un vector sólido) provocará las mismas fuerzas de reacción que la fuerza distribuida original (mostrada con vectores discontinuas).

Búsqueda de la carga puntual equivalente

Al encontrar la carga puntual equivalente, necesitamos encontrar la magnitud, dirección y punto de aplicación de una sola fuerza que sea equivalente a la fuerza distribuida que se nos da. En este curso solo trataremos con fuerzas distribuidas con una dirección uniforme, en cuyo caso la dirección de la carga puntual equivalente coincidirá con la dirección uniforme de la fuerza distribuida. Esto deja por encontrar la magnitud y el punto de aplicación. Hay dos opciones disponibles para encontrar estos valores:

Podemos encontrar la magnitud y el punto de aplicación de la carga puntual equivalente a través de la integración de las funciones de fuerza.
Podemos utilizar el área/volumen y el centroide/centro de volumen del área o volumen bajo la función de fuerza.

El primer método es más flexible, lo que nos permite encontrar la carga puntual equivalente para cualquier función de fuerza para la que podamos hacer una fórmula matemática (asumiendo que tenemos la habilidad en cálculo para integrar esa función). El segundo método suele ser más rápido, suponiendo que podemos buscar los valores para el área o volumen bajo la curva de fuerza y los valores para el centroide o centro de volumen para el área bajo la curva.

Uso de la integración en problemas de fuerza superficial 2D:

Figura\(\PageIndex{2}\): El bloque mostrado arriba tiene una fuerza distribuida que actúa sobre él. La función de fuerza relaciona la magnitud de la fuerza con la\(x\) posición a lo largo de la parte superior de la caja.

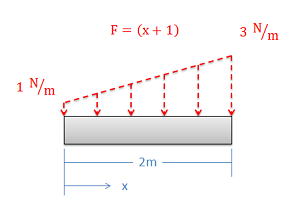
Un cuerpo rectangular de dos metros de largo se coloca en un eje x, con el extremo izquierdo correspondiente a x=0 y la dirección x positiva está a la derecha. El cuerpo experimenta una fuerza distribuida hacia abajo a lo largo de su borde superior, variando en magnitud desde un valor de 1 N/m en el extremo izquierdo hasta 3 N/m en el extremo derecho, descrito por la función de fuerza F=x+1. — Figura\(\PageIndex{2}\): El bloque mostrado arriba tiene una fuerza distribuida que actúa sobre él. La función de fuerza relaciona la magnitud de la fuerza con la\(x\) posición a lo largo de la parte superior de la caja.

Encontrar la carga puntual equivalente a través de la integración siempre comienza determinando la fórmula matemática que es la función de fuerza. La función de fuerza relaciona matemáticamente la magnitud de la fuerza\((F)\) con la posición\((x)\). En este caso la fuerza está actuando a lo largo de una sola línea, por lo que la posición puede determinarse en su totalidad conociendo la\(x\) coordenada, pero en problemas posteriores también podemos necesitar relacionar la magnitud de la fuerza con las\(z\) coordenadas\(y\) y. En nuestro ejemplo anterior, podemos relacionar la magnitud de la fuerza con la posición al afirmar que la magnitud de la fuerza en cualquier punto en Newtons por metro es igual a la\(x\) posición en metros más uno.

La magnitud de la carga puntual equivalente será igual al área bajo la función de fuerza. Esta será la integral de la función de fuerza en toda su longitud (en este caso, de\(x = 0\) a\(x = 2\)).

\[ F_{eq} = \int\limits_{x \, min}^{x \, max} F(x) \, dx \]

Ahora que tenemos la magnitud de la carga puntual equivalente de tal manera que coincida con la magnitud de la fuerza original, necesitamos ajustar la posición de\((x_{eq})\) tal manera que provoque el mismo momento que la fuerza distribuida original. El momento de la fuerza distribuida será la integral de la función de fuerza\((F(x))\) multiplicada por el momento brazo sobre el origen\((x)\). El momento de la carga puntual equivalente será igual a la magnitud de la carga puntual equivalente que acabamos de encontrar multiplicada por el brazo de momento para la carga puntual equivalente\((x_{eq})\). Si establecemos estas dos cosas iguales entre sí y luego resolvemos para la posición de la carga puntual equivalente nos\((x_{eq})\) quedamos con la siguiente ecuación.

\[ x_{eq} = \frac{\int\limits_{x \, min}^{x \, max} (F(x) * x) \, dx}{F_{eq}} \]

Ahora que tenemos la magnitud, dirección y posición de la carga puntual equivalente, podemos dibujar la carga puntual en nuestro diagrama original. Esta fuerza puntual se puede utilizar en lugar de la fuerza distribuida en análisis posteriores.

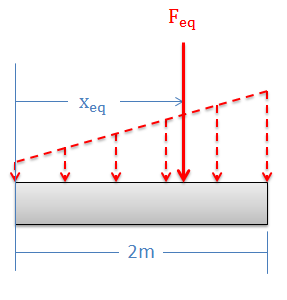
El mismo rectángulo que experimenta una fuerza distribuida a lo largo de su borde superior, representado por vectores discontinuos, de la Figura 4.5.2 se representa experimentando una carga puntual equivalente a esa fuerza distribuida, representada en un vector sólido, en la ubicación x_eq desde su borde izquierdo. — Figura\(\PageIndex{3}\): Los valores para\(F_{eq}\) y para los\(x_{eq}\) que hemos resuelto son la magnitud y posición de la carga puntual equivalente.

Uso del Área y Centroide en Problemas de Fuerza de Superficie 2D:

Como alternativa al uso de la integración, podemos usar el área bajo la curva de fuerza y el centroide del área bajo la curva de fuerza para encontrar la magnitud de la carga puntual equivalente y el punto de aplicación respectivamente.

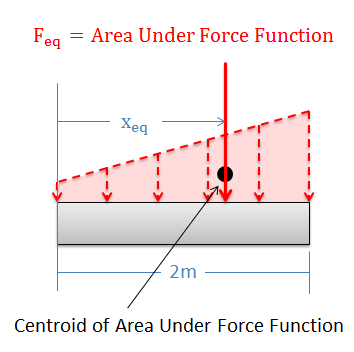
Un cuerpo rectangular de 2 metros de largo experimenta una fuerza distribuida hacia abajo, representada por una serie de vectores discontinuas, a lo largo de su borde superior. El área dentro del límite de los vectores punteados pero por encima del borde superior del rectángulo está sombreada. Se marca el centroide de esta región sombreada, pasando por este punto la carga puntual equivalente (representada por un vector sólido). El centroide es una distancia de x_eq metros desde el extremo izquierdo del rectángulo. — Figura\(\PageIndex{4}\): La magnitud de la carga puntual equivalente es igual al área bajo la función de fuerza. Además, la carga puntual equivalente viajará a través del centroide del área bajo la función de fuerza.

La magnitud\((F_{eq})\) de la carga puntual equivalente será igual al área bajo la función de fuerza. Podemos encontrar esta área usando cálculo, pero a menudo hay formas más fáciles basadas en la geometría de encontrar el área bajo la función de fuerza.

La carga puntual equivalente también viajará a través del centroide del área bajo la función de fuerza. Esto nos permite encontrar el valor para\(x_{eq}\). El centroide para muchas formas comunes se puede buscar en tablas, y el teorema del eje paralelo se puede usar para determinar el centroide de formas más complejas (consulte la página del Apéndice sobre centroides para más detalles).

Uso de la integración en problemas de fuerza superficial 3D:

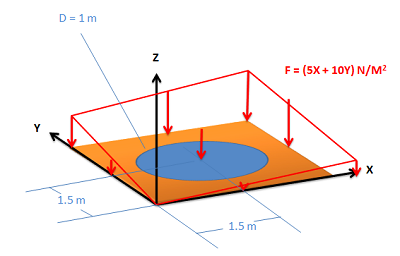
Un prisma rectangular se ubica con una esquina en el origen de un sistema de coordenadas 3D, su cara superior alineada a lo largo de los ejes del primer cuadrante del plano XY y su altura alineada a lo largo del eje z. La cara superior experimenta una fuerza distribuida hacia abajo, descrita con la función de fuerza F= (5x+10y) Newtons por metro cuadrado. — Figura\(\PageIndex{5}\): La magnitud de la fuerza superficial en este ejemplo varía con ambos\(x\) y\(y\).

Con la fuerza superficial en un problema 3D, la fuerza se distribuye sobre una superficie, en lugar de a lo largo de una sola línea. Para encontrar la magnitud de la carga puntual equivalente comenzaremos nuevamente por encontrar la ecuación matemática para la función de fuerza. Debido a que la fuerza se distribuye sobre un área en lugar de solo una línea, la magnitud de la fuerza puede estar relacionada tanto con la\(x\) coordenada como con la\(y\) coordenada, en lugar de solo la\(x\) coordenada como antes.

La magnitud de la carga puntual equivalente\((F_{eq})\) será igual al volumen bajo la curva de fuerza. Para calcular este valor integraremos la función de fuerza sobre el área a la que se aplica la fuerza. Para integrar esta función\(F(x,y)\) en términos del área, tendremos que desglosar aún más la integral, integrándonos una\(x\) y luego integrando sobre\(y\).

\[ F_{eq} = \int F(x,y) \, dA = \int\limits_{y \, min}^{y \, max} \left( \, \int\limits_{x \, min}^{x \, max} F(x,y) \, dx \right) \, dy \]

Una vez que resolvemos la magnitud de la carga puntual equivalente, entonces podemos resolver para la posición de la carga puntual equivalente. Dado que la fuerza se extiende sobre una superficie, necesitaremos calcular tanto las coordenadas como\(x\)\((x_{eq})\) las\(y\)\((y_{eq})\) coordenadas para la posición. El proceso para resolver estos valores es similar a lo que se hizo con solo un\(x\) valor, excepto que cambiamos el valor del brazo de momento para que coincida con la coordenada de carga puntual equivalente que estamos buscando.

\[ x_{eq} = \frac{\int (F(x,y) * x) \, dA}{F_{eq}} \]

\[ y_{eq} = \frac{\int (F(x,y) * x) \, dA}{F_{eq}} \]

En cada una de las ecuaciones anteriores, necesitaremos expandir el área integral en\(x\)\(y\) e integrales (como hicimos para\(F_{eq}\)) para poder resolverlas.

Uso de Volumen y Centro de Volumen en Problemas de Fuerza de Superficie 3D:

Al igual que en los problemas 2D, hay algunos atajos disponibles para encontrar la carga puntual equivalente en problemas de fuerza superficial 3D. Para una fuerza extendida sobre un área, la magnitud\((F_{eq})\) de la carga puntual equivalente será igual al volumen bajo la función de fuerza. La carga puntual equivalente también viajará por el centro de volumen del volumen bajo la función de fuerza. Esto debería permitirle determinar ambos\(x_{eq}\) y\(y_{eq}\).

El centro de volumen de una forma será el mismo que el centro de masa de una forma si se supone que la forma tiene una densidad uniforme. Debería ser posible buscar estos valores en busca de formas comunes en una tabla. Nuevamente, el teorema del eje paralelo se puede utilizar para encontrar el centro del volumen para formas más complejas (Ver la página Centro de Masa en el Apéndice 2 para más detalles).

Uso de la Integración en Problemas de Fuerza Corporal:

Cuando saltamos a las fuerzas del cuerpo, la magnitud de nuestra fuerza variará con\(x\)\(y\), y\(z\) coordina. Esto significa que nuestra función de fuerza puede incluir todas estas variables\((F(x,y,z))\). Para encontrar la magnitud de la carga puntual equivalente, integramos sobre el volumen, dividiendo la integral del volumen en\(x\)\(y\), y luego\(z\) integrales.

\ begin {align} F_ {eq} &=\ int F (x, y, z)\, dV\\ &=\ int\ limits_ {z\, min} ^ {z\, max}\ left (\,\ int\ límites_ {y\, min} ^ {y\, max}\ left (\,\ int\ límites_ {x\, min} ^ {x\, max} F (x, y, z)\, dx\ derecha)\, dy\ derecha)\, dz\ end {align}

Para encontrar el punto de aplicación de la carga puntual equivalente, necesitaremos encontrar las tres posiciones de coordenadas. Para ello, ampliaremos las ecuaciones que usamos con dos coordenadas para incluir la tercera coordenada\((z_{eq})\).

\[ x_{eq} = \frac{\int (F(x,y,z) * x) \, dV}{F_{eq}} \]

\[ y_{eq} = \frac{\int (F(x,y,z) * y) \, dV}{F_{eq}} \]

\[ z_{eq} = \frac{\int (F(x,y,z) * z) \, dV}{F_{eq}} \]

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/eikERyUNIOo.

Ejemplo\(\PageIndex{1}\)

Determinar la magnitud y el punto de aplicación para la carga puntual equivalente de la fuerza distribuida que se muestra a continuación.

Una barra horizontal de 10 metros de largo está unida a una pared en su extremo izquierdo. Comenzando en el punto a 3 metros de distancia de la pared, experimenta una fuerza distribuida hacia abajo que varía linealmente desde magnitud 14 kN/m hasta magnitud 0 en el extremo derecho de la barra. — Figura\(\PageIndex{6}\): diagrama de problemas por ejemplo\(\PageIndex{1}\); una barra unida a un muro experimenta una fuerza distribuida cuya magnitud varía linealmente en parte de su longitud.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/h_E0XjIJaiI.

Ejemplo\(\PageIndex{2}\)

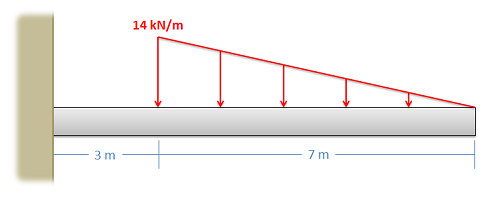
Determinar la magnitud y el punto de aplicación para la carga puntual equivalente de la fuerza distribuida que se muestra a continuación.

Una barra horizontal de 3 pies de largo está unida a una pared en su extremo derecho. Se experimenta una fuerza distribuida hacia abajo en toda su longitud, cuya magnitud varía cuadráticamente de 1800 libras/pie en el extremo izquierdo de la barra a 0 en el extremo derecho. — Figura\(\PageIndex{7}\): diagrama de problemas por ejemplo\(\PageIndex{2}\); una barra unida a un muro experimenta una fuerza distribuida cuya magnitud varía cuadráticamente a lo largo de su longitud.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/D4JoQpOyI38.

Ejemplo\(\PageIndex{3}\)

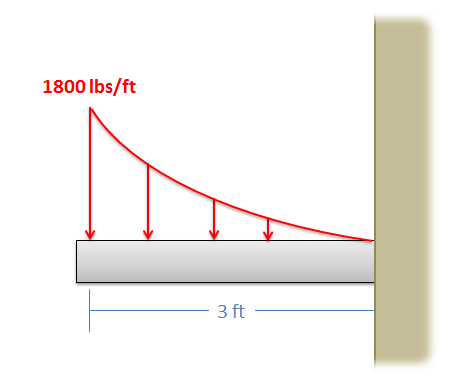
Determinar la magnitud y el punto de aplicación para la carga puntual equivalente de la fuerza distribuida que se muestra a continuación.

Una barra horizontal de 10 metros de largo está unida a una pared en su extremo izquierdo. Experimenta una fuerza distribuida hacia abajo cuya magnitud varía linealmente de 0 en el extremo izquierdo a 10 kN/m a mitad de la longitud de la barra, permaneciendo constante a 10 kN/m para los 5 metros más a la derecha de la barra. — Figura\(\PageIndex{8}\): diagrama de problemas por Ejemplo\(\PageIndex{3}\); una barra unida a una pared experimenta una fuerza distribuida cuya magnitud varía linealmente en parte de su longitud y permanece constante por el resto.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/UbnfNAQctyg.

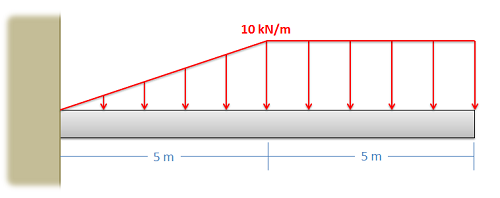
Ejemplo\(\PageIndex{4}\)

El viento ha amontonado arena en una esquina de un edificio. El supervisor del edificio está preocupado por el peso de la arena empujando contra el techo del sótano de abajo. La función que describe la fuerza de la arena que empuja hacia abajo sobre la superficie se da a continuación. Encuentra la magnitud, dirección y punto de aplicación de la carga puntual equivalente para la fuerza distribuida de la arena. Dibuje la carga puntual equivalente en un diagrama.

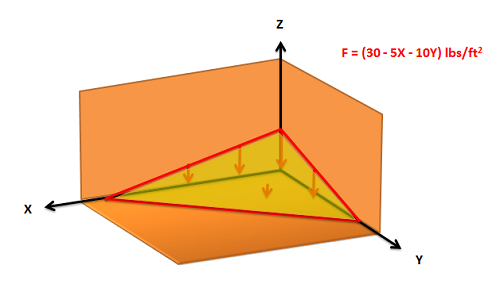
Un sistema de coordenadas tridimensional con el plano XY que indica el suelo. Una esquina de la “caja” formada por el primer cuadrante está sombreada, con vectores que representan una fuerza distribuida que empuja hacia abajo contra el plano XY. La magnitud de la fuerza distribuida se describe con la ecuación F = (30-5x-10y) lbs por pie cúbico. — Figura\(\PageIndex{9}\): diagrama de problemas por Ejemplo\(\PageIndex{4}\); la arena acumulada en la esquina de un edificio se asigna a un sistema de coordenadas tridimensional y la fuerza distribuida que ejerce sobre el piso debajo de él se describe con una ecuación de fuerza.

Solución: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/IaSe_g3_Mgk.