7.3: Cinemática bidimensional con coordenadas rectangulares
- Page ID
- 83919
El movimiento bidimensional (también llamado movimiento plano) es cualquier movimiento en el que los objetos que se analizan permanecen en un solo plano. Al analizar dicho movimiento, primero debemos decidir el tipo de sistema de coordenadas que deseamos utilizar. Las opciones más comunes en ingeniería son los sistemas de coordenadas rectangulares, los sistemas de coordenadas normal-tangenciales y los sistemas de coordenadas polares. Cualquier movimiento plano puede describirse potencialmente con cualquiera de los tres sistemas, aunque cada elección tiene ventajas y desventajas potenciales.
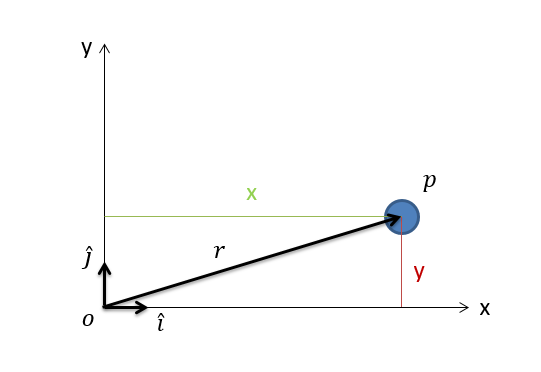
El sistema de coordenadas rectangulares (también llamado a veces sistema de coordenadas cartesianas) es el enfoque más intuitivo para describir el movimiento. En los sistemas de coordenadas rectangulares tenemos un\(x\) eje -eje y un\(y\) -eje. Estos ejes permanecen fijos a algún punto de origen en el entorno y no cambian con el tiempo. En cambio, los cuerpos que estamos analizando suelen moverse con relación a estos ejes fijos. Un ejemplo de un cuerpo con un sistema de coordenadas rectangulares se muestra en la siguiente figura.
Las coordenadas rectangulares funcionan mejor para sistemas donde todas las fuerzas mantienen una dirección constante. El ejemplo más común de esto es el movimiento del proyectil, donde la gravedad (la única fuerza en estos sistemas) mantiene una dirección descendente constante. Un ejemplo de un sistema donde las fuerzas cambian de dirección con el tiempo sería algo así como un automóvil dando la vuelta a una curva en la carretera. En este caso, la fuerza de fricción en las llantas va a estar rotando con el auto. Por lo tanto, el problema del automóvil será más adecuado para el uso de sistemas de coordenadas normal-tangenciales o polares.
Al describir la posición de un punto en sistemas de coordenadas rectangulares, vamos a comenzar describiendo ambas\(x\) y\(y\) coordenadas en forma vectorial. Para ello, los valores\(x\) y\(y\) representan distancias y los vectores unitarios\(\hat{i}\) y se\(\hat{j}\) utilizan para indicar qué distancia corresponde con qué dirección. Esto puede parecer redundante, pero recuerde a la hora de resolver problemas reales,\(x\) y solo\(y\) serán números.
\[ \text{Position:} \quad r_{p/o} (t) = x(t) \ \hat{i} + y(t) \ \hat{j} \]
Al igual que con los problemas unidimensionales, si tomamos la derivada de la ecuación de posición, encontraremos la ecuación de velocidad. Si tomamos la derivada de la ecuación de velocidad terminaremos con la ecuación de aceleración. También como problemas unidimensionales, podemos usar la integración para movernos en la otra dirección, pasando de una ecuación de aceleración a una ecuación de velocidad a una ecuación de posición.
Los vectores unitarios agregan un nuevo elemento en dos dimensiones, pero como los vectores unitarios no cambian con el tiempo (son constantes), los tratamos como lo haríamos con cualquier otra constante para derivadas e integrales. Las ecuaciones de velocidad y aceleración resultantes son las siguientes.
\ begin {align}\ text {Velocidad:}\ quad &\, v (t) =\ punto {x} (t)\\ hat {i} +\ punto {y} (t)\\ hat {j}\\ [5pt]\ text {Aceleración:}\ quad &\, a (t) =\ ddot {x} (t)\\ hat {i} +\ ddot {y} (t)\\ hat {j}\ end {align}
Las ecuaciones anteriores son ecuaciones vectoriales con velocidades y aceleraciones divididas en\(x\) y\(y\) componentes. Dado que las\(y\) direcciones\(x\) y son perpendiculares, también son independientes (el movimiento en la\(x\) dirección no impacta en el movimiento en la\(y\) dirección, y viceversa). Esto esencialmente significa que podemos dividir nuestra ecuación vectorial en un conjunto de dos ecuaciones escalares. Para ello solo ponemos todo delante de los vectores\(\hat{i}\) unitarios en las\(x\) ecuaciones y todo delante de los vectores\(\hat{j}\) unitarios en las\(y\) ecuaciones.
\ begin {align}\ text {Posición:}\ quad &\, x (t) =\ dots\ quad\ quad y (t) =\ puntos\\ [5pt]\ text {Velocidad:}\ quad &\,\ punto {x} (t) =\ puntos\ quad\ quad\ punto {y} (t) =\ puntos\ [5pt]\ texto {Aceleración:}\ quad y\,\ ddot {x} (t) =\ puntos\ quad\ quad\ ddot {y} (t) =\ puntos\ final {alinear}
Una vez que tenemos todo dividido en\(x\) ecuaciones\(y\) de dirección y dirección, podemos usar los mismos procesos que usamos para el movimiento unidimensional para pasar de\(x\)\(\dot{x}\) a\(\ddot{x}\), y de\(y\) a\(\dot{y}\) a\(\ddot{y}\). La variable que une las dos ecuaciones es el tiempo\((t)\).
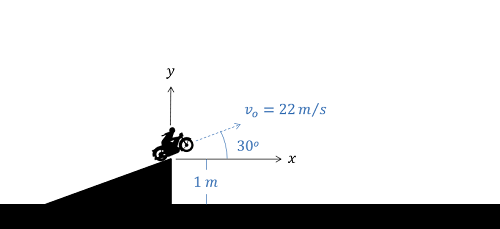
Una motocicleta sale de una rampa de un metro de altura en un ángulo de 30 grados como se muestra a continuación. Determinar las ecuaciones para la aceleración, velocidad y posición a lo largo del tiempo. ¿A qué distancia recorre la motocicleta en\(x\) dirección antes de chocar contra el suelo?
- Solución
-
Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/ujM4LIQlG1Q.
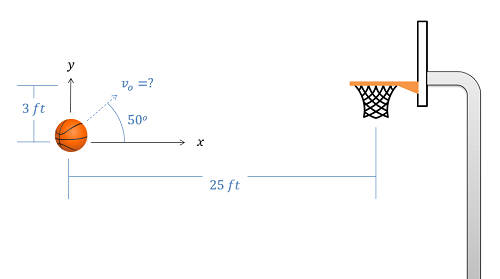
Se lanza una básquetbol hacia un aro que está tres pies más alto en la\(y\) dirección y 25 pies de distancia en la\(x\) dirección. Si la pelota se lanza en un ángulo inicial de 50 grados, ¿cuál debe ser la velocidad inicial para que la pelota llegue al aro?
- Solución
-
Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/IGBB1YXRNr0.


