7.4: Cinemática Bidimensional con Coordenadas Normal-Tangenciales

Última actualización
Guardar como PDF

Page ID: 83934

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El movimiento bidimensional (también llamado movimiento plano) es cualquier movimiento en el que los objetos que se analizan permanecen en un solo plano. Al analizar dicho movimiento, primero debemos decidir el tipo de sistema de coordenadas que deseamos utilizar. Las opciones más comunes en ingeniería son los sistemas de coordenadas rectangulares, los sistemas de coordenadas normal-tangenciales y los sistemas de coordenadas polares. Cualquier movimiento plano puede describirse potencialmente con cualquiera de los tres sistemas, aunque cada elección tiene ventajas y desventajas potenciales.

El sistema de coordenadas normal-tangencial se centra en el cuerpo en movimiento. El punto de origen será el propio cuerpo, lo que significa que la posición de la partícula en el sistema de coordenadas normal-tangencial es siempre “cero”. La dirección tangencial (\(t\)-dirección) se define como la dirección de desplazamiento en ese momento en el tiempo (la dirección del vector de velocidad actual), siendo la dirección normal (\(n\)-dirección) 90 grados en sentido antihorario desde la\(t\) dirección -dirección. El siguiente diagrama muestra una partícula siguiendo una trayectoria curva con las direcciones normales y tangenciales actuales.

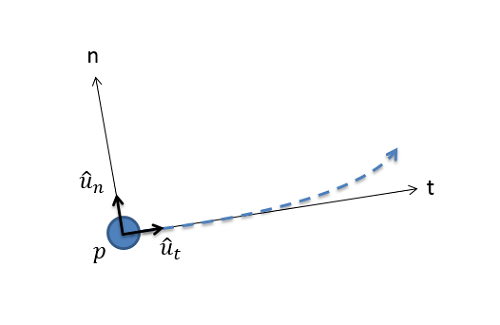
Una partícula que viaja a lo largo de un camino que se curva hacia arriba y hacia la derecha. En el instante actual, está en la posición p y su dirección tangencial apunta hacia la derecha y ligeramente hacia arriba, tangente a la trayectoria en el punto p. Su dirección normal es de 90 grados en sentido antihorario a la dirección tangencial. — Figura\(\PageIndex{1}\): En el sistema de coordenadas normal-tangencial, la propia partícula sirve como punto de origen. La\(t\) dirección -es la dirección actual de desplazamiento y la\(n\) dirección -siempre es 90° en sentido contrario a las agujas del reloj desde la\(t\) dirección -dirección. \(\hat{u}_n\)Los vectores\(\hat{u}_t\) y representan vectores unitarios en las\(n\) direcciones\(t\) y respectivamente.

Los sistemas de coordenadas normal-tangenciales funcionan mejor cuando observamos el movimiento desde la perspectiva del cuerpo en movimiento, como ser un pasajero en un automóvil o avión. En tales casos, nos definiríamos como el punto de origen y “hacia adelante” sería la dirección tangencial. Una distinción importante entre el sistema de coordenadas rectangulares y el sistema de coordenadas normal-tangencial es que los ejes no están fijos en el sistema de coordenadas normal-tangencial. Si volvemos al ejemplo del automóvil, la dirección “hacia adelante” o tangencial girará con el automóvil, pero la dirección “este” o la dirección\(x\) -dirección permanecerán constantes sin importar en qué dirección apunte el automóvil.

La forma en que se define el sistema de coordenadas, la posición de la partícula siempre se establece para que esté en el punto de origen. La velocidad también se establece siempre para estar en la dirección tangencial, y por lo tanto no hay velocidad en la\(n\) dirección -dirección. La variable\(v\) es la velocidad actual del cuerpo.

\ begin {align}\ text {Posición:}\ quad &\, r_ {p/o} (t) = 0\\ hat {u} _t + 0\\ hat {u} _n\\ [5pt]\ text {Velocidad:}\ quad &\, v (t) = v\\ hat {u} _t\ end {align}

Para encontrar la aceleración, necesitamos tomar la derivada de la función de velocidad. Esto puede parecer sencillo, pero hay algo nuevo a considerar en que el vector\(u_t\) unitario no es constante. Esto significa que un cambio en la velocidad puede provocar una aceleración, y un cambio de dirección (que cambiaría la\(u_t\) dirección) también puede causar una aceleración. Volviendo al ejemplo de nuestro auto, esto tiene cierto sentido intuitivo. Podemos sentir aceleraciones, y podríamos sentir aceleración si de repente pisamos el acelerador y aumentáramos nuestra velocidad, pero también podríamos sentir la aceleración si damos un giro apretado a una velocidad constante.

Volviendo a la derivada, utilizaremos la regla del producto, tomando la derivada de una pieza a la vez.

\[ \text{Acceleration:} \quad \, a(t) = \dot{v} \hat{u}_t + v \dot{\hat{u}}_t \]

\(\dot{v}\)es la tasa de cambio de velocidad del cuerpo, que se llama la aceleración tangencial. Volviendo a nuestra analogía de autos, esta es la aceleración que experimentaríamos al presionar los pedales de gasolina o freno.

La otra pieza de nuestra derivada es la velocidad multiplicada por la derivada de un vector unitario, que necesitaremos analizar más a fondo. Al pensar en la derivada de un vector unitario giratorio, pensamos en rotar el sistema de coordenadas en una pequeña cantidad\(d \theta\).

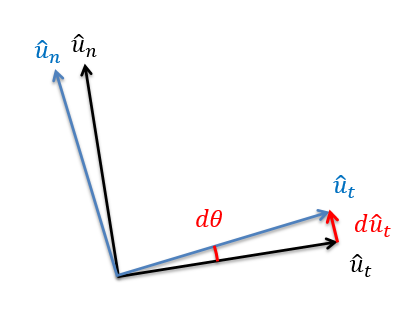
Los vectores unitarios normal-tangenciales de una partícula a medida que gira en sentido antihorario en una pequeña cantidad d theta. El vector d u-hat_t apunta desde la cabeza del vector u-hat_t anterior a la rotación hasta la cabeza del vector u-hat_t desde después de la rotación. — Figura\(\PageIndex{2}\): La derivada de un vector unitario giratorio puede pensarse como el cambio en la posición de la cabeza de ese vector a medida que gira alrededor de un ángulo pequeño\(d \theta\).

La derivada del\(\hat{u}_t\) vector es entonces el cambio de posición de la cabeza del vector. Usando alguna geometría, podemos ver que la distancia que mueve la cabeza del vector es la longitud del vector (que siempre es 1 para un vector unitario) multiplicada por el ángulo de rotación en radianes. La dirección que recorre la cabeza del\(\hat{u}_t\) vector es aproximadamente la\(\hat{u}_n\) dirección. De hecho, a medida que se\(d \theta\) acerca a cero, se convierte exactamente en la\(\hat{u}_n\) dirección. Volviendo a poner esto en nuestra derivada, terminamos con la siguiente ecuación para la aceleración.

\[ a(t) = \dot{v} \hat{u}_t + v \dot{\hat{u}}_t = \dot{v} \hat{u}_t + v \dot{\theta} \hat{u}_n \]

Antes de llegar a nuestro conjunto final de ecuaciones, tenemos una última sustitución potencial. Si una partícula se mueve a lo largo de una trayectoria curva, la velocidad a la que gira\((\dot{\theta})\) será igual a la velocidad de la partícula dividida por el radio de la trayectoria en ese punto (\(v\)dividida por rho,\(\rho\)). Al poner esta última sustitución, tenemos nuestro conjunto final de ecuaciones con dos opciones equivalentes para calcular las aceleraciones.

\[ a(t) = \dot{v} \hat{u}_t + v \dot{\theta} \hat{u}_n = \dot{v} \hat{u}_t + \frac{v^2}{\rho} \hat{u}_n \]

Al usar estas ecuaciones, es importante recordar que son ecuaciones de aceleración. Si queremos conocer la aceleración general necesitaríamos agregar los dos componentes de aceleración como vectores. Además, si se nos da una aceleración que no está en la dirección normal o tangencial, primero tendremos que romper ese vector de aceleración en componentes normales y tangenciales antes de usar las ecuaciones anteriores. Finalmente, si queremos la velocidad o aceleración en direcciones distintas de las direcciones normal y tangencial, necesitaremos usar una transformación de coordenadas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/TIjJLcmtaq8.

Ejemplo\(\PageIndex{1}\)

Un avión comercial viaja a 250 m/s constantes cuando ejecuta un giro de emergencia de 180 grados. Si el giro dura 20 segundos, ¿cuál es la aceleración que experimentan los pasajeros? ¿Cuál es el radio de la curva tomada por el avión?

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/1cQ-LQC8Ahg.

Ejemplo\(\PageIndex{2}\)

Suponiendo que un intercambio de hoja de trébol tiene un radio de curvatura de 80 metros en la parte más estrecha del giro, ¿qué es lo más rápido que un automóvil podría recorrer alrededor de esta curva sin experimentar más de la mitad de una\(g\) aceleración? Supongamos que el automóvil viaja a una velocidad constante. Si en cambio el automóvil estuviera aumentando la velocidad a una tasa de ^{2 m/s 2}, ¿cuál sería la nueva magnitud general de la aceleración que experimentan los pasajeros?

Un intercambio de hoja de trébol en una autopista, siendo transitado por una serie de autos. — Figura\(\PageIndex{3}\): Un intercambio de hoja de trébol en una carretera.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/_Df_HZU0yHk.