7.5: Movimiento bidimensional con coordenadas polares

Última actualización
Guardar como PDF

Page ID: 83945

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El movimiento bidimensional (también llamado movimiento plano) es cualquier movimiento en el que los objetos que se analizan permanecen en un solo plano. Al analizar dicho movimiento, primero debemos decidir el tipo de sistema de coordenadas que deseamos utilizar. Las opciones más comunes en ingeniería son los sistemas de coordenadas rectangulares, los sistemas de coordenadas normal-tangenciales y los sistemas de coordenadas polares. Cualquier movimiento plano puede describirse potencialmente con cualquiera de los tres sistemas, aunque cada elección tiene ventajas y desventajas potenciales.

El sistema de coordenadas polares utiliza una distancia\((r)\) y un ángulo\((\theta)\) para ubicar una partícula en el espacio. El punto de origen será un punto fijo en el espacio, pero el\(r\) eje -eje del sistema de coordenadas girará para que siempre apunte hacia el cuerpo en el sistema. La variable también\(r\) se utiliza para indicar la distancia desde el punto de origen hasta la partícula. El eje theta será entonces 90 grados en sentido antihorario desde el\(r\) eje -con la variable\(\theta\) que se utilizará para mostrar el ángulo entre el\(r\) eje y algún eje fijo que no gira. El siguiente diagrama muestra una partícula con un sistema de coordenadas polares.

Una partícula se encuentra en el primer cuadrante de un plano cartesiano, con el vector r apuntando desde el origen a su posición y formando un ángulo de theta con el eje x. En el origen, un vector unitario u-hat_r apunta en la dirección del vector r, y el vector u-hat_theta apunta 90 grados en sentido antihorario desde u-hat_r. — Figura\(\PageIndex{1}\): En el sistema de coordenadas polares, la\(r\) dirección siempre apunta desde el punto de origen hasta el cuerpo. La variable también\(r\) se utiliza para indicar la distancia entre los dos puntos. La dirección theta siempre será 90° en sentido contrario a las agujas del reloj desde la\(r\) dirección. Theta también se usa para indicar el ángulo entre la\(r\) dirección y algunos ejes fijos utilizados como referencia. \(\hat{u}_{\theta}\)Los vectores\(\hat{u}_r\) y representan vectores unitarios en las\(\theta\) direcciones\(r\) y, respectivamente.

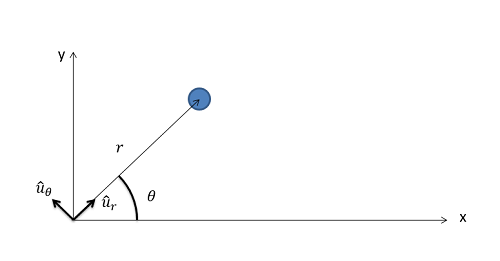
Los sistemas de coordenadas polares funcionan mejor en sistemas donde un cuerpo está siendo rastreado a través de una distancia y un ángulo, como un sistema de radar que rastrea un avión. En casos como este, los datos brutos de este en forma de ángulo y distancia serían medidas directas de\(\theta\) y\(r\) respectivamente. Los sistemas de coordenadas polares también servirán como base para el movimiento prolongado del cuerpo, donde los motores y actuadores pueden controlar directamente cosas como\(r\) y\(\theta\).

La forma en que se define el sistema de coordenadas, el\(r\) eje -siempre apuntará desde el punto de origen hasta el cuerpo. La distancia desde el origen hasta el punto se define como\(r\) sin componente de la posición que está en la\(\theta\) dirección.

\[ \text{Position:} \quad \, r_{p/o}(t) = r \hat{u}_r + 0 \ \hat{u}_{\theta} \]

Para encontrar la velocidad, necesitamos tomar la derivada de la función de posición a lo largo del tiempo. Dado que la distancia\(r\) puede cambiar con el tiempo así como la dirección que\(\hat{u}_r\) cambia con el tiempo para rastrear el cuerpo, debemos preocuparnos por la derivada del vector unitario así\(r\) como la derivada del vector unitario. Como hicimos con los sistemas normal-tangenciales, usaremos la regla del producto y luego sustituiremos en un valor la derivada del vector unitario.

\[ \text{Velocity:} \quad \, v(t) = \dot{r} \hat{u}_r + r \dot{\hat{u}}_r = \dot{r} \hat{u}_r + r \dot{\theta} \hat{u}_{\theta} \]

Para encontrar la aceleración, necesitamos tomar la derivada de la función de velocidad. Como todos estos términos, incluidos los vectores unitarios, cambian con el tiempo, necesitaremos usar ampliamente la regla del producto. El\(\hat{u}_r\) término se dividirá en dos términos, y el\(\hat{u}_{\theta}\) término se dividirá en tres términos.

\[ \text{Acceleration:} \quad \, a(t) = \ddot{r} \hat{u}_r + \dot{r} \dot{\hat{u}_r} + \dot{r} \dot{\theta} \hat{u}_{\theta} + r \ddot{\theta} \hat{u}_{\theta} + r \dot{\theta} \dot{\hat{u}}_{\theta} \]

Nuevamente tendremos que sustituir en valores las derivadas de los vectores unitarios similares a antes, pero vale la pena mencionar que la derivada del\(\hat{u}_{\theta}\) vector a medida que gira en sentido contrario a las agujas del reloj está en la\(\hat{u}_r\) dirección negativa.

Una partícula en el sistema de coordenadas polares gira en sentido antihorario en una pequeña cantidad d theta. El vector u-hat_r apunta desde la cabeza del vector de unidad de dirección r inicial hasta el vector de unidad de dirección r final, y el vector u-hat_theta apunta desde la cabeza del vector de unidad de dirección theta inicial hasta el vector de unidad de dirección theta final. — Figura\(\PageIndex{2}\): Las derivadas de los vectores\(\hat{u}_r\) y\(\hat{u}_{\theta}\) unitarios. Observe que la derivada del\(\hat{u}_{\theta}\) vector está en la\(\hat{u}_r\) dirección negativa.

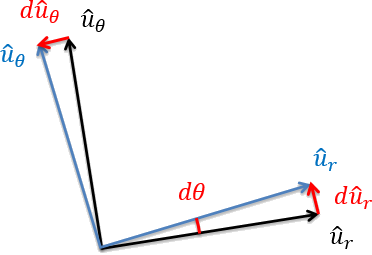
Después de sustituir en las derivadas de los vectores unitarios y simplificar la función, llegamos a nuestra ecuación final para la aceleración.

\ begin {align}\ text {Aceleración:}\ quad\, a (t) &=\ ddot {r}\ hat {u} _r +\ punto {r}\ punto {\ theta}\ hat {u} _ {\ theta} +\ punto {r}\ punto {\ theta}\ hat {u} _ {\ theta} + r\ ddot {\ theta}\ sombrero {u} _ {\ theta} - r\ punto {\ theta} ^2\ sombrero {u} _r\\ [5 pt] &=\ izquierda (\ ddot {r} - r\ punto {\ theta} ^2\ derecha)\ sombrero {u} _r +\ izquierda (2\ punto {r}\ punto {\ theta} + r\ ddot {\ theta}\ derecha)\ sombrero {u} _ {\ theta}\ end {align}

Aunque esta ecuación final tiene varios términos, sigue siendo solo dos componentes en forma de vector. Al igual que con el sistema de coordenadas normal-tangencial, tendremos que recordar que tendremos que dividir la ecuación de un solo vector en dos ecuaciones escalares separadas. En este caso tendremos la ecuación para los términos en la\(r\) dirección y la ecuación para los términos en la\(\theta\) dirección.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/F4i0Kz660aE.

Ejemplo\(\PageIndex{1}\)

Una estación de rastreo por radar proporciona los siguientes datos sin procesar a un usuario en un momento dado. Con base en estos datos, ¿cuál es la velocidad actual y la aceleración en las\(\theta\) direcciones\(r\) y? ¿Cuál es la velocidad actual y la aceleración en las\(y\) direcciones\(x\) y?

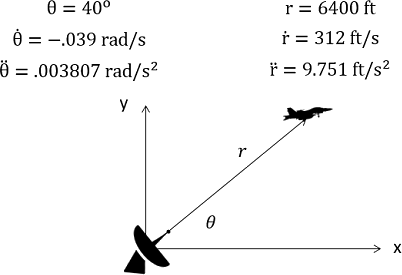
Avión ubicado en el primer cuadrante de un plano de coordenadas cartesianas, con una estación de rastreo por radar en el origen. Los datos de coordenadas polares de la posición actual del plano se dan como theta = 40 grados, theta-punto = -0.039 rad/s, theta doble punto = 0.003807 rad/s², r = 6400 ft, r-punto = 312 ft/s, y r doble punto = 9.751 ft/s². — Figura\(\PageIndex{3}\): Diagrama de problemas para Ejemplo\(\PageIndex{1}\). Los valores instantáneos de posición de coordenadas polares de un avión se dan como rastreados por una estación de radar, así como la primera y segunda derivadas de estas cantidades.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/HP4WiIa3Nc0.

Ejemplo\(\PageIndex{2}\)

Un foco está rastreando a un actor mientras se mueve por el escenario. Si el actor se mueve con una velocidad constante como se muestra a continuación, ¿qué valores necesitamos para la velocidad angular del foco\((\dot{\theta})\) y la aceleración angular del foco para\((\ddot{\theta})\) que el foco permanezca fijo en el actor?

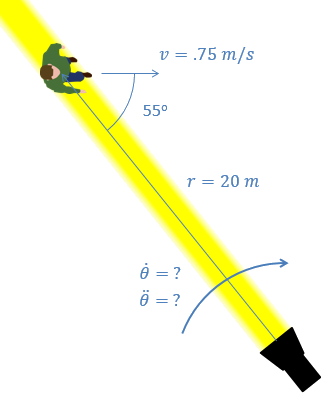
Una vista de arriba hacia abajo de un escenario con foco en la esquina inferior derecha, su haz brillando diagonalmente 20 metros a través del escenario sobre un actor en la esquina superior izquierda. El actor se mueve horizontalmente a 0.75 m/s hacia la derecha, 55 grados por encima de la línea diagonal del haz de foco. El foco gira en sentido horario para rastrear al actor. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un foco gira para seguir a un actor que se mueve a través del escenario a una velocidad conocida y comenzando desde una posición conocida en relación con el foco.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/jyD1seNQI14.