7.6: Sistemas de movimiento dependientes

Última actualización
Guardar como PDF

Page ID: 83926

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El análisis de movimiento dependiente se utiliza cuando dos o más partículas tienen movimientos que de alguna manera están conectados entre sí. La forma en que se conecta el movimiento de estas partículas se conoce como la restricción. Un ejemplo simple de un sistema restringido se muestra en la siguiente figura. Imagina que la camioneta de alguien se queda atascada en la arena, y un amigo usa una cuerda para ayudar a sacarla. Esta amiga ata un extremo de la cuerda al parachoques trasero de su auto, enrolla la cuerda alrededor de una barra en la parte delantera de la camioneta, luego ata el otro extremo a un árbol estacionario. En este caso los dos vehículos no tendrán la misma velocidad o aceleración, pero sus movimientos están relacionados porque están amarrados por la cuerda. En este caso, la cuerda está actuando como la restricción, permitiéndonos conocer la velocidad o aceleración de un vehículo en función de la velocidad o aceleración del otro vehículo.

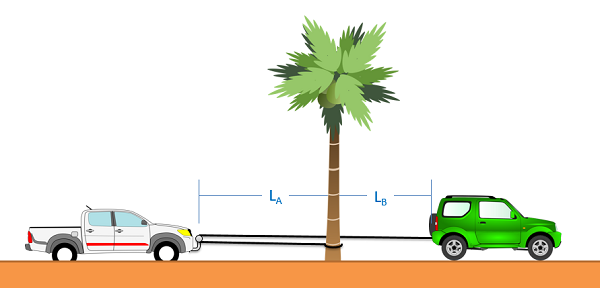
Una camioneta está atrapada en la arena al lado izquierdo de un árbol, y un automóvil está en el lado derecho del árbol. Una cuerda tiene un extremo atado al parachoques trasero del automóvil, se enrolla a través de un punto de fijación en la parte delantera del camión, y tiene su otro extremo atado al tronco del árbol. La cuerda está tensa y horizontal en todas partes. La distancia entre el árbol y el frente del camión está etiquetada como L_A, y la distancia entre el árbol y la parte trasera del automóvil está etiquetada como L_B. — Figura\(\PageIndex{1}\): Esto representa un sistema restringido. El movimiento del auto y la camioneta se relacionarán entre sí vía cuerda que los está conectando.

Lo primero que tendremos que hacer al analizar estos sistemas es llegar a lo que se conoce como la ecuación de restricción. Una ecuación de restricción será alguna relación geométrica que permanecerá cierta en el transcurso del movimiento. En el ejemplo anterior, imagina que la cuerda mide 50 pies de largo. Usando el árbol como punto estacionario, también podemos decir que la longitud de la cuerda es la distancia del auto verde al árbol, más dos veces la distancia de la camioneta al árbol (ya que debe salir a la camioneta y luego regresar). Si ponemos esto en una ecuación (la ecuación de restricción) tendríamos lo siguiente.

\[ \text{Constraint Equation: Positions} \quad \,\, \, L = 50 \, ft = 2 L_A + L_B \]

Una vez que tenemos una ecuación de restricción que funcione para las posiciones, podemos tomar la derivada de esta ecuación para encontrar otra ecuación de restricción que relacione las velocidades. En este caso, la longitud de la cuerda es constante, y por lo tanto la derivada de la longitud será cero. Si volvemos a tomar la derivada de la ecuación de restricción, terminamos con una tercera ecuación de restricción que relaciona las aceleraciones.

\ begin {align}\ text {Ecuación de restricción: Velocidades}\ quad &\,\,\ punto {L} = 0 = 2\ punto {L} _A +\ punto {L} _B\\ [5pt]\ text {Ecuación de restricción: aceleraciones}\ quad &\,\,\ ddot {L} = 0 = 2\ ddot {L} _A +\ ddot {L} _B\ end {align}

En estas ecuaciones, es importante recordar que los valores representan los cambios en la longitud, más que las medidas directas de las velocidades. Aunque ambos vehículos tendrían velocidades positivas en el ejemplo anterior (velocidades a la derecha), un\(\dot{L}\) valor será positivo y otro negativo. Esto se debe a que la camioneta se está acercando al árbol mientras el auto se aleja más. Una situación similar ocurrirá para las aceleraciones, donde ambos vehículos tendrían aceleraciones positivas aunque los\(\ddot{L}\) valores sean una mezcla de valores positivos y negativos.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/J1aPSrdDzdk.

Ejemplo\(\PageIndex{1}\)

Un camión queda atascado en la arena de una playa local. Para ayudar, una amiga toma una cuerda de 50 pies de largo, ata un extremo a su auto, enrolla la cuerda alrededor de una barra en la parte delantera de la camioneta y luego ata el otro extremo a un árbol estacionario como se muestra a continuación. Si el auto acelera a una velocidad de 0.2 pies/s², ¿cuál será la velocidad del camión para cuando llegue al árbol?

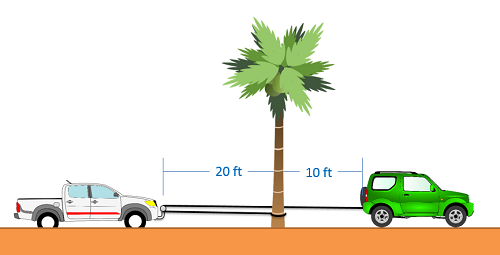
Una camioneta ubicada a 20 pies a la izquierda de un árbol está atrapada en la arena, y un automóvil está a 10 pies a la derecha del árbol. Una cuerda tiene un extremo atado al parachoques trasero del automóvil, se enrolla a través de un punto de fijación en la parte delantera del camión, y tiene su otro extremo atado al tronco del árbol. La cuerda está tensa y horizontal en todas partes. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una cuerda enrollada alrededor de la parte delantera de un camión, atada por un extremo al tronco de un árbol y en el otro al parachoques trasero de un automóvil, permite que el auto tire del camión de la arena en la que está atascado.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/IxO_Nrs7Kj0.

Ejemplo\(\PageIndex{2}\)

Un hombre ha conectado una polea, una cuerda y una plataforma como se muestra a continuación para levantar cargas en una azotea cercana. Si actualmente\(x\) es de 15 metros, actualmente\(y\) es de 5 metros, y el hombre se aleja del edificio a razón de 0.5 metros por segundo, ¿cuál es la velocidad actual de la plataforma?

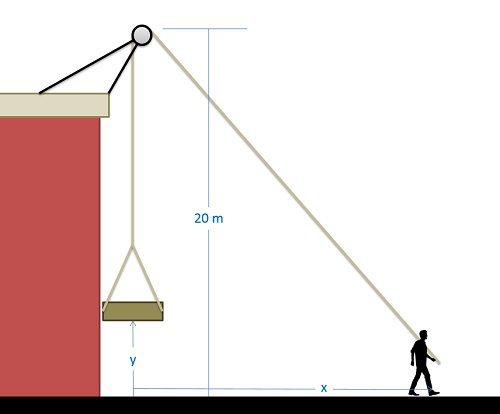
Una polea se encuentra en el techo del lado derecho de un edificio, a 20 metros sobre el suelo. Una cuerda corre a través de la polea, con un extremo atado a una carga y colgando del costado del edificio, y el otro extremo sostenido por un hombre en el suelo a la derecha del edificio. A medida que el hombre camina más hacia la derecha, su distancia del edificio (x) y la altura de la carga sobre el suelo (y) aumentan ambas. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un hombre se aleja de un edificio de 20 metros de altura, sosteniendo un extremo de una cuerda que pasa sobre una polea en la azotea y levanta una carga en su otro extremo.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/z3D_2jHLCik.