7.7: Sistemas de movimiento relativo

Última actualización
Guardar como PDF

Page ID: 83918

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El análisis de movimiento relativo es el análisis de cuerpos donde más de un cuerpo está en movimiento y de alguna manera estamos examinando el movimiento de una partícula en movimiento en relación con otra partícula en movimiento. Un ejemplo serían los autos en una autopista. Si estás en uno de los muchos autos bajando por un lado de la autopista, tú y los otros autos tendrán velocidades en una sola dirección. Sin embargo, desde tu perspectiva dentro del auto, los autos rápidos frente a ti parecerán estar alejándose de ti y los autos lentos frente a ti parecerán estar moviéndose hacia ti. Al conocer tu velocidad, y al observar qué tan rápido se mueven los autos lejos de ti o hacia ti, podrías determinar o al menos estimar qué tan rápido van estos autos. El proceso de usar su velocidad junto con las velocidades relativas de los otros autos para encontrar la velocidad de los otros autos es el análisis de movimiento relativo.

Movimiento relativo en una dimensión:

En una sola dimensión, normalmente tendremos al menos dos partículas móviles así como algún punto de referencia fijo. Usualmente llamamos al punto de referencia fijo\(O\), y luego etiquetamos los otros puntos\(A\),\(B\), y así sucesivamente. En el diagrama, a continuación podemos ver un ejemplo de esto, con un punto de referencia fijo en\(O\), un carro de policía en\(A\), y un automóvil a exceso de velocidad en\(B\).

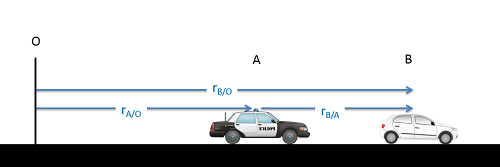
Una carretera recta donde un punto de referencia del lado izquierdo está etiquetado como O. Un automóvil que conduce a la derecha se encuentra en el extremo derecho de la imagen, en el punto B, y un carro de policía que se mueve en la misma dirección que el automóvil se ubica ligeramente más cerca de O, en el punto A. La distancia del carro de O se da como R_b/o, la distancia del auto del carro de policía se da como R_b/a, y la distancia del carro de policía de O se da como R_a/o. — Figura\(\PageIndex{1}\): En una sola dimensión tenemos un punto de referencia fijo\(O\), así como al menos dos cuerpos móviles (etiquetados como\(A\) y\(B\) en este caso). Los\(r\) vectores representan las distancias entre cuerpos, con el subíndice indicando el punto que estamos observando y el punto desde el que estamos observando. Los subíndices deben tener siempre el siguiente formato: punto que se observa/punto desde el que estamos observando.

Como podemos ver en el diagrama anterior, la suma de la distancia de\(O\) a\(A\)\((r_{A/O})\) y la distancia de\(A\) a\(B\)\((r_{B/A})\) será igual a la distancia de\(O\) a\(B\)\((r_{B/O})\). Esto nos da nuestra ecuación de posición a continuación.

\[ \text{Position:} \quad \, r_{B/O} = r_{A/O} + r_{B/A} \]

Una cosa que debemos notar sobre los subíndices es que si nos mantenemos a nuestra convención de nomenclatura estándar (punto que se observa/punto desde el que estamos observando) entonces deberíamos poder ver qué puntos cancelan y cuáles quedan. En este caso, las\(A\)'s en la parte superior e inferior a la derecha cancelan, dejando solo una\(B\) en la parte superior y una\(O\) en la parte inferior. Esto coincide con el subíndice de la izquierda de la ecuación.

Además, podemos tomar la derivada de esta ecuación para relacionar velocidades, o una derivada doble para relacionar aceleraciones. Esto quiere decir que si conocemos dos de los términos en las ecuaciones siguientes, podemos resolver para el tercero.

\ begin {align}\ text {Velocidad:}\ quad &\, v_ {B/O} = v_ {A/O} + v_ {B/A}\\ [5pt]\ text {Aceleración:}\ quad &\, a_ {B/O} = a_ {A/O} + a_ {B/A}\ end {align}

Movimiento relativo en dos dimensiones:

Al igual que con una dimensión, podemos comenzar examinando un conjunto de posiciones relativas. En este caso usaremos el ejemplo de dos planos que se mueven por el cielo. Es posible que deseemos deducir la posición del plano B en un mapa, en base a nuestras observaciones del plano A. Al usar la información que tenemos sobre nuestra posición relativa a alguna ubicación establecida, junto con la posición relativa leída desde la instrumentación a bordo, deberíamos poder determinar la posición absoluta (incluyendo una \(x\)y\(y\) coordenada) para el plano B.

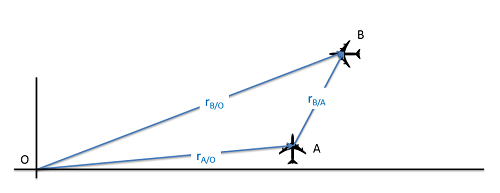
El primer cuadrante de un plano de coordenadas cartesianas, en el que se marca un avión A en la ubicación A y otro avión B está marcado en la ubicación B. El vector R_a/o apunta desde el origen O a la ubicación del plano A, el vector R_b/A apunta desde la ubicación del plano A a la ubicación del plano B, y el vector R_b/o apunta desde el origen hasta la ubicación del avión B. — Figura\(\PageIndex{2}\): En dos dimensiones tenemos un punto de referencia fijo\(O\), así como al menos dos cuerpos móviles (etiquetados como\(A\) y\(B\) en este caso). Los\(\vec{r}\) vectores representan los vectores de distancia entre cuerpos, con el subíndice indicando el punto inicial y final. Los subíndices siempre deben ser formateados punto final/punto de partida.

En dos dimensiones, usaremos las mismas ecuaciones que antes, excepto que esta vez usaremos vectores en lugar de valores escalares en nuestras ecuaciones.

\ begin {align}\ text {Posición:}\ quad &\,\ vec {r} _ {B/O} =\ vec {r} _ {A/O} +\ vec {r} _ {B/A}\\ [5pt]\ text {Velocidad:}\ quad &\,\ vec {v} _ _ {B/O} =\ vec {v} _ {A/O} +\ vec c {v} _ {B/A}\\ [5pt]\ text {Aceleración:}\ quad &\,\ vec {a} _ {B/O} =\ vec {a} _ {A/O} +\ vec {a} _ {B/A}\ end {align}

Para resolver estas ecuaciones, casi siempre dividiremos las ecuaciones vectoriales en un conjunto de ecuaciones de componentes. Esto nos permitirá resolver estas ecuaciones con álgebra simple. Debido a que tenemos más de una partícula, generalmente usamos sistemas de coordenadas rectangulares para esto con un conjunto universal de\(x\) y\(y\) coordenadas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/A5aJ2VYvwkw.

Ejemplo\(\PageIndex{1}\)

Un oficial de policía advierte que un automóvil pasa por exceso de velocidad. Si el carro de policía viaja 30 m/s y la pistola radar mide la velocidad relativa para ser de 15 m/s, ¿qué tan rápido va realmente el auto a exceso de velocidad? Si el auto de policía inmediatamente comienza a acelerar a un ritmo constante y alcanza al auto a toda velocidad después de 15 segundos, ¿cuál es la tasa de aceleración del auto policial?

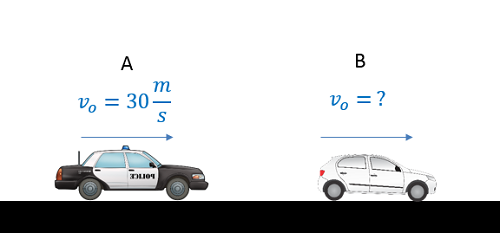
Un carro de policía en la posición A, en el lado izquierdo de la imagen, se desplaza hacia la derecha a una velocidad inicial de 30 m/s. Un carro en la posición B, en el lado derecho de la imagen, se desplaza hacia la derecha a cierta velocidad inicial. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un carro de policía y un auto a toda velocidad que persigue después de viajar en la misma dirección por una carretera recta.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/YndovN5yWfc.

Ejemplo\(\PageIndex{2}\)

Un avión tiene una velocidad aérea de 250 kilómetros por hora (la velocidad del aire es la velocidad del avión relativa al aire) y está volando a través de un viento cruzado este con una velocidad de 20 kilómetros por hora. Si el avión quiere mantener un rumbo directo hacia el norte, ¿cuál es el ángulo que el avión debe apuntar al viento\((\theta)\)?

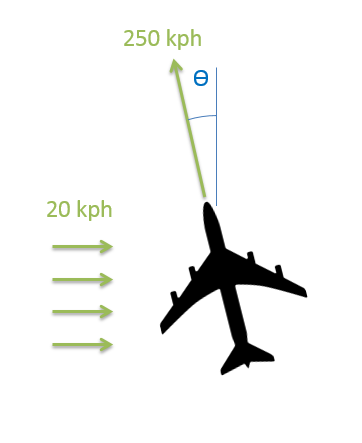
Vista de arriba hacia abajo de un avión volando a 250 km/h en un ángulo de theta al oeste del norte directo. Esto se representa en la imagen como el plano apuntando ligeramente a la izquierda de la vertical. El avión también experimenta vientos de 20 kph soplando directamente hacia el este (hacia la derecha de la imagen). — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un avión que tiene como objetivo volar directamente hacia el norte experimenta vientos cruzados del este.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/ga1qcV38zYA.

Ejemplo\(\PageIndex{3}\)

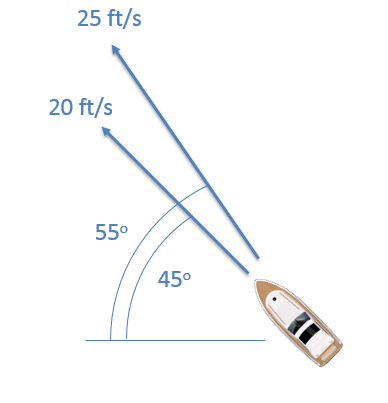
Estás en una embarcación que viaja por el agua en una zona de corrientes rápidas. Un instrumento mide tu velocidad con respecto al agua para ser de 20 pies/s con tu embarcación apuntando en un ángulo de 45 grados. El GPS, sin embargo, mide tu velocidad y dirección absolutas para ser de 25 pies/s en un ángulo de 55 grados. Con base en esta información, ¿cuál es la velocidad y dirección de la corriente de agua en esta zona?

Vista de arriba hacia abajo de una embarcación apuntando hacia la esquina superior izquierda de la imagen. Un vector de velocidad para la embarcación tiene una magnitud de 20 pies/s y está 45 grados por encima del eje x negativo. Otro vector de velocidad para la embarcación tiene una magnitud de 25 f/s y marcas es 55 grados por encima del eje x negativo. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Los instrumentos en una embarcación devuelven diferentes lecturas para su velocidad absoluta vs. su velocidad relativa al agua circundante.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/j8vnM_hrnQg.