8.3: Ecuaciones de Movimiento en Coordenadas Normal-Tangenciales

Última actualización
Guardar como PDF

Page ID: 83787

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Continuando con nuestra discusión sobre la cinética en dos dimensiones, podemos examinar la Segunda Ley de Newton aplicada al sistema de coordenadas normal-tangencial. En su forma básica, la Segunda Ley de Newton establece que la suma de las fuerzas sobre un cuerpo será igual a la masa de ese cuerpo multiplicada por la velocidad de aceleración. Para los cuerpos en movimiento, podemos escribir esta relación como la ecuación del movimiento.

\[ \sum \vec{F} = m * \vec{a} \nonumber \]

Al igual que hicimos con coordenadas rectangulares, vamos a romper esta ecuación de vector único en dos ecuaciones escalares separadas. Esto implica identificar las direcciones normal y tangencial y luego usar senos y cosenos para romper las fuerzas y aceleraciones dadas hacia abajo en componentes en esas direcciones.

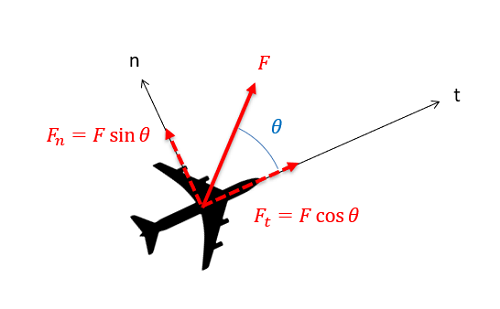
Un plano mira hacia la esquina superior derecha de la imagen, moviéndose a lo largo del eje tangencial. El eje normal se ubica a 90 grados en sentido contrario a las agujas del reloj del eje tangencial. El plano experimenta una fuerza F, que forma un ángulo de theta por encima del eje tangencial. Esa fuerza total se divide en el componente n, que es igual a la magnitud de F por el coseno theta, y el componente t, que es igual a la magnitud de F por el seno de theta. — Figura\(\PageIndex{1}\): Cuando se trabaja en el sistema de coordenadas normal-tangencial, cualquier fuerza o aceleración dada se puede descomponer usando senos y cosenos siempre y cuando se conozca el ángulo de la fuerza o aceleración en relación con las direcciones normal y tangencial.

\ begin {align}\ suma f_n &= m * a_n\\ [5pt]\ suma f_t &= m * a_t\ end {align}

Al igual que con las coordenadas rectangulares, estas ecuaciones de movimiento se utilizan a menudo en conjunto con las ecuaciones cinemáticas, que relacionan posiciones, velocidades y aceleraciones como se discutió en el capítulo anterior. En particular, a menudo sustituiremos los valores conocidos a continuación por los componentes normales y tangenciales para la aceleración.

\[ a_n = v * \dot{\theta} = \frac{v^2}{\rho} \]

\[ a_t = \dot{v} \]

Las coordenadas normal-tangenciales se pueden utilizar en cualquier problema cinético; sin embargo, funcionan mejor con problemas donde las fuerzas mantienen una dirección consistente en relación con algún cuerpo en movimiento. Los vehículos en movimiento son un buen ejemplo de esto: la dirección de las fuerzas aplicadas depende en gran medida de la dirección actual del vehículo, y estas fuerzas girarán con el vehículo a medida que gira.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/PK2swJu37sg.

Ejemplo\(\PageIndex{1}\)

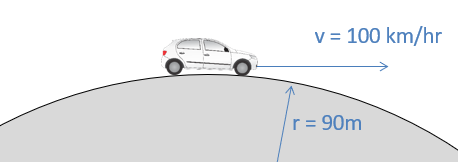
Un automóvil de 1000 kg recorre una colina a una velocidad constante de 100 kilómetros por hora. La cima del cerro se puede aproximar como un círculo con un radio de 90 metros.

¿Cuál es la fuerza normal que ejerce la carretera sobre el automóvil mientras abraza el cerro?
¿Qué tan rápido tendría que estar el auto para llegar al aire?

Una vista lateral de una colina se representa como una porción de un círculo con un radio de 90 metros. Un automóvil en la cima de la colina conduce hacia la derecha a una velocidad de 100 km/h. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un automóvil se encuentra en lo alto de una colina, moviéndose hacia la derecha a una velocidad constante de 100 km/hr.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/KOLdXpQ5M1Q.

Ejemplo\(\PageIndex{2}\)

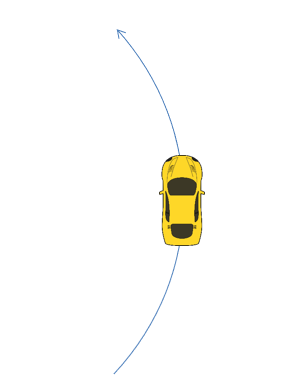
Un automóvil de 2500 libras viaja 40 pies por segundo. El coeficiente de fricción entre las llantas del automóvil y la carretera es de 0.9.

Si el automóvil mantiene una velocidad constante, ¿cuál es el radio mínimo de curvatura antes de deslizarse?
Suponiendo que el automóvil está acelerando a una velocidad de 10 pies/s², ¿cuál es el radio mínimo de curvatura antes de deslizarse?

Vista de arriba hacia abajo de un automóvil viajando a lo largo de un camino curvo que parece ser una sección de un círculo. La posición actual del automóvil está en el punto más a la derecha del círculo, mirando hacia la parte superior de la imagen por lo que se desplaza alrededor del círculo en sentido contrario a las agujas del reloj. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un automóvil recorre una trayectoria circular en sentido contrario a las agujas del reloj.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/Gw0_H0wdqm8.

Ejemplo\(\PageIndex{3}\)

Las cajas de 15 kg se transportan alrededor de una curva a través de una cinta transportadora, como se muestra a continuación. Suponiendo que la curva tiene un radio de 3 metros y las cajas se desplazan a una velocidad constante de 1 metro por segundo, ¿cuál es el coeficiente mínimo de fricción necesario para asegurar que las cajas no se deslicen mientras viajan alrededor de la curva?

Una sección nivelada de cinta transportadora que es de forma semicircular. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\); una sección nivelada de cinta transportadora en forma semicircular.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/4z73Pc3s_TE.