8.4: Ecuaciones de Movimiento en Coordenadas Polares

Última actualización
Guardar como PDF

Page ID: 83788

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para terminar nuestra discusión sobre las ecuaciones del movimiento en dos dimensiones, examinaremos la Segunda ley de Newton tal como se aplica al sistema de coordenadas polares. En su forma básica, la Segunda Ley de Newton establece que la suma de las fuerzas sobre un cuerpo será igual a la masa de ese cuerpo multiplicada por la velocidad de aceleración. Para los cuerpos en movimiento, podemos escribir esta relación como la ecuación del movimiento.

\[ \sum \vec{F} = m * \vec{a} \nonumber \]

Al igual que hicimos con las coordenadas rectangulares y normal-tangenciales, dividiremos esta ecuación de vector único en dos ecuaciones escalares separadas. Esto implica identificar las\(\theta\) direcciones\(r\) y y luego usar senos y cosenos para romper las fuerzas y aceleraciones dadas en componentes en esas direcciones.

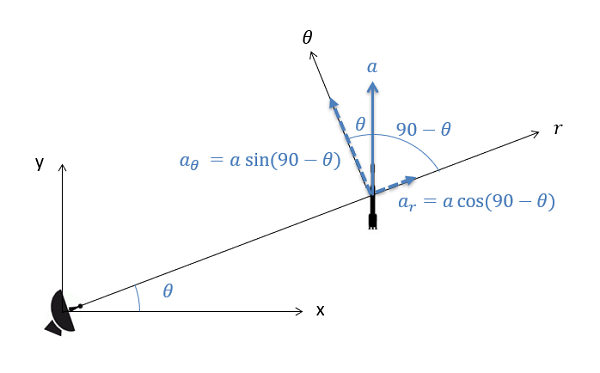
El primer cuadrante de un plano de coordenadas cartesianas se representa con una estación de radar en el origen, y un misil siendo rastreado a una distancia de r del origen y un ángulo de grados Theta por encima del eje x. El misil actualmente está acelerando directamente hacia arriba en la dirección y. Su aceleración neta se divide en aceleración en la dirección r, continuando en la dirección del vector r, y aceleración en la dirección theta, 90 grados en sentido antihorario desde la dirección r. El eje theta está en un ángulo de grados Theta a la izquierda del vector de aceleración neta. Aceleración_theta = magnitud de los tiempos de aceleración netos sin (90° - Theta), y aceleración_r = magnitud de los tiempos de aceleración netos cos (90° - Theta). — Figura\(\PageIndex{1}\): Cuando se trabaja en el sistema de coordenadas polares, cualquier fuerza o aceleración dada se puede descomponer usando senos y cosenos siempre y cuando se conozca el ángulo de la fuerza o aceleración en relación con las\(\theta\) direcciones\(r\) y.

\ begin {align}\ suma f_r &= m * a_r\\ [5pt]\ suma F_ {\ theta} &= m * a_ {\ theta}\ end {align}

Al igual que con nuestros otros sistemas de coordenadas, las ecuaciones de movimiento se utilizan a menudo en conjunto con las ecuaciones cinemáticas, que relacionan posiciones, velocidades y aceleraciones como se discutió en el capítulo anterior. En particular, a menudo sustituiremos los valores conocidos a continuación por los\(\theta\) componentes\(r\) y para la aceleración.

\[ a_r = \ddot{r} - r \theta^2 \]

\[ a_{\theta} = 2 \dot{r} \dot{\theta} + r \ddot{\theta} \]

Las coordenadas polares se pueden usar en cualquier problema cinético; sin embargo, funcionan mejor con problemas donde hay un cuerpo estacionario que rastrea algún cuerpo en movimiento (como una antena parabólica de radar) o hay una partícula girando alrededor de algún punto fijo. Estas ecuaciones también volverán a entrar en juego cuando comencemos a examinar la cinemática del cuerpo rígido.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/XiuQSSVdRKk.

Ejemplo\(\PageIndex{1}\)

Un dispositivo consta de dos masas, cada una de 0.5 kg de masa, atadas a un eje central. Las ataduras son cada una de 0.75 metros de largo y cada correa actualmente forma un ángulo de 25 grados con el eje central. Supongamos que el eje central está girando a una velocidad constante. ¿Cuál es la velocidad a la que gira el eje? Si queremos que gire exactamente a 100 rpm, ¿cuál debería ser el ángulo de las ataduras?

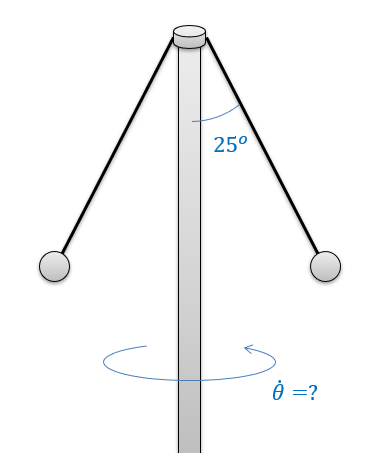
Un eje central vertical tiene dos cuerdas idénticas colgando del extremo superior, una en el lado izquierdo del eje y la otra en el lado derecho. Cada correa soporta una masa esférica idéntica y forma un ángulo de 25° con el eje. El eje gira en sentido contrario a las agujas del reloj, a la velocidad punto-theta. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un eje giratorio soporta dos ataduras idénticas en su extremo superior, cada una de las cuales sostiene una masa y se extiende simétricamente desde el eje.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/fGsoMdR1H9I.

Ejemplo\(\PageIndex{2}\)

Un diseño de catapulta consiste en un peso de acero sobre una varilla sin fricción. La varilla gira a una velocidad constante de 4 radianes por segundo y cuando\(\theta\) está a 45 grados de la horizontal, el peso de 30 lb se libera de su posición a 2 pies del centro de rotación del eje. ¿Cuál es la fuerza que ejerce el eje sobre el peso en el instante anterior y en el instante posterior a su liberación? ¿Cuál es la aceleración del peso a lo largo del eje en el instante en que se libera?

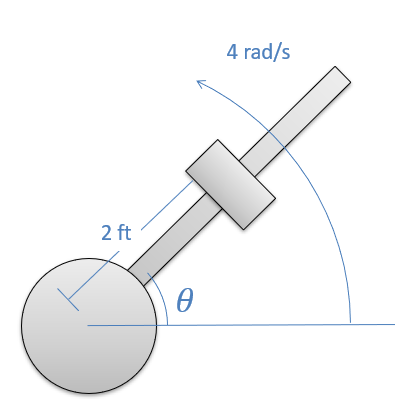
Vista de arriba hacia abajo de un eje vertical central que soporta una varilla horizontal. Se coloca un peso sobre la varilla, a una distancia de 2 pies del centro de rotación del eje vertical. La varilla gira en sentido antihorario a una velocidad de 4 rad/s, haciendo un ángulo de theta con la línea horizontal que se extiende a la derecha del eje central. El valor theta actual está 45 grados por encima de esa línea horizontal. — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un eje vertical central que gira soporta una varilla horizontal que lleva un peso liberable.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/bKsi80wzLUY.