10.5: Dispositivos de flujo constante

Última actualización
Guardar como PDF

Page ID: 83964

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un dispositivo de flujo constante es cualquier dispositivo que tendrá un flujo continuo de material a través de él. Algunos ejemplos de dispositivos de flujo constante incluyen tuberías, boquillas, difusores y bombas. Generalmente, el material que fluye a través del dispositivo es un gas o líquido, y si el dispositivo cambia de alguna manera la velocidad del fluido entonces ese fluido ejercerá una fuerza sobre el dispositivo de flujo constante a cambio.

Un equipo de bomberos operando una manguera contra incendios en un ejercicio de entrenamiento. — Figura\(\PageIndex{1}\): La boquilla de la manguera contra incendios es un ejemplo de un dispositivo de flujo constante. Debido a que la boquilla cambia la velocidad del agua a medida que sale de la manguera, tomará una fuerza para mantener la boquilla en su lugar.

Para determinar las fuerzas en juego en un dispositivo de flujo constante, comenzaremos con nuestra ecuación impulso-impulso.

\[ \vec{J} = m \vec{v}_f - m \vec{v}_i \]

Debido a que este es un proceso continuo, realmente no tiene sentido tener velocidades iniciales y finales. En cambio, tendremos velocidades de entrada y salida. Además, la masa deberá cambiarse al caudal másico (la masa que entra o sale del dispositivo por unidad de tiempo) para hacer frente a la naturaleza de flujo continuo del sistema.

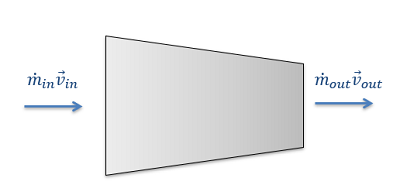
Un trapecio simétrico con la base más larga en el lado izquierdo. Este lado más ancho representa el caudal másico de entrada y la velocidad de entrada, que se cambia por el funcionamiento del dispositivo a un caudal másico de salida diferente y velocidad de salida (que sale del dispositivo a través de la base más estrecha del lado derecho del trapecio). — Figura\(\PageIndex{2}\): El caudal másico es una medida más apropiada para los dispositivos de flujo constante que la masa estándar.

Dividir nuestra ecuación inicial impulso-impulso por tiempo en ambos lados nos dará el caudal másico deseado a la derecha, mientras que el tiempo a la izquierda cancelará la componente de tiempo del impulso.

\[ \frac{\vec{F} * t}{t} = \frac{m_{out}}{t} \vec{v}_{out} - \frac{m_{in}}{t} \vec{v}_{in} \]

Simplificando esta ecuación, llegaremos a nuestra ecuación final, que relaciona la fuerza que nuestro dispositivo de flujo constante ejerce sobre el fluido con los caudales másticos y velocidades en la entrada y salida. La fuerza que el fluido ejerce sobre el dispositivo sería simplemente igual y opuesta a la fuerza inferior.

\[ \vec{F} = \dot{m}_{out} \vec{v}_{out} - \dot{m}_{in} \vec{v}_{in} \]

Una nota final es que estas ecuaciones son ecuaciones vectoriales. Si el dispositivo está cambiando la dirección del flujo de un fluido, deberá romper la fuerza y las velocidades en\(x\) y\(y\) componentes y dividir la ecuación anterior en\(x\) y\(y\) componentes.

Encontrar el caudal másico:

Si el caudal másico dentro o fuera de su dispositivo no se da directamente, es posible que deba encontrar esos valores. Primero podemos usar una identidad simple: sabemos que el caudal másico será igual a la densidad del fluido\((\rho)\) multiplicado por el caudal volumétrico. Además, el caudal volumétrico puede estar relacionado con la geometría del dispositivo, ya que será igual a la velocidad promedio del fluido en la entrada o salida multiplicado por el área de sección transversal en la entrada o salida. Armando todo esto, llegamos a la siguiente fórmula.

\[ \dot{m} = \rho \dot{V} = \rho \vec{v} A \]

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/R8A35UeoNyE.

Ejemplo\(\PageIndex{1}\)

Un bombero soporta una manguera como se muestra a continuación. La manguera tiene un caudal volumétrico de 60 gal/min y la boquilla reduce en diámetro de 4 cm a 2 cm. ¿Qué fuerza tendrá que ejercer el bombero, en Newtons, para mantener la manguera en su lugar?

Dos bomberos sujetan el cuerpo de una manguera contra incendios mientras rocía agua, mientras que un tercer bombero controla la dirección de la boquilla de la manguera. — Figura\(\PageIndex{3}\): Un bombero que sostiene la boquilla de una manguera. Foto de Macomb Paynes, CC BY-NC-SA 2.0.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/rl4A1N_BNGA.

Ejemplo\(\PageIndex{2}\)

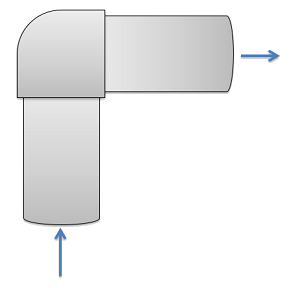
Una articulación acodada de 90 grados redirige el flujo a lo largo de una tubería de 3 cm de diámetro. Si el agua (densidad=1000 kg/m ³) está viajando por la tubería con una velocidad promedio de 5 m/s, ¿cuál es la magnitud y dirección de la fuerza que ejerce el agua sobre la articulación del codo?

Una junta acodada de 90° conecta una longitud de tubería que se extiende desde la parte inferior izquierda de la imagen hasta la parte superior izquierda hasta una segunda longitud de tubería que se extiende desde la parte superior izquierda de la imagen hasta la parte superior derecha. El agua fluye hacia este conjunto en la abertura en la parte inferior izquierda, y sale por la abertura en la parte superior derecha. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un conjunto en forma de L invertida de dos segmentos de tubería conectados por una articulación acodada tiene agua que ingresa a través de la abertura inferior izquierda y sale a través de la abertura superior derecha.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/znKq2quYMWk.