11.3: Análisis de Movimiento Absoluto

Última actualización
Guardar como PDF

Page ID: 83901

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El análisis de movimiento absoluto es un método utilizado para analizar cuerpos sometidos a movimiento plano general. El movimiento plano general es el movimiento donde los cuerpos pueden trasladarse y rotar al mismo tiempo. Además del análisis de movimiento absoluto, la alternativa es el análisis de movimiento relativo. Cualquiera de los dos métodos se puede utilizar para cualquier problema general de movimiento plano, pero un método puede ser significativamente más fácil de aplicar para una situación dada.

El análisis de movimiento absoluto requerirá cálculo, y generalmente es más rápido para problemas simples y problemas donde solo se requieren las velocidades (y no aceleraciones). El análisis de movimiento relativo no requerirá cálculo, pero sí requiere el uso de múltiples sistemas de coordenadas; generalmente es más fácil de usar para problemas más complejos y problemas donde se están analizando velocidades y aceleraciones.

Utilizando Análisis de Movimiento Absoluto:

Para iniciar nuestra discusión sobre el análisis de movimiento absoluto, vamos a imaginar un brazo robótico simple como el de abajo. En este brazo, tenemos dos secciones de brazo de longitud fija con motores que provocan rotaciones en la articulación A y la junta B.

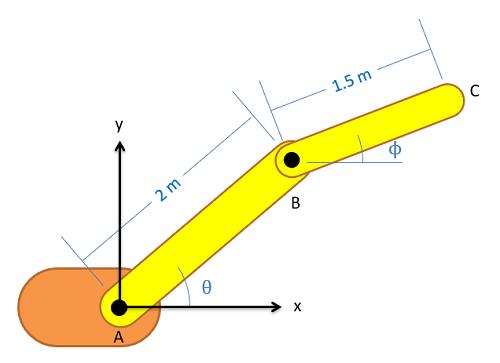
AB, un segmento de brazo robótico de 2 metros de largo con su base siendo el punto A, se estira hacia arriba y hacia la derecha para formar un ángulo de theta con el eje x positivo de un plano cartesiano de orientación estándar con el origen centrado en el punto A. BC, un segmento de brazo robótico de 1.5 metros de largo, se conecta al extremo libre del segmento AB y se estira hacia arriba y hacia la derecha, haciendo un ángulo de phi con la horizontal. — Figura\(\PageIndex{1}\): Este brazo robótico tiene una base fija en A, y dos secciones de brazo de longitud fija (AB y BC) que se controlan mediante motores en las articulaciones A y B. El efector final del brazo robótico está en C.

El primer paso en el análisis de movimiento absoluto es llegar a un conjunto de ecuaciones que describan la posición de algún punto de interés. En este caso estaremos mirando la posición del efector final del brazo en el punto C, y escribiremos una ecuación para la\(x\) posición y la\(y\) posición de este punto con respecto al punto de origen fijo en A. En estas ecuaciones, cualquier cosa que sea una constante (como la longitud del piezas de brazo) se pueden poner como un número, pero cualquier cosa que cambie, como ángulos\(\theta\) y\(\phi\), tendrá que permanecer como variables en estas ecuaciones aunque se conozcan en este momento. Usando los valores en el diagrama, terminaríamos con las siguientes dos ecuaciones de posición.

\ begin {align} x\ text {-posición:}\ quad &\, x_C = 2\ cos (\ theta) + 1.5\ cos (\ phi)\\ [5pt] y\ text {-posición:}\ quad &\, y_C = 2\ sin (\ theta) + 1.5\ sin (\ phi)\ end {align}

Para encontrar la velocidad del punto C en las\(y\) direcciones\(x\) y, simplemente necesitamos tomar las derivadas de las ecuaciones de posición. Las ecuaciones de velocidad para nuestro brazo robótico están abajo.

\ begin {align} x\ text {-velocidad:}\ quad &\, v_ {x\ C} = -2\ sin (\ theta)\ punto {\ theta} - 1.5\ sin (\ phi)\ punto {\ phi}\\ [5pt] y\ text {-velocidad:}\ quad &\, v_ {y\ C} = 2\ cos (\ theta)\ punto {\ theta} + 1.5\ cos (\ phi)\ punto {\ phi}\ end {align}

Para encontrar la aceleración del punto C en las\(y\) direcciones\(x\) y, simplemente necesitamos tomar las derivadas de las ecuaciones de velocidad. Las ecuaciones de aceleración para nuestro brazo robótico en las\(y\) direcciones\(x\) y se muestran a continuación.

\ begin {align} x\ text {aceleración:}\ quad &\, a_ {x\ C} = -2\ cos (\ theta)\ punto {\ theta} ^2 - 2\ sin (\ theta)\ ddot {\ theta} - 1.5\ cos (\ phi)\ punto {\ phi} ^2 - 1.5\ sin (\ phi)\ ddot {phi}\\ [5pt] y\ texto {aceleración:}\ quad &\, a_ {y\ C} = -2\ sin (\ theta)\ punto {\ theta} ^2 + 2\ cos (\ theta)\\ ddot {\ theta} - 1.5\ sin (\ phi)\\ punto {\ phi} ^2 + 1.5\ cos (\ phi)\ ddot {\ phi}\ end {align}

Una vez que tenemos las ecuaciones de velocidad y aceleración, podemos comenzar a resolver cualquier incógnitas. Si hemos conocido velocidades angulares y aceleraciones (\(\dot{\theta}\),\(\ddot{\theta}\)\(\dot{\phi}\), y\(\ddot{\phi}\)) podemos conectarlas para encontrar los vectores de velocidad y aceleración para el efector final. En otros casos, podemos conocer el movimiento deseado del efector final (\(v_{xC}\),\(v_{yC}\)\(a_{xC}\), y\(a_{yC}\)) y tendremos que enchufar esos valores en las ecuaciones para resolver incógnitas como\(\dot{\theta}\) y así sucesivamente.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/y1Pq2VP3qas.

Ejemplo\(\PageIndex{1}\)

El brazo robótico que se muestra a continuación tiene una base naranja fija en A y miembros de longitud fija AB y BC. Los motores en A y B permiten el movimiento de rotación en las juntas. Con base en las velocidades angulares y aceleraciones mostradas en cada articulación, determinar la velocidad y la aceleración del efector final en C.

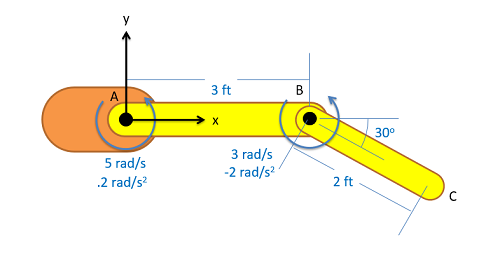
Un miembro horizontal AB de 3 pies de largo está fijado a una base inmóvil en su extremo izquierdo, punto A. Un motor en el punto A proporciona una rotación en sentido contrario a las agujas del reloj de 5 rad/s y 0.2 rad/s². Un miembro de 2 pies de largo, BC, se estira hacia abajo y hacia la derecha desde el punto final derecho del miembro AB, a 30° por debajo de la horizontal. Un motor en el punto B proporciona una rotación en sentido contrario a las agujas del reloj de 3 rad/s y -2 rad/s². — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un brazo robótico con dos segmentos tiene motores en sus articulaciones, que giran a velocidades y aceleraciones conocidas.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/ZBj17t8mhZc.

Ejemplo\(\PageIndex{2}\)

El brazo robótico del problema anterior se encuentra en la configuración que se muestra a continuación. Supongamos que actualmente\(\theta\) es de 30 grados y que el punto C actualmente se encuentra a lo largo del\(x\) eje. Si queremos que el efector final en C viaje 1 pies/s en la\(x\) dirección negativa, ¿cuáles deberían ser las velocidades angulares en las juntas A y B?

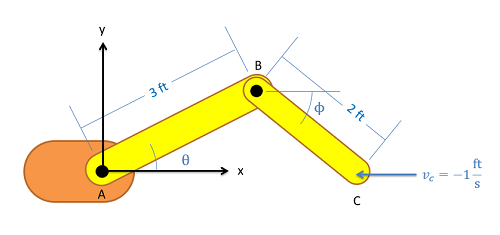
El miembro AB de 3 pies de largo tiene su punto final izquierdo, A, unido a una base fija y se estira hacia arriba y hacia la derecha, formando un ángulo de theta por encima de la horizontal. Un plano cartesiano de orientación estándar se centra en el punto A. El miembro BC de 2 pies de largo se extiende hacia abajo y hacia la derecha desde el extremo libre de AB, en un ángulo de phi debajo de la horizontal. El efector final en el punto C, el extremo libre del miembro BC, se mueve horizontalmente hacia la izquierda a 1 pies/s (en la dirección x negativa). — Figura\(\PageIndex{3}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un brazo robótico de dos segmentos tiene un efector en su extremo libre que se mueve a una velocidad conocida, como resultado de la rotación de los motores en las dos juntas.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/O5mtTTpK1RQ.

Ejemplo\(\PageIndex{3}\)

Una escalera está apoyada contra una pared como se muestra a continuación. Si la base de la escalera se desliza a una velocidad de 2 m/s, ¿cuál es la velocidad de la parte superior de la escalera?

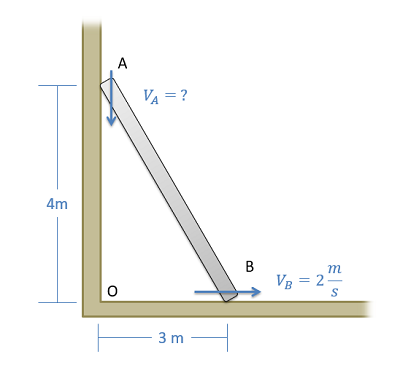
Vista lateral de una pared y una escalera apoyada contra el lado derecho de esa pared. El extremo de la escalera en la pared, A, está a 4 pies sobre el piso. El extremo de la escalera en el piso, B, está a 3 pies a la derecha de la pared y se desliza hacia la derecha a 2 m/s. El punto de intersección entre la pared y el piso está etiquetado como punto O. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una escalera apoyada contra una pared está cayendo, ya que su pie se desliza alejándose de la pared.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/fOfEaFUiDZI.

Ejemplo\(\PageIndex{4}\)

El mecanismo biela-balancín como se muestra a continuación consiste en una manivela con un radio de 0.5 metros que gira alrededor de su centro fijo en C, a una velocidad constante de 2 rad/s en sentido horario. El balancín AB se fija en su base en A y se conecta al punto B a lo largo del borde de la manivela. El pasador en el punto B puede deslizarse a lo largo de una ranura sin fricción en AB. En el estado actual, ¿cuál es la velocidad angular del balancín AB?

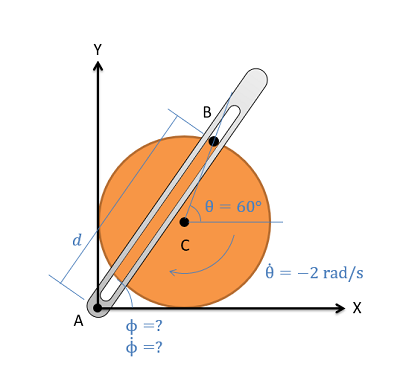
Un primer cuadrante de orientación estándar del plano cartesiano, con el origen centrado en el punto A. La vista lateral de una manivela está representada por un círculo que está centrado en el punto C en el primer cuadrante y tangente a los ejes x e y. El círculo gira en sentido horario a 2 rad/s. Una barra larga con una ranura cortada a través de ella tiene un extremo fijo en el punto A, y el pasador en el punto B en el borde exterior del círculo pasa a través de esta ranura. La distancia entre los puntos A y B se etiqueta como d. En la posición actual de B, la línea AB forma un ángulo de phi con el eje x y la línea BC hace un ángulo de theta = 60° por encima de la horizontal. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Una vista lateral circular de una manivela giratoria con un pasador en un borde. El pasador se mueve a través de una ranura en un extremo de una barra basculante, cuyo otro extremo está fijo en su lugar.

Solución: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/DydbOzigdpU.