11.4: Análisis de Movimiento Relativo

Última actualización
Guardar como PDF

Page ID: 83902

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El análisis de movimiento relativo es un método utilizado para analizar cuerpos sometidos a movimiento plano general. El movimiento plano general es el movimiento donde los cuerpos pueden trasladarse y rotar al mismo tiempo. Además del análisis de movimiento relativo, la alternativa es el análisis de movimiento absoluto. Cualquiera de los dos métodos se puede utilizar para cualquier problema general de movimiento plano, sin embargo, un método puede ser significativamente más fácil de aplicar en ciertas situaciones.

El análisis de movimiento absoluto requerirá cálculo y generalmente es más rápido para problemas simples y problemas donde solo se requieren las velocidades (y no aceleraciones). El análisis de movimiento relativo no requerirá cálculo, pero sí requiere el uso de múltiples sistemas de coordenadas y generalmente es más fácil de usar para problemas más complejos y problemas donde se están analizando velocidades y aceleraciones.

Utilización del análisis de movimiento relativo

Para iniciar nuestra discusión sobre el análisis de movimiento relativo, vamos a imaginar un brazo robótico simple como el de abajo. En este brazo, tenemos dos secciones de brazo de longitud fija, con motores que provocan rotaciones en la articulación A y la junta B.

AB, un segmento de brazo robótico de 2 metros de largo con su base siendo el punto A, se estira hacia arriba y hacia la derecha para formar un ángulo de theta con el eje x positivo de un plano cartesiano de orientación estándar con el origen centrado en el punto A. BC, un segmento de brazo robótico de 1.5 metros de largo, se conecta al extremo libre del segmento AB y se estira hacia arriba y hacia la derecha, haciendo un ángulo de phi con la horizontal. — Figura\(\PageIndex{1}\): Este brazo robótico tiene una base fija en A, y dos secciones de brazo de longitud fija (AB y BC) que se controlan mediante motores en las articulaciones A y B. El efector final del brazo robótico está en C.

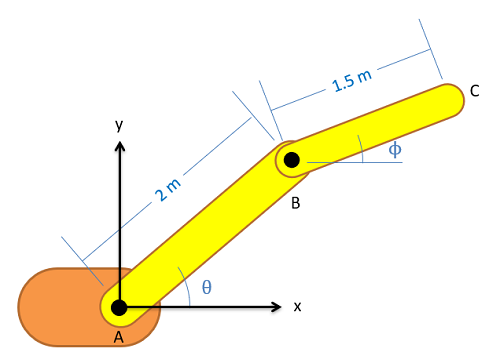
El primer paso en el análisis de movimiento relativo es descomponer el movimiento en pasos simples y asignar un sistema de coordenadas (con\(r\) y\(\theta\) direcciones) a cada paso de la cadena de movimiento. Siempre comenzaremos en un punto fijo y nos moveremos paso a paso a partir de ahí. En el caso de nuestro brazo robótico, la Articulación A es el único punto que no se va a mover así que empezamos ahí; entonces tenemos dos casos de rotación sin extensión a medida que avanzamos de A a B, luego B a C.

Dado que hay dos pasos para el movimiento, habrá dos sistemas de coordenadas. El primer sistema de coordenadas se unirá al miembro AB, con la\(r\) dirección que va del punto A al punto B. La\(\theta\) dirección será entonces noventa grados en sentido antihorario desde la\(r\) dirección. El segundo sistema de coordenadas se unirá al miembro BC, con la\(r\) dirección que va del punto B al punto C. Nuevamente, la\(\theta\) dirección es de noventa grados en sentido contrario a las agujas del reloj desde la\(r\) dirección. En este punto suele ser bueno identificar los ángulos de cada una de las\(\theta\) direcciones\(r\) y con respecto al suelo. A continuación se muestra una imagen del brazo robótico con ambos sistemas de coordenadas dibujados en.

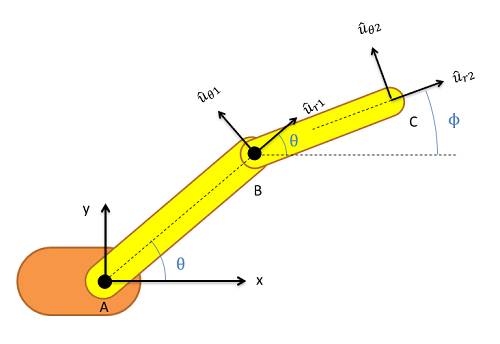
El brazo robótico de la Figura 1 anterior, con los dos nuevos sistemas de coordenadas dibujados en. El primer sistema de coordenadas tiene su origen ubicado en el punto B; su dirección r se extiende en la misma dirección que se mueve de A a B, y su dirección theta es 90° en sentido contrario a las agujas del reloj desde esa dirección r. El segundo sistema de coordenadas tiene su origen ubicado en el punto C; su dirección r se extiende en la misma dirección que se mueve de B a C, y su dirección theta es 90° en sentido contrario a las agujas del reloj desde esa dirección r. — Figura\(\PageIndex{2}\): Se utilizan dos sistemas de coordenadas en el análisis de movimiento relativo de este brazo robótico. El primer sistema de coordenadas está unido al miembro AB mientras que el segundo está unido al miembro BC. La\(r\) dirección siempre se alineará con los dos extremos del miembro, mientras que la\(\theta\) dirección siempre será 90° en sentido antihorario desde la\(r\) dirección correspondiente.

Para el análisis de movimiento relativo, podemos identificar la velocidad o aceleración del punto final del brazo (C) con respecto al suelo (A) encontrando la aceleración de velocidad de B con respecto a A y sumando la velocidad o aceleración de C con respecto a B, tal como hicimos con las partículas.

\ begin {align}\ text {Velocidad:}\ quad &\,\ vec {v} _ {C/A} =\ vec {v} _ {B/A} +\ vec {v} _ {C/B}\\ [4pt]\ text {Aceleración:}\ quad &\,\ vec {a} _ _ {C/A} =\ vec {a} _ {B/A} +\ vec {a} _ {B/C}\ end {align}

Las ecuaciones de análisis de movimiento relativo anteriores son para un movimiento de dos partes (ya que hay dos secciones al brazo en nuestro ejemplo), pero podemos expandir fácilmente la ecuación anterior en tres, cuatro o incluso más piezas para mecanismos más complejos agregando más pasos al lado izquierdo de nuestra ecuación.

Para utilizar las ecuaciones anteriores, necesitaremos enchufar la información que conocemos. Enchufar las velocidades o aceleraciones que se dan como parte del problema para cualquier punto en particular es un buen lugar para comenzar. Si se diera la velocidad de los puntos B o C, por ejemplo, la conectaríamos para\(\vec{v}_{B / A}\) o\(\vec{v}_{C / A}\) respectivamente. Recuerde que el punto A es nuestro punto fijo de tierra, así\(\vec{v}_{C / A}\) es la velocidad del punto C con respecto al suelo mientras que\(\vec{v}_{C / B}\) es la velocidad del punto C con respecto al punto B. Si algún punto es fijo (que no sea nuestro punto de tierra original, que siempre será fijo), también podemos enchufar ceros para ambos velocidad y aceleración de ese punto. Recuerde que esta ecuación es una ecuación vectorial, por lo que estas velocidades tienen tanto una magnitud como una dirección.

Para tener en cuenta la rotación o extensión de cualquier pieza individual, tendremos que mirar hacia atrás a nuestras ecuaciones cinemáticas para sistemas de coordinadores polares. A continuación se presentan las ecuaciones que teníamos para velocidad y aceleración.

\ begin {align}\ text {Velocidad:}\ quad &\, v =\ punto {r}\ hat {u} _r + r\ punto {\ theta}\ hat {u} _ {\ theta}\\ [4pt]\ text {Aceleración:}\ quad &\, a = (\ ddot {r} - r\ punto {\ theta} ^2)\ hat {u} _r + (2\ punto {r}\ punto {\ theta} + r\ ddot {\ theta})\ hat {u} _ {\ theta}\ end {align}

En las ecuaciones anteriores,\(r\) representa la longitud de la pieza de brazo respectiva (la longitud del miembro AB o BC),\(\dot{r}\) representa la velocidad a la que esa longitud está aumentando, y\(\ddot{r}\) representa la velocidad a la que esa tasa está aumentando. El\(\theta\) término representa el ángulo actual de la pieza de brazo,\(\dot{\theta}\) es la velocidad angular de esa pieza de brazo y\(\ddot{\theta}\) es la aceleración angular de esa pieza de brazo. Las\(u_{\theta}\) direcciones\(u_r\) y son las\(\theta\) direcciones\(r\) y que se adjuntan a esa sección particular del brazo (en nuestro dibujo anterior,\(\hat{u}_{r_1}\) y\(\hat{u}_{\theta_1}\) se adjuntaron al miembro AB y\(\hat{u}_{r_2}\) y\(\hat{u}_{\theta_2}\) se adjuntaron al miembro BC).

Aunque ciertamente es posible tener un mecanismo que gira y se extiende al mismo tiempo, a menudo tendremos ya sea una simple rotación, o simplemente una simple extensión a lo largo de una dirección fija. Con rotación simple, los\(\ddot{r}\) términos\(\dot{r}\) y son cero, y nuestras ecuaciones se reducen a lo siguiente.

\ begin {align}\ text {Velocidad:}\ quad &\, v = r\ punto {\ theta}\ hat {u} _ {\ theta}\\ [4pt]\ text {Aceleración:}\ quad &\, a = - r\ punto {\ theta} ^2\ hat {u} _ _ {r} + r\ ddot {\ theta}\ hat {u} _ {theta}\ end {align}

Si tenemos extensión simple, donde la longitud de la pieza está cambiando pero no hay rotación, los\(\ddot{\theta}\) términos\(\dot{\theta}\) y serían cero y nuestras ecuaciones originales se reducirían a lo siguiente.

\ begin {align}\ text {Velocidad:}\ quad &\, v =\ punto {r}\ hat {u} _r\\ texto {Aceleración:}\ quad &\, a =\ ddot {r}\ hat {u} _r\ end {align}

Si usamos el conjunto apropiado de ecuaciones para el tipo de movimiento en cada paso y conectamos cantidades conocidas para velocidades angulares, aceleraciones angulares y tasas o extensión para cada pieza, podemos agregar estas piezas a nuestra ecuación de análisis de movimiento relativo de antes. Nuevamente, estos son vectores así que asegúrate de indicar tanto las magnitudes como las direcciones cuando las pongamos en la ecuación.

Una vez que tengamos todo en nuestra ecuación vectorial, dividiremos la ecuación vectorial en\(x\) y\(y\) componentes para resolver cualquier incógnitas. Simplemente encuentre los ángulos o cada una de las\(\theta\) direcciones\(r\) y usando su diagrama y luego use senos y cosenos para descomponer los vectores individuales en\(x\) y\(y\) componentes. Una vez que tengas todo en forma de componente, deberías ser capaz de resolver cualquier incógnitas en tus ecuaciones. Como nota, a menudo es necesario comenzar con las ecuaciones de velocidad y resolver algunas incógnitas allí antes de pasar a las ecuaciones de aceleración.

Notación alternativa para el movimiento relativo del cuerpo rígido

En algunos casos, queremos analizar múltiples puntos en el mismo o varios cuerpos rígidos. Otra notación utilizada para esto es:

\ begin {align}\ text {Posición:}\ quad &\,\ vec {r} _B =\ vec {r} _A +\ vec {r} _ {B/A}\\ [5pt]\ text {Velocidad:}\ quad &\,\ vec {v} _B =\ vec {v} _A +\ vec {v} _ {B/A}\ vec {v} _A +\ vec {\ omega}\ veces\ vec {r} _ {B/A}\\ [5pt]\ text {Aceleración:}\ quad &\,\ vec {a} _B =\ vec {a} _A +\ vec {a} _ {B/A} =\ vec {a} _A +\ vec {\ alpha}\ times\ vec {r} _ {B/A} +\ vec {\ omega}\ times (\ vec {\ omega}\ times\ vec {r} _ _ {B/A})\ end {align} En esta notación, A y B son dos puntos en un mismo cuerpo rígido. Cuando usamos solo un subíndice, eso indica la posición/velocidad/aceleración de ese punto con respecto al sistema de coordenadas fijas. Debido a que el cuerpo es rígido, los dos puntos no cambiarán la distancia entre ellos, pero el vector de posición entre ellos puede cambiar la orientación (que es de donde proviene la velocidad relativa entre los dos puntos). \(\vec{\omega}\)es la velocidad angular de ese cuerpo rígido (análoga a\(\dot{\theta}\)), y\(\vec{\alpha}\) es la aceleración angular de ese cuerpo rígido (análoga a\(\ddot{\theta}\)).

Para el movimiento plano, donde el vector de velocidad angular (fuera del plano) siempre es perpendicular al vector de posición (en el plano), la aceleración se puede simplificar para:

\[ \text{Acceleration:} \quad \, \vec{a}_B = \vec{a}_A + \vec{\alpha} \times \vec{r}_{B / A} - \omega^2 \vec{r}_{B / A} \]

Mismo diagrama que en la Figura 1 anterior: AB, un segmento de brazo robótico de 2 metros de largo con su base siendo el punto A, se estira hacia arriba y hacia la derecha para formar un ángulo de theta con el eje x positivo de un plano cartesiano de orientación estándar con el origen centrado en el punto A. BC, un segmento de brazo robótico de 1.5 metros de largo, se conecta a el extremo libre del segmento AB y se estira hacia arriba y hacia la derecha, haciendo un ángulo de phi con la horizontal. — Figura\(\PageIndex{1}\), este brazo robótico tiene una base fija en A, y dos secciones de brazo de longitud fija (AB y BC) que se controlan mediante motores en las articulaciones A y B. El efector final del brazo robótico está en C.

Si consideramos el mismo brazo robótico, podemos traducir nuestra notación anterior a la nueva notación de cuerpo rígido:

\ begin {align}\ punto {\ theta}\ sombrero {k} &=\ vec {\ omega} _ {AB}\\ [4pt]\ punto {\ phi}\ sombrero {k} &=\ vec {\ omega} _ {BC}\\ [4pt]\ ddot {\ theta}\ sombrero {k} &=\ vec {\ alfa} _ {AB}\ [4pt]\ ddot {\ phi}\ hat {k} &=\ vec {\ alpha} _ {BC}\ end {align}

Todos los vectores se definirán con respecto a las\(y\) coordenadas\(x\) y en el sistema de coordenadas mostrado, en lugar de las direcciones radial y theta como arriba.

Si queremos encontrar la velocidad y aceleración del punto final, C, conociendo las velocidades angulares y aceleraciones, encontraremos las siguientes relaciones:

\ begin {align}\ text {Velocidad en el punto B:}\ quad &\,\ vec {v} _B =\ vec {v} _A +\ vec {\ omega}\ veces\ vec {r} _ {B/A}\\ [5pt]\ text {Velocidad en el punto C:}\ quad &\,\ vec {v} _C =\ vec {v} _B +\ vec {\ omega}\ veces\ vec {r} _ {C/B} =\ vec {v} _A +\ vec {\ omega}\ veces\ vec {r} _ {B/A} +\ vec {\ omega}\ veces\ vec {r} _ {C/B} \\ [5pt]\ text {Aceleración en el punto B:}\ quad &\,\ vec {a} _B =\ vec {a} _A +\ vec {\ alpha}\ veces\ vec {r} _ {B/A} -\ omega^2\ vec {r} _ {B/A}\\ [5pt]\ text {Aceleración en el punto C:}\ &\,\ vec {a} _C =\ vec {a} _B +\ vec {\ alfa}\ veces\ vec {r} _ {C/B} -\ omega^2\ vec {r} _ {C/B} =\ vec {a} _A +\ vec {\ alfa}\ tiempos\ vec {r} _ {B/A} -\ omega^2\ vec {r} _ {B/A} +\ vec {\ alfa}\ veces\ vec {r} _ {C/B} -\ omega^2\ vec {r} _ {C/B}\ end {align}

Videoconferencia que cubre este capítulo, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/6qAY9iB9xi0.

Ejemplo\(\PageIndex{1}\)

El brazo robótico que se muestra a continuación tiene una base naranja fija en A y miembros de longitud fija AB y BC. Los motores en A y B permiten el movimiento de rotación en las juntas. Con base en las velocidades angulares y aceleraciones mostradas en cada articulación, determinar la velocidad y la aceleración del efector final en C.

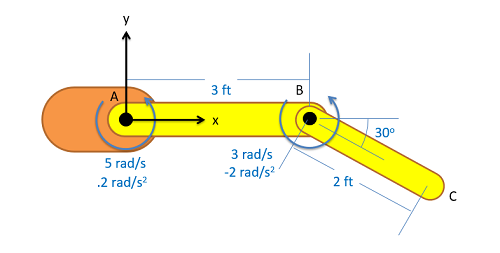
Un miembro horizontal AB de 3 pies de largo está fijado a una base inmóvil en su extremo izquierdo, punto A. Un motor en el punto A proporciona una rotación en sentido contrario a las agujas del reloj de 5 rad/s y 0.2 rad/s². Un miembro de 2 pies de largo, BC, se estira hacia abajo y hacia la derecha desde el punto final derecho del miembro AB, a 30° por debajo de la horizontal. Un motor en el punto B proporciona una rotación en sentido contrario a las agujas del reloj de 3 rad/s y -2 rad/s². — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un brazo robótico con dos segmentos tiene motores en sus articulaciones, que giran a velocidades y aceleraciones conocidas.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/fOjS1O2-3LQ.

Ejemplo\(\PageIndex{2}\)

El brazo robótico del problema anterior se encuentra en la configuración que se muestra a continuación. Supongamos que actualmente\(\theta\) es de 30 grados y que el punto C actualmente se encuentra a lo largo del\(x\) eje. Si queremos que el efector final en C viaje 1 pies/s en la\(x\) dirección negativa, ¿cuáles deberían ser las velocidades angulares en las juntas A y B?

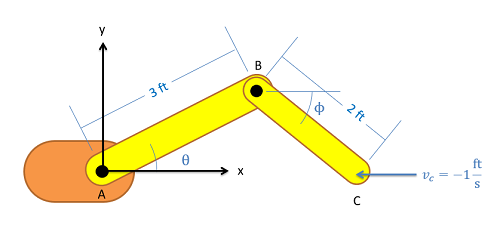
El miembro AB de 3 pies de largo tiene su punto final izquierdo, A, unido a una base fija y se estira hacia arriba y hacia la derecha, formando un ángulo de theta por encima de la horizontal. Un plano cartesiano de orientación estándar se centra en el punto A. El miembro BC de 2 pies de largo se extiende hacia abajo y hacia la derecha desde el extremo libre de AB, en un ángulo de phi debajo de la horizontal. El efector final en el punto C, el extremo libre del miembro BC, se mueve horizontalmente hacia la izquierda a 1 pies/s (en la dirección x negativa). — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un brazo robótico de dos segmentos tiene un efector en su extremo libre que se mueve a una velocidad conocida, como resultado de la rotación de los motores en las dos juntas.

Solución: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/esp_gz8VKRs.

Ejemplo\(\PageIndex{3}\)

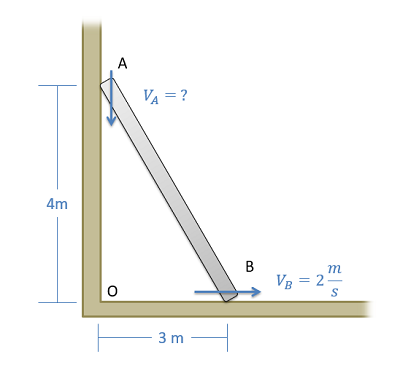
Una escalera está apuntalada contra una pared como se muestra a continuación. Si la base de la escalera se desliza a una velocidad de 2 m/s, ¿cuál es la velocidad de la parte superior de la escalera?

Vista lateral de una pared y una escalera apuntalada contra el lado derecho de esa pared. El extremo de la escalera en la pared, A, está a 4 pies sobre el piso. El extremo de la escalera en el piso, B, está a 3 pies a la derecha de la pared y se desliza hacia la derecha a 2 m/s. El punto de intersección entre la pared y el piso está etiquetado como punto O. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Una escalera apuntalada contra una pared está cayendo, ya que su pie se desliza alejándose de la pared.

Solución: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/SzAq3HD7qJY.

Ejemplo\(\PageIndex{4}\)

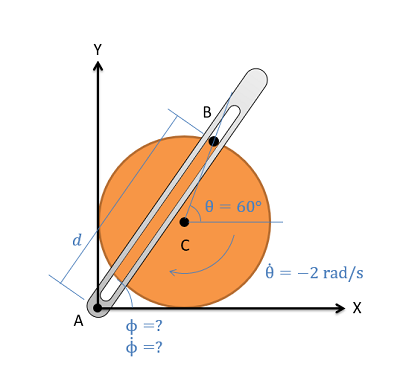
El mecanismo biela-balancín como se muestra a continuación consiste en una manivela con un radio de 0.5 metros que gira alrededor de su centro fijo en C, a una velocidad constante de 2 rad/s en sentido horario. El balancín AB se fija en su base en A y se conecta al punto B a lo largo del borde de la manivela. El pasador en el punto B puede deslizarse a lo largo de una ranura sin fricción en AB. En su estado actual, ¿cuál es la velocidad angular del balancín AB?

Un primer cuadrante de orientación estándar del plano cartesiano, con el origen centrado en el punto A. La vista lateral de una manivela está representada por un círculo que está centrado en el punto C en el primer cuadrante y tangente a los ejes x e y. El círculo gira en sentido horario a 2 rad/s. Una barra larga con una ranura cortada a través de ella tiene un extremo fijo en el punto A, y el pasador en el punto B en el borde exterior del círculo pasa a través de esta ranura. La distancia entre los puntos A y B se etiqueta como d. En la posición actual de B, la línea AB forma un ángulo de phi con el eje x y la línea BC hace un ángulo de theta = 60° por encima de la horizontal. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Una vista lateral circular de una manivela giratoria con un pasador en un borde. El pasador se mueve a través de una ranura en un extremo de una barra basculante, cuyo otro extremo está fijo en su lugar.

Solución: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/Exys74nj02I.