11.5: Análisis de Marco Giratorio

Última actualización
Guardar como PDF

Page ID: 83907

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El análisis de marco giratorio es una parte especializada del análisis de movimiento relativo. Se realiza típicamente en coordenadas cartesianas (\(x\)-\(y\)) para cuerpos rígidos. En la sección anterior, se utilizaron marcos rotativos en coordenadas polares para resolver problemas con fórmulas similares a las de la cinemática de partículas. Adoptaremos una notación ligeramente diferente que está especializada en cuerpos rígidos. Estas fórmulas son las fórmulas de cinemática plana más generales, es decir, siempre se pueden usar, y proporcionarán la respuesta correcta. Sin embargo, son innecesariamente complicados para muchos tipos de movimiento, como la rotación pura.

El análisis de marco giratorio es realmente importante para los casos en los que los objetos no están fijados entre sí. ¿Cuándo se utilizan marcos giratorios? Cuando un objeto se desliza contra otro objeto, o dos objetos ni siquiera están en contacto, pero se quiere saber algo sobre la relación de movimiento entre ellos y/o se les da información sobre la relación de movimiento entre ellos.

Marcos de Referencia:

En la mayor parte del material anterior, se ha trabajado con el marco\(O_{xyz}\) de referencia fijo y un marco de referencia de traslación (pero no giratorio) unido al cuerpo rígido en un punto\(A\), marco\(A_{xyz}\).

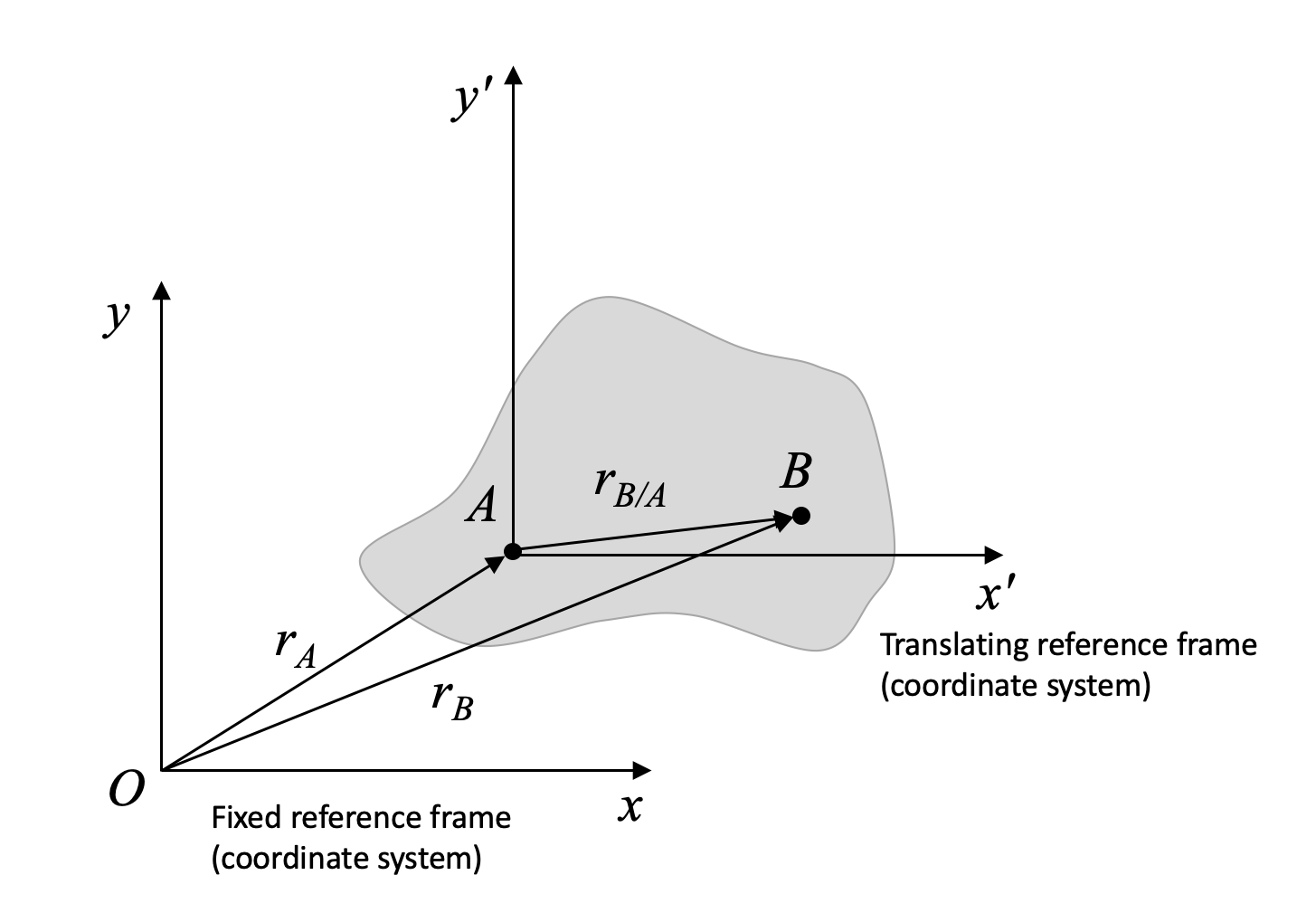
Plano de coordenadas cartesianas fijo, con el origen en el punto O en la esquina inferior izquierda. Un objeto se mueve a través del primer cuadrante de ese plano, con el vector R_a apuntando del punto O al punto A en el objeto y R_b apuntando del punto O al punto B en el objeto. Otro sistema de coordenadas está viajando en el mismo marco de referencia que el objeto: se muestra en una orientación estándar con su origen en el punto A, siendo su dirección horizontal x' (x-prime) y su dirección vertical siendo y' (y-prime). — Figura\(\PageIndex{1}\): Un cuerpo rígido con un marco de referencia de traslación (no giratorio)\(x'y'z'\) unido en un punto\(A\), con relación al marco fijo\(xyz\) en\(O\).

Esto nos ha dado ecuaciones de movimiento relativo:

\ begin {align}\ text {Posición:}\ quad &\,\ vec {r} _ {B/O} =\ vec {r} _ {A/O} +\ vec {r} _ {B/A}\\ text {Velocidad:}\ quad &\,\ vec {v} _ _ {B/O} =\ vec {v} _ {A/O} +\ vec {v} _ {B/A} =\ vec {v} _ {A/O} +\ vec {\ omega}\ veces\ vec {r} _ {B/A}\\ text {Aceleración:}\ quad &\,\ vec {a} _ {B/O} =\ vec {a} _ {A/O} +\ vec {a} _ {B/A} =\ vec {a} _ {A/O} +\ vec {\ alfa}\ veces\ vec {r} _ {B/A} -\ omega^2\ vec {r} _ {B/A}\ end {align}

Tenga en cuenta que la notación\(r_{B / O}\), donde\(O\) está el marco fijo, también se puede escribir como\(r_B\). Ambos indican una posición absoluta (o velocidad o aceleración), es decir, un valor con respecto al cuadro fijo\(O\).

Marcos giratorios:

Ahora, consideraremos un marco de referencia que se une a un punto en el cuerpo rígido y que gira y traslada con el cuerpo rígido. Introduciremos algunos términos adicionales para dar cuenta de la rotación del marco.

Considera un cuerpo rígido con marco\(x'y'z'\) en el punto\(A\). \(x'y'z'\)se mueve y gira con el cuerpo. Un bicho,\(B\), se arrastra a lo largo del cuerpo.

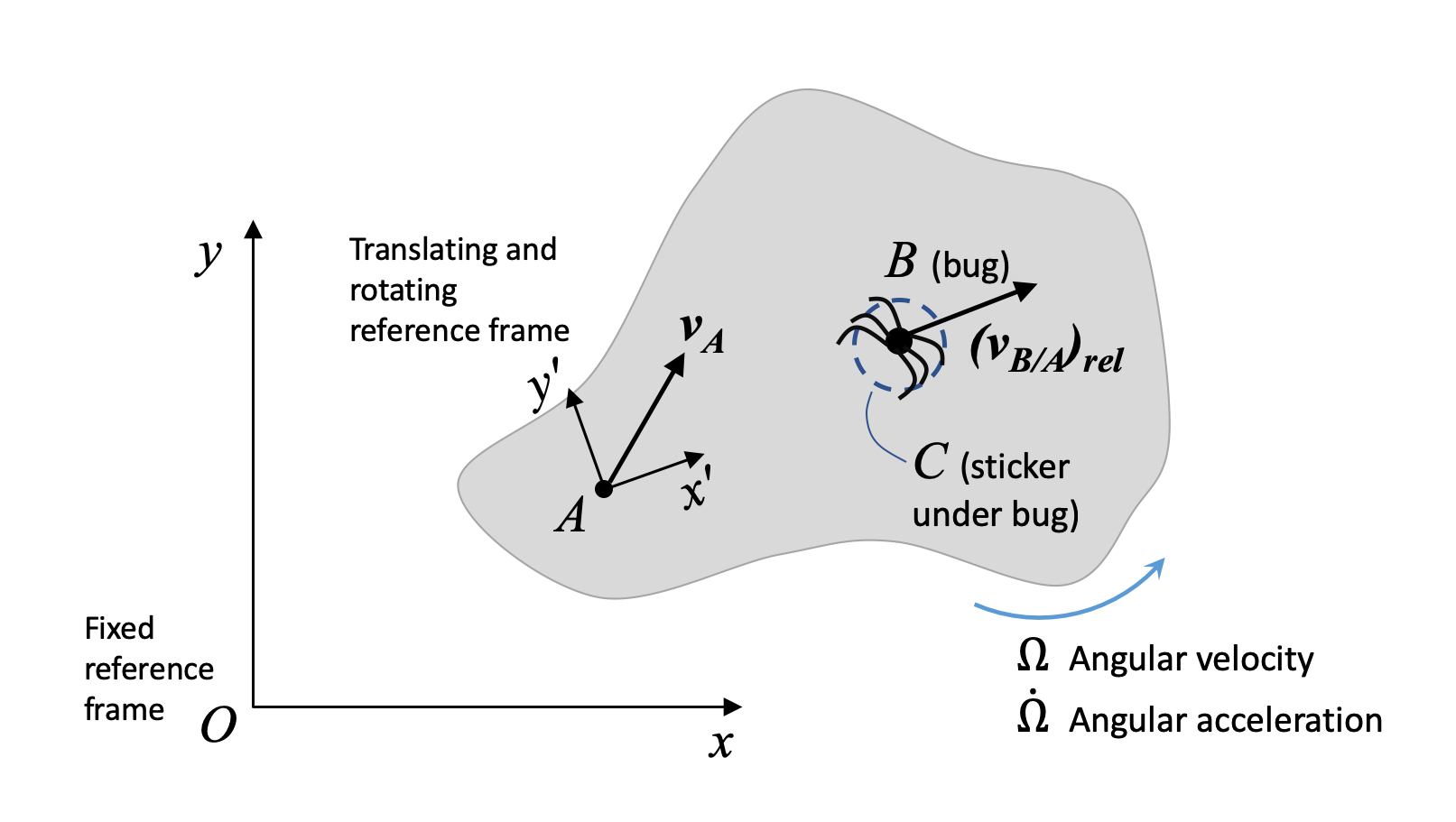
Plano cartesiano fijo de orientación estándar con el origen en el punto O, en la parte inferior izquierda de la imagen. Un cuerpo rígido se mueve a través del primer cuadrante de ese plano, experimentando tanto traslación como rotación (a cierta velocidad angular Omega). Otro sistema de coordenadas, con ejes x' e y', tiene su origen en el punto A del cuerpo, y se traduce y gira con el cuerpo. Un insecto se arrastra sobre el cuerpo, y el punto B es la posición instantánea del error. En el instante que se muestra, el error está encima de una pegatina redonda, punto C, que está fijada al cuerpo rígido. — Figura\(\PageIndex{2}\): Un cuerpo rígido con un marco de referencia de traslación Y giratorio\(x'y'z'\), unido en el punto\(A\). Un insecto,\(B\), se arrastra a lo largo del cuerpo rígido, con una velocidad relativa al marco giratorio. El error se encuentra actualmente por encima de una pegatina\(C\),, que se fija rígidamente al cuerpo rígido.

Para un observador sentado en\(A\), el bicho parece estar arrastrándose en línea recta. Pero para un observador sentado\(O\), el bicho no parece que se esté moviendo en línea recta, porque el cuerpo sobre el que se arrastra también se mueve (traslada y gira). Nos gustaría describir el movimiento del error visto por un observador en\(O\). Para recordarnos que estamos tratando con un marco giratorio unido a un cuerpo, utilizamos omega mayúscula\(\Omega\)) para denotar la velocidad angular del objeto al que está unido el marco giratorio, y\(\dot{\Omega}\) para la aceleración angular del objeto con el marco giratorio unido. Finalmente, utilizamos corchetes y el subíndice\(rel\) para denotar valores de velocidad o aceleración expresados con respecto al marco giratorio.

Recordemos que los vectores tienen tanto magnitud como dirección. Podemos expresar un vector en componentes con respecto a los vectores\(\hat{i}\) y\(\hat{j}\) unitarios:

\[ \vec{r}_{B / O} = r_{B/O, x} \hat{i} + r_{B/O, y} \hat{j} \]

Normalmente, cuando tomamos una derivada temporal de tal expresión, la longitud del vector (es decir, los\(r_{B/O, y}\) términos\(r_{B/O, x}\) y) cambia, pero los vectores unitarios no. En el caso del marco giratorio, los vectores unitarios cambian. Ahora, no cambian de longitud, siguen siendo vectores unitarios. Pero están unidos a un cuerpo giratorio, lo que significa que también giran. Es decir, sus direcciones cambian, y tenemos que dar cuenta de eso al derivar expresiones de velocidad y aceleración.

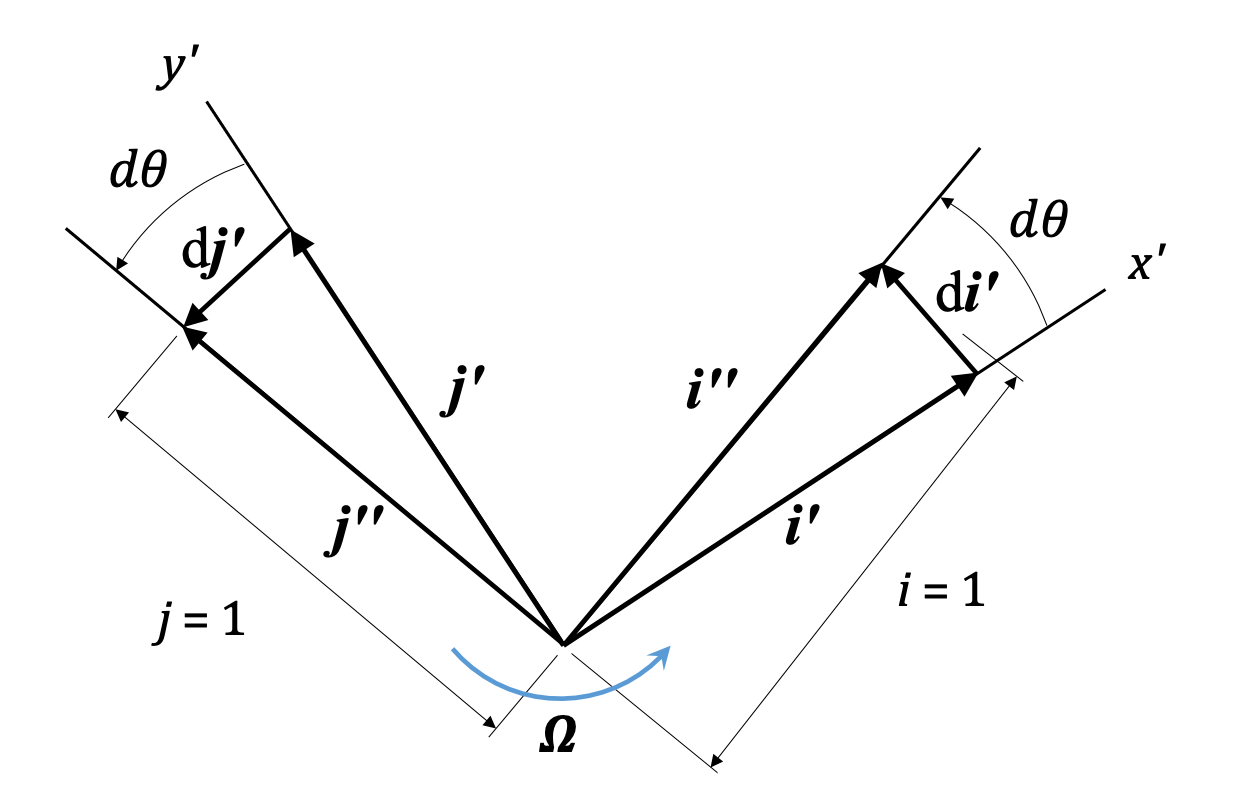
Un sistema de coordenadas con su origen en cierto punto de un cuerpo en movimiento gira a medida que gira el cuerpo. A medida que el cuerpo gira en sentido antihorario una pequeña cantidad d theta, cambia la dirección en la que apuntan los vectores unitarios: j' se convierte en j”, que apunta más hacia la izquierda y menos bruscamente hacia arriba; i' se convierte en i”, que apunta más bruscamente hacia arriba y menos hacia la derecha. Las longitudes de los vectores unitarios permanecen 1, y el ángulo entre ellos permanece 90°. — Figura\(\PageIndex{3}\): Cuando el marco de referencia gira con el cuerpo rígido giratorio, los vectores unitarios cambian con el tiempo.

Se puede ver que obtenemos pequeños vectores\(d \hat{i'}\) y\(d \hat{j'}\) que describen el cambio de dirección de los vectores unitarios, y la magnitud de ese cambio está directamente relacionada con\(\Omega\), la velocidad angular del cuerpo rígido y el marco giratorio.

\[ \frac{d \hat{i'}}{dt} = \Omega \hat{k} \times \hat{i'} = \Omega \hat{j'} \]

\[ \frac{d \hat{j'}}{dt} = \Omega \hat{k} \times \hat{j'} = -\Omega \hat{i'} \]

Cuando diferenciamos la posición relativa del error\(B\), con respecto al marco giratorio\(A\), tenemos:

\[\frac{d \vec{r}_{B/A}}{dt} = \left( \dot{r}_{B/A, \ x'} \ \hat{i'} + \dot{r}_{B/A, \ y'} \ \hat{j'} \right) + \vec{\Omega} \times \left( r_{B/A, \ x'} \ \hat{i'} + r_{B/A, \ y'} \hat{j'} \ \right) \]

\ begin {align}\ text {Nuevo término:}\ quad &\,\ left (\ dot {r} _ _ {B/A,\ x'}\\ hat {i'} +\ dot {r} _ {B/A,\ y'}\ hat {j'}\ right) =\ left (\ vec {v} _ _ {B/A}\ right) _ {rel}\\ text {Igual que antes:}\ quad &\,\ vec {\ Omega}\ veces\ izquierda (r_ {B/A,\ x'}\\ sombrero {i'} + r_ {B/A,\ y'}\ sombrero {j'}\ derecha) =\ vec {\ Omega}\ veces\ vec {r} _ {B/A}\ end {align}

El nuevo término anterior describe el movimiento del error debido a la rotación del cuerpo rígido (y el\(x'y'z'\) marco), mientras que el término familiar anterior describe el movimiento del error visto por un observador fijado a\(x'y'z'\). Nuestra expresión final para la velocidad del error con respecto al fotograma fijo es:

\[ \vec{v}_{B/O} = \vec{v}_{A/O} + \vec{\Omega} \times \vec{r}_{B/A} + ( \vec{v}_{B/A} )_{rel} \]

Esta expresión final tiene el nuevo término\( (\vec{v}_{B/A})_{rel} \),, que describe el movimiento del error visto desde el marco giratorio. Se puede notar que si el error no se mueve,\( (\vec{v}_{B/A})_{rel} = 0\), y obtenemos la expresión familiar de los marcos traducibles, no giratorios. Así, esta expresión es la expresión de velocidad relativa más general.

De manera similar, podemos derivar una ecuación de aceleración diferenciando la ecuación de velocidad anterior. La expresión final es:

\[ \vec{a}_{B/O} = \vec{a}_{A/O} + \dot{\vec{\Omega}} \times \vec{r}_{B/A} + \vec{\Omega} \times ( \vec{\Omega} \times \vec{r}_{B/A} ) + 2 \vec{\Omega} \times (\vec{v}_{B/A})_{rel} + (\vec{a}_{B/A})_{rel} \]

Tabla\(\PageIndex{1}\): Correspondencias físicas de los\(\PageIndex{11}\) componentes de la ecuación
Movimiento del marco giratorio unido al cuerpo rígido:	\( \vec{a}_{A/O} + \dot{\vec{\Omega}} \times \vec{r}_{B/A} + \vec{\Omega} \times ( \vec{\Omega} \times \vec{r}_{B/A} ) \)
Aceleración de Coriolis - interacción del movimiento del objeto con respecto al marco giratorio y el movimiento del marco giratorio:	\( 2 \vec{\Omega} \times (\vec{v}_{B/A})_{rel} \)
Movimiento del objeto con respecto al marco giratorio:	\( ( \vec{a}_{B/A} )_{rel} \)

Tenga en cuenta que, para el movimiento plano (2D):

\[ \vec{\Omega} \times ( \vec{\Omega} \times \vec{r}_{B/A} ) = - \Omega^2 \vec{r}_{B/A} \]

Nuevamente, si el error se queda quieto, ambos\(rel\) términos se vuelven cero (no se mueve con respecto al cuerpo rígido), y nos quedamos con la misma expresión de movimiento relativo que se usa con los marcos de traducción. Entonces, Ecuación\(\PageIndex{11}\) es la forma más general de la ecuación de aceleración relativa y siempre se puede utilizar.

Al abordar estos problemas, hay varias cosas importantes para recordar:

Debe elegir el cuerpo correcto para unir el marco giratorio. El cuerpo correcto tendrá otro cuerpo deslizándose contra él. Si el objeto de interés está fijado al cuerpo que elegiste, puede que no sea correcto.
A menudo es útil alinear su marco giratorio de tal manera que termine con un ""\(rel\) "término o términos simplificados. Por ejemplo, alinee el\(x'\) eje con la dirección de movimiento del error, de modo que\( (\vec{v}_{B/A})_{rel} \) esté en la\(x'\) dirección -dirección.
Los componentes de todos los términos de cualquier ecuación deben calcularse a lo largo de la misma\(\hat{i}\) y\(\hat{j}\) direcciones. Si los marcos no están alineados, debe elegir UN FRAME y expresar todos los términos a lo largo de que las direcciones del ONE FRAME. (Es posible que puedas cambiar entre fotogramas en diferentes ecuaciones, ¡pero asegúrate de tener cuidado con la notación!)
Cuando se le da información en un problema, preste atención cuidadosa a qué marco se está refiriendo.
¡Asegúrate de incluir todos los términos en la ecuación de aceleración! Es fácil perderse uno. Deberías tener cinco términos.

Estos son algunos de los problemas más complejos de la cinemática plana, ¡así que tómate tu tiempo!

Ejercicio\(\PageIndex{1}\)

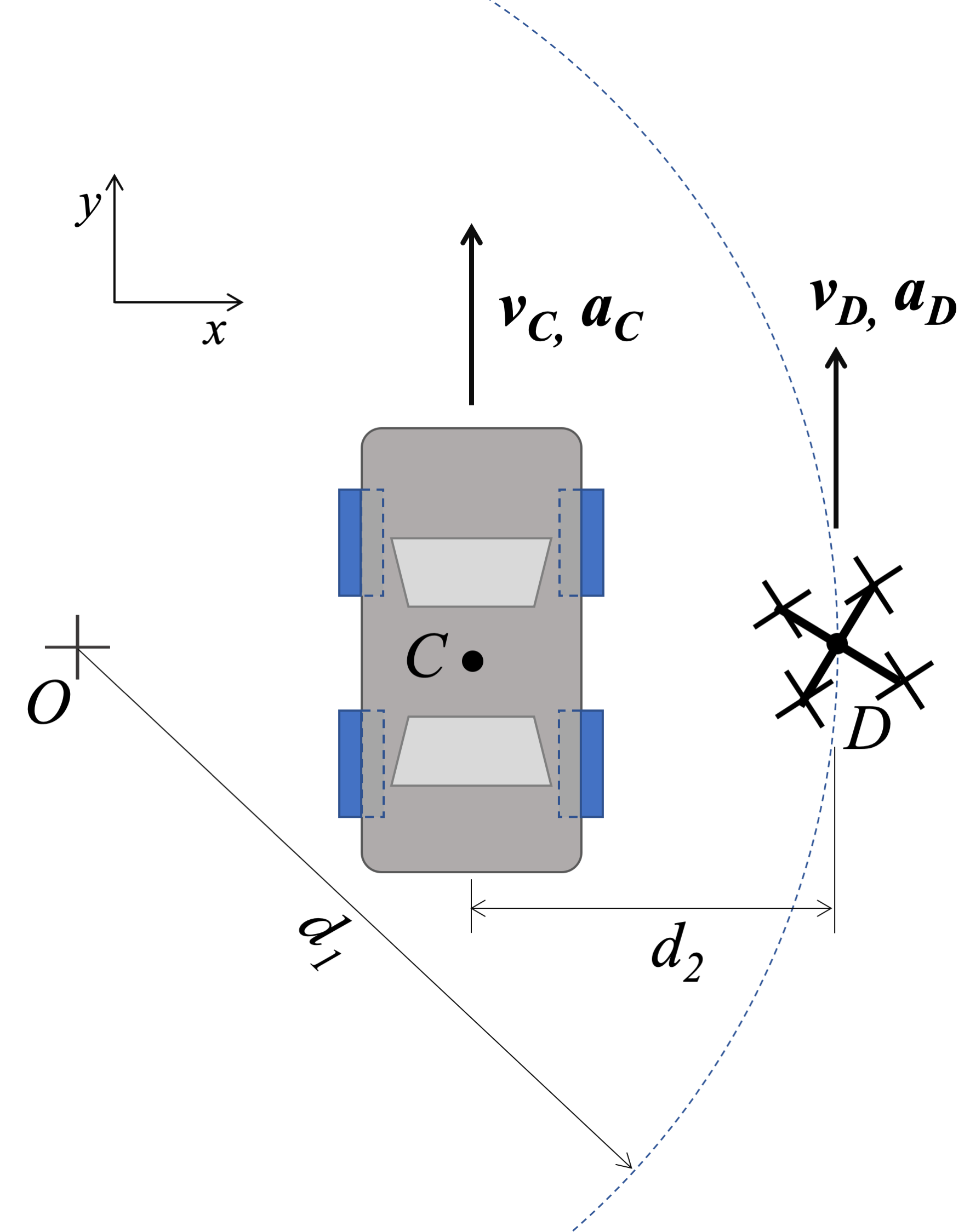
Un dron con cámara,\(D\), vuela sobre una carrera de autos en una trayectoria curva (centro\(O\)) con una velocidad constante de tierra de\(v_D = 9 \ m/s\). En el momento que se muestra,\(C\) el automóvil viaja con velocidad de\(v_c = 12 \ m/s\) y una aceleración de\(a_c = 2 \ m/s^2\) como se muestra. Supongamos\(d_1 = 7.5 \ m, \ d_2\) =\ 3 m\).

Encuentra la velocidad del auto tal como la observa la cámara en el dron D en este instante.
Encuentra en este instante la aceleración del auto observada por la cámara en el dron D.

Un punto fijo O se ubica en el lado izquierdo del diagrama, centrado verticalmente. Un dron ha recorrido la distancia d1 a la derecha y hacia abajo desde O antes de comenzar a volar en una trayectoria curva que forma un arco de círculo centrado en O. Actualmente la ubicación D del dron está directamente a la derecha de O, sus vectores de velocidad y aceleración apuntando directamente hacia la parte superior del diagrama. La ubicación de un automóvil, el punto C, se encuentra actualmente a una distancia d2 a la izquierda del punto D; los vectores de velocidad y aceleración del automóvil también son verticales y apuntan a la parte superior del diagrama. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un dron que traza una trayectoria circular alrededor del punto\(O\) se encuentra actualmente recto a la derecha de un automóvil, con los vectores de velocidad y aceleración de los dos vehículos apuntando en la misma dirección.

Solución: Video\(\PageIndex{1}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/nqs7bLBVm3g.

Ejemplo\(\PageIndex{2}\)

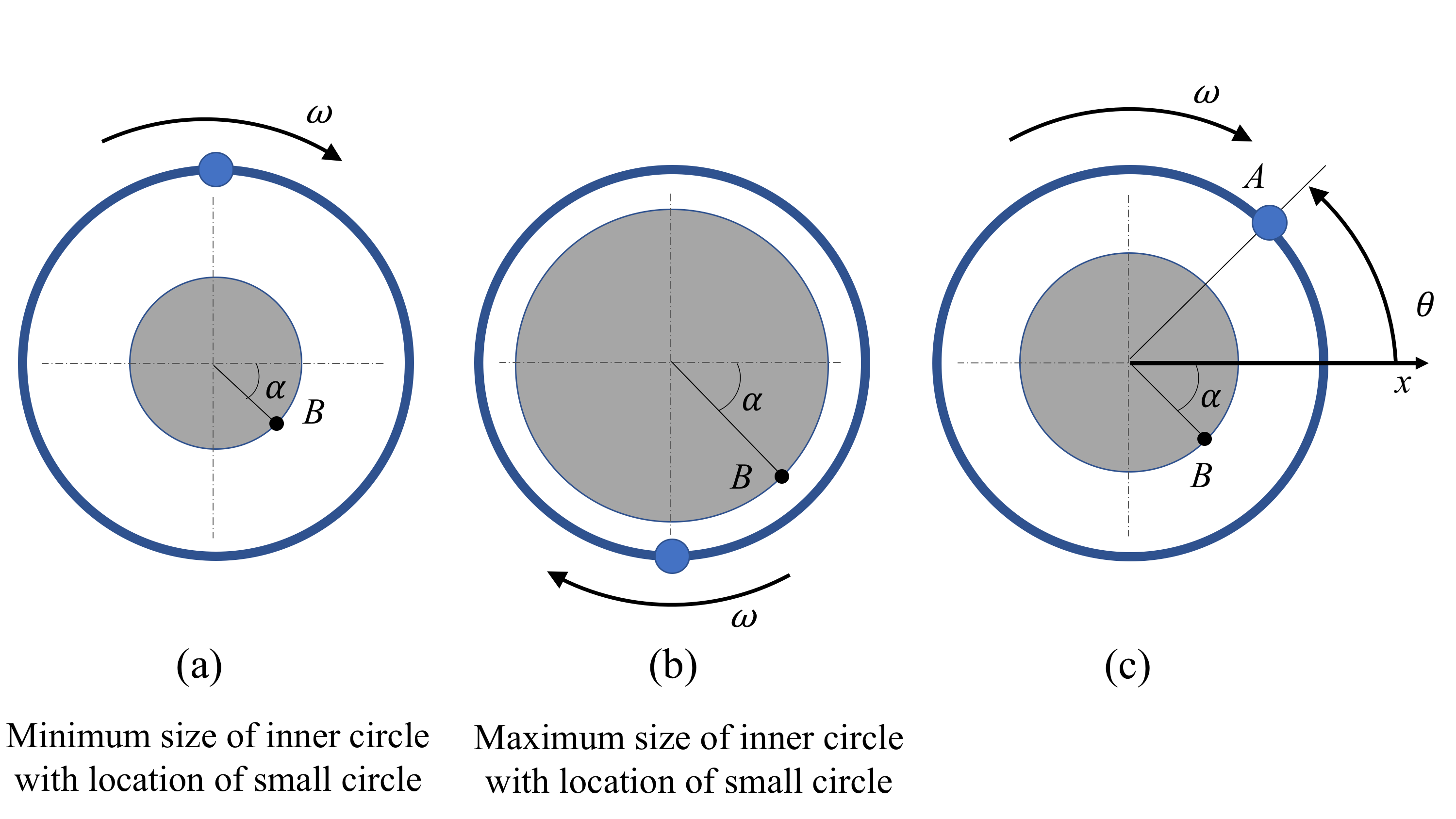
Un gráfico de video de ejercicio de respiración (algo similar a este) muestra un pequeño círculo moviéndose en una trayectoria circular restringida (radio constante 80 cm) a una velocidad angular constante de 0.4 rad/s alrededor de un círculo interno en expansión y contracción. El círculo interno se expande y contrae sinusoidalmente, desde un radio mínimo de 30 cm hasta un radio máximo de 60 cm. La distancia desde el centro del círculo interno hasta un punto en el borde del círculo interno puede ser descrita por la ecuación\(r = 0.45 - 0.15 \sin (\theta)\), donde\(r\) está en metros y\(\theta\) es la posición del círculo pequeño (cero en el\(x\) eje -eje).

Encuentre la velocidad y aceleración del punto B en el borde del círculo interno tal como lo ve un observador en el círculo pequeño en el punto\(A\) (vea la parte C de la figura a continuación). \(\theta = 45\)°,\(\alpha = 45\)°

A la izquierda, la Parte A muestra un círculo gris de tamaño mediano concéntrico con un contorno de círculo azul más grande. Los ejes x e y de un plano cartesiano de orientación estándar se ubican con su origen en el centro común de estos círculos. El contorno circular azul gira en sentido horario a una velocidad omega, moviendo un pequeño círculo azul unido al contorno. Actualmente este pequeño círculo azul se encuentra en el eje y positivo del sistema de coordenadas. El punto B se encuentra en el borde exterior del círculo gris, ubicado en un ángulo alfa por debajo del eje x positivo. La parte A está subtitulada “Tamaño mínimo del círculo interno con ubicación de círculo pequeño”. En el centro, la Parte B muestra el mismo círculo azul y sistema de coordenadas, pero el pequeño círculo azul ahora está en el eje y negativo y el círculo gris interior ha aumentado en radio. La parte B todavía se encuentra en el borde exterior del círculo gris, en el mismo ángulo alfa por debajo del eje x. La parte B está subtitulada “Tamaño máximo del círculo interno con ubicación de círculo pequeño”. A la derecha, la Parte C muestra el mismo círculo azul y sistema de coordenadas, pero el pequeño círculo azul (ahora etiquetado como A) está en el primer cuadrante en un ángulo de theta por encima del eje x. El círculo gris está en un tamaño entre sus tamaños en las partes A y B, con el punto B aún estando en su borde exterior en el mismo ángulo alfa debajo del eje x. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un contorno circular grande gira a una velocidad constante, cambiando la ubicación de un pequeño círculo unido a él, mientras que un círculo interior concéntrico con el contorno se expande y se contrae en radio.

Solución: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/mL0PVJNnOBE.