15.3: Vibraciones libres amortiguadas por fricción (Coulomb)

Última actualización
Guardar como PDF

Page ID: 84064

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La fricción también puede proporcionar amortiguación de vibraciones. En este caso, sin embargo, la amortiguación no es proporcional a la magnitud de la velocidad. Sólo depende de la dirección de la velocidad.

Recordamos de la sección sobre fricción seca que la fuerza de fricción en el deslizamiento depende únicamente del coeficiente de fricción cinética,\(\mu_k\), y la fuerza normal,\(F_N\).

\[ F_f = \mu_k F_N \]

La ecuación anterior no incluye la velocidad. Sabemos que la fricción cinética actúa para oponerse al movimiento, sin embargo, por lo que una expresión más completa sería:

\[F_f = - \text{sgn} (\dot{x}) \mu_k F_N , \]

donde\(sgn\) está la función “signo”, una función que captura el signo (dirección) de la velocidad. La ecuación anterior indica entonces que la dirección de fricción siempre es opuesta a la dirección de la velocidad, pero la magnitud de la velocidad no hace diferencia en la magnitud de la fricción.

La ecuación de movimiento del sistema se convierte en:

\[ m \ddot{x} + \mu m g \ \text{sgn} (\dot{x}) + kx = 0, \]

y la solución a esta ecuación de movimiento es:

\[ x(t) = \left( x_0 - \frac{(2n-1) \mu m g}{k} \right) \cos (\omega_n t) + \frac{\mu m g}{k} (-1)^{n+1} . \]

Si trazamos la respuesta, podemos ver que existen varias diferencias con respecto a un sistema con amortiguación viscosa.

Gráfico de la respuesta de amortiguación por fricción, con eje horizontal t y eje vertical x (t). A t = 0 la gráfica comienza en un valor positivo de x (t), y procede a oscilar alrededor del eje t con la amplitud decreciente gradualmente. Finalmente, en uno de los picos/puntos de respuesta de la gráfica, la fuerza del resorte de x (t) *k es menor que el valor necesario para superar la fricción estática y la posición x (t) ya no cambia con el tiempo. — Figura\(\PageIndex{1}\): Respuesta del sistema en amortiguamiento por fricción.

Algunas diferencias en comparación con la amortiguación viscosa incluyen:

El sistema oscila a la frecuencia natural del sistema, no a una frecuencia natural amortiguada.
Las curvas delimitadoras son lineales, no exponenciales.
El sistema no vuelve a cero. Esto se debe a que la magnitud de la fuerza de fricción no disminuye a medida que se reduce la amplitud del sistema, y en algún momento la fuerza del resorte ya no es capaz de superar la fricción estática que experimenta el sistema cuando cambia de dirección (\(v=0\)).

Comparación con el sistema viscoso de humedad insuficiente

Si consideramos nuestro sencillo sistema lineal de masa-resorte, la magnitud de\(F_f\) no cambia con la velocidad, a diferencia de la amortiguación viscosa. Si trazamos ambos tipos de amortiguamiento para un mismo sistema, obtendríamos lo siguiente:

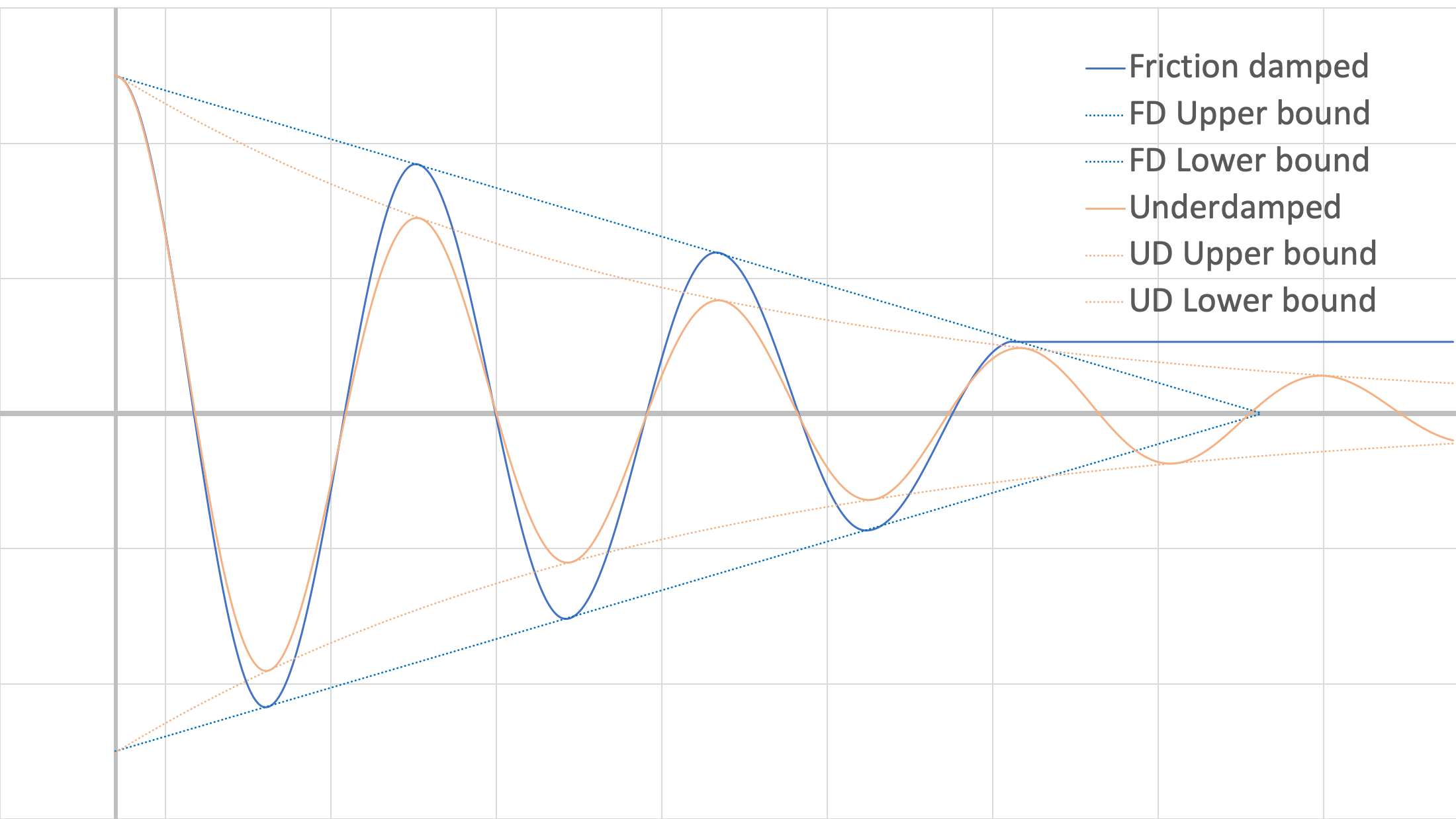
Gráfica de las respuestas viscosas y amortiguadas por fricción de un sistema masa-resorte. Ambas gráficas oscilan alrededor del eje t con amplitud en descomposición. Los límites superior e inferior del gráfico de respuesta amortiguada por fricción están representados por una línea recta que conecta todos los picos y otra línea recta que conecta todos los valles, con las dos líneas finalmente intersectando en el eje t. Los límites superior e inferior de la gráfica de respuesta viscosa subamortiguada están representados por una curva suave que conecta todos los picos y otra curva suave que conecta todos los valles, con ambas curvas acercándose pero nunca cruzando el eje t. — Figura\(\PageIndex{2}\): Respuesta del sistema en amortiguación por fricción y en amortiguación viscosa, para las mismas condiciones iniciales (\(x_0, \, v_0\)), constantes de resorte y masas.

Tenga en cuenta que la amortiguación viscosa tiene más reducción en amplitud antes (a pesar de la amortiguación relativamente ligera), pero continúa oscilando más allá del punto en que el sistema amortiguado por fricción se ha detenido (los valores relativos específicos dependen de los valores de constante de amortiguación y coeficientes de fricción). También tenga en cuenta que dado que el amortiguamiento viscoso es relativamente ligero, la diferencia de periodo entre las dos parcelas es bastante pequeña en este ejemplo.