Saltar al contenido principal
LibreTexts Español

15.4: Vibraciones Forzadas Armónicas No A

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    84058

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A menudo, los sistemas mecánicos no están experimentando vibraciones libres, sino que están sujetos a alguna fuerza aplicada que hace que el sistema vibre. En esta sección, consideraremos solo fuerzas armónicas (es decir, sinusoidales y cosenales), pero cualquier fuerza cambiante puede producir vibración.

    Cuando consideramos el diagrama de cuerpo libre del sistema, ahora tenemos una fuerza adicional para agregar: es decir, la excitación armónica externa.

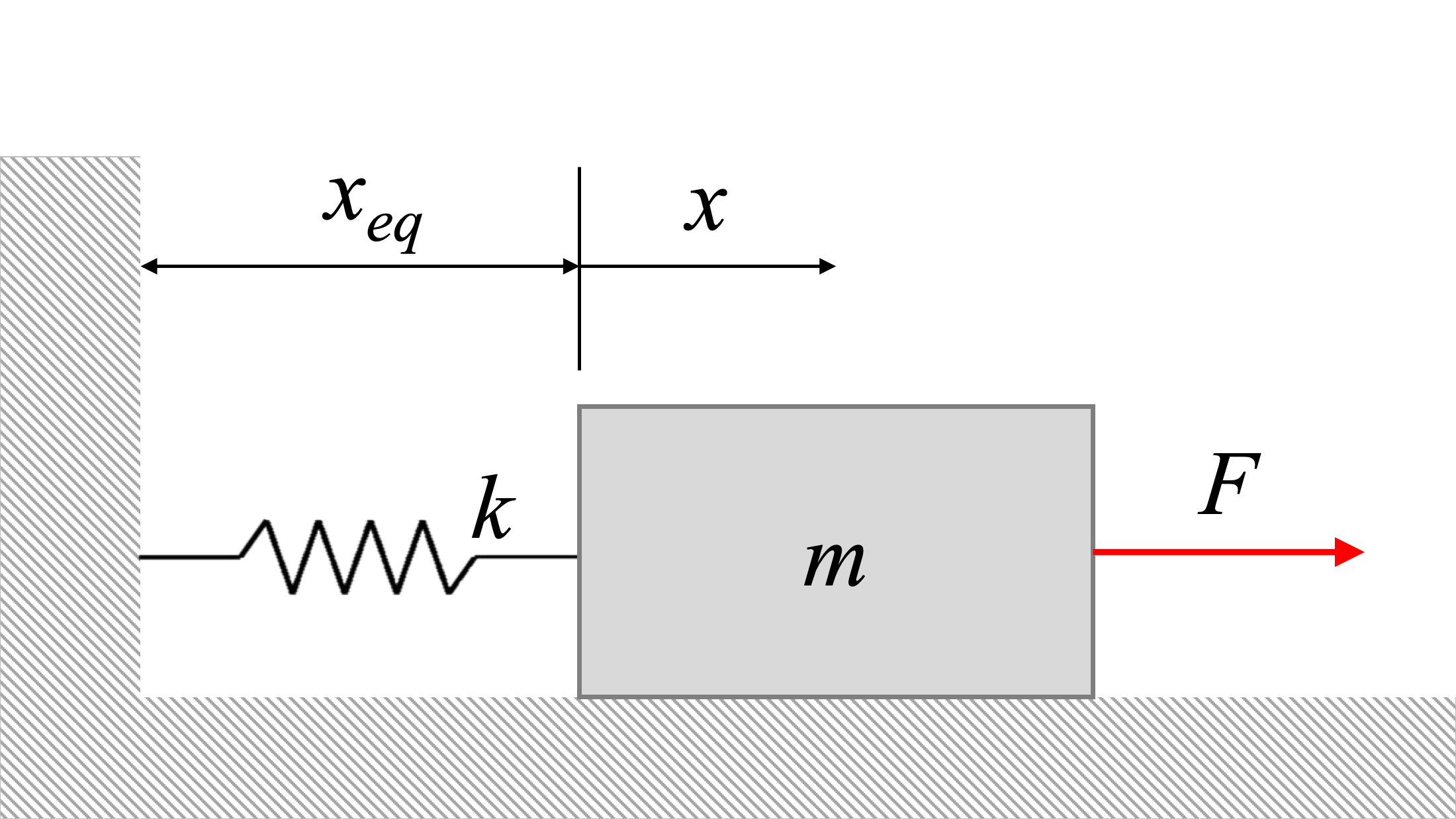
    Una masa rectangular se asienta sobre una superficie plana, con el extremo derecho de un resorte horizontal unido a su borde izquierdo. El extremo izquierdo del resorte está unido a una pared. El muelle está en su longitud no estirada x_eq, y la masa está en una posición x Se aplica una fuerza de tracción F al borde derecho de la masa, tirando de ella en la dirección x positiva.
    Figura\(\PageIndex{1}\): Un sistema masa-resorte con una fuerza externa\(F\), aplicando una excitación armónica.

    La ecuación de movimiento del sistema anterior será:

    \[ m \ddot{x} + kx = F, \]

    donde\(F\) es una fuerza de la forma:

    \[ F = F_0 \sin (\omega_0 t). \]

    Esta ecuación de movimiento para el sistema se puede reescribir en forma estándar:

    \[ \ddot{x} + \frac{k}{m} x = \frac{F_0}{m} \sin (\omega_0 t). \]

    La solución a este sistema consiste en la superposición de dos soluciones: una solución particular,\(x_p\) (relacionada con la función de forzamiento), y una solución complementaria,\(x_c\) (que es la solución al sistema sin forzar).

    Como vimos anteriormente, la solución complementaria es la solución al sistema libre sin amortiguar:\[x_c = C \sin (\omega_n t + \phi). \]

    Podemos obtener la solución particular asumiendo una solución de la forma:\[x_p = D \sin (\omega_0 t), \]

    donde\(\omega_0\) es la frecuencia de la función de forzamiento armónico. Diferenciamos esta forma de la solución, y luego subdividimos en la ecuación de movimiento anterior:

    \[ \ddot{x}_p = - \omega_0^2 D \sin (\omega_0 t) \]

    \[ - m \omega_0^2 D \sin (\omega_0 t) + k D \sin (\omega_0 t) = F_0 \sin (\omega_0 t) \]

    Después de resolver for\(D\), podemos usarlo para encontrar la solución particular,\(x_p\):

    \[ D = \frac{ \dfrac{F_0}{k}}{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \]

    \[ x_p = \frac{ \dfrac{F_0}{k}}{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \ \sin (\omega_0 t). \]

    Por lo tanto, la solución general para un sistema forzado y sin amortiguar es:

    \[ x_G (t) = \frac{ \dfrac{F_0}{k}}{1- \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \ \sin (\omega_0 t) + C \sin (\omega_n t + \phi) \]

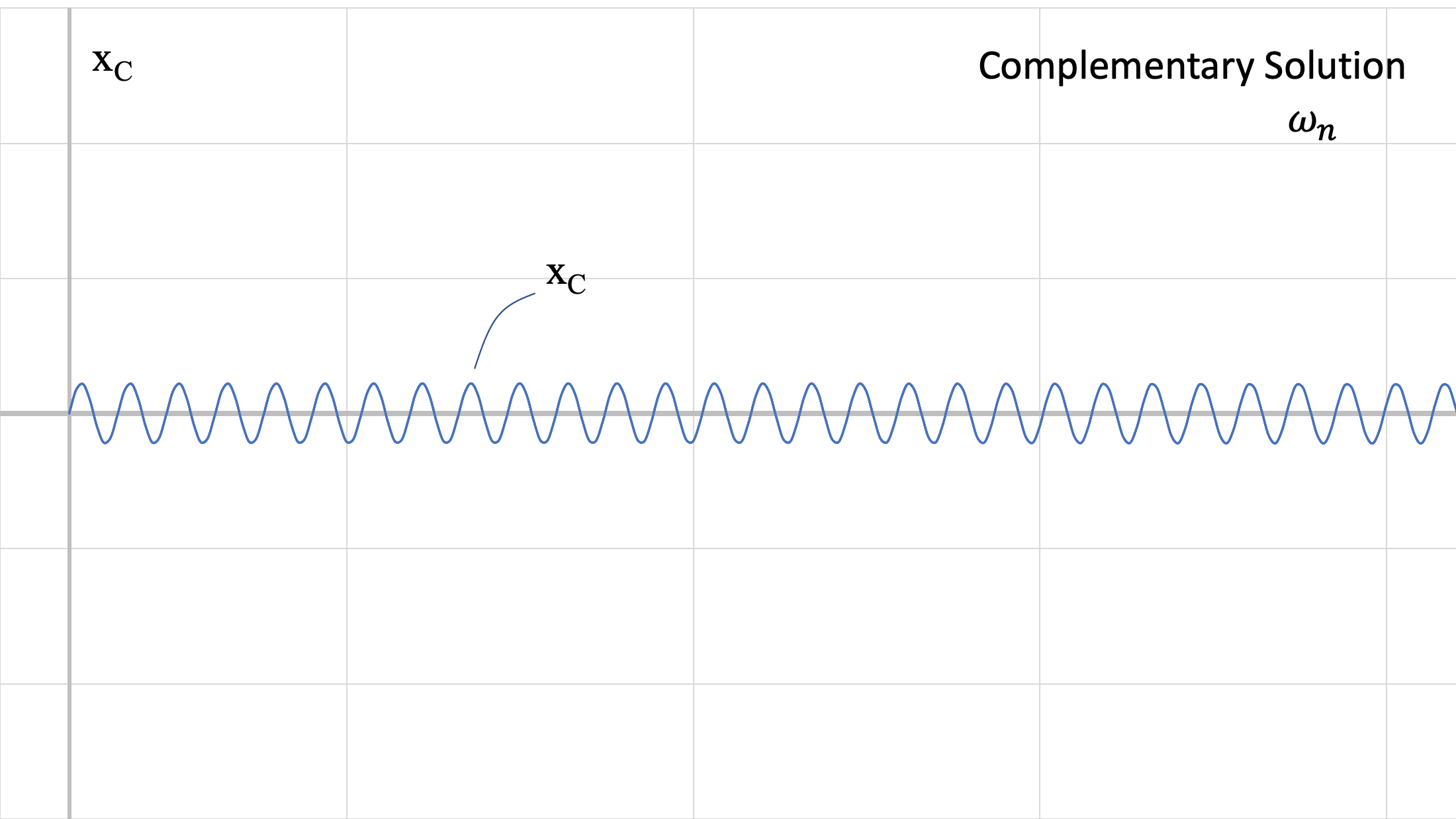
    Gráfica de la solución complementaria a la ecuación de movimiento del sistema, x_C, que toma la forma de una gráfica que oscila regularmente alrededor del eje t horizontal, siendo la amplitud y el periodo muy pequeños.
    Figura\(\PageIndex{2}\): La solución complementaria de la ecuación de movimiento. Esto representa la respuesta natural del sistema, y oscila a la frecuencia natural angular. Esta es la respuesta transitoria.
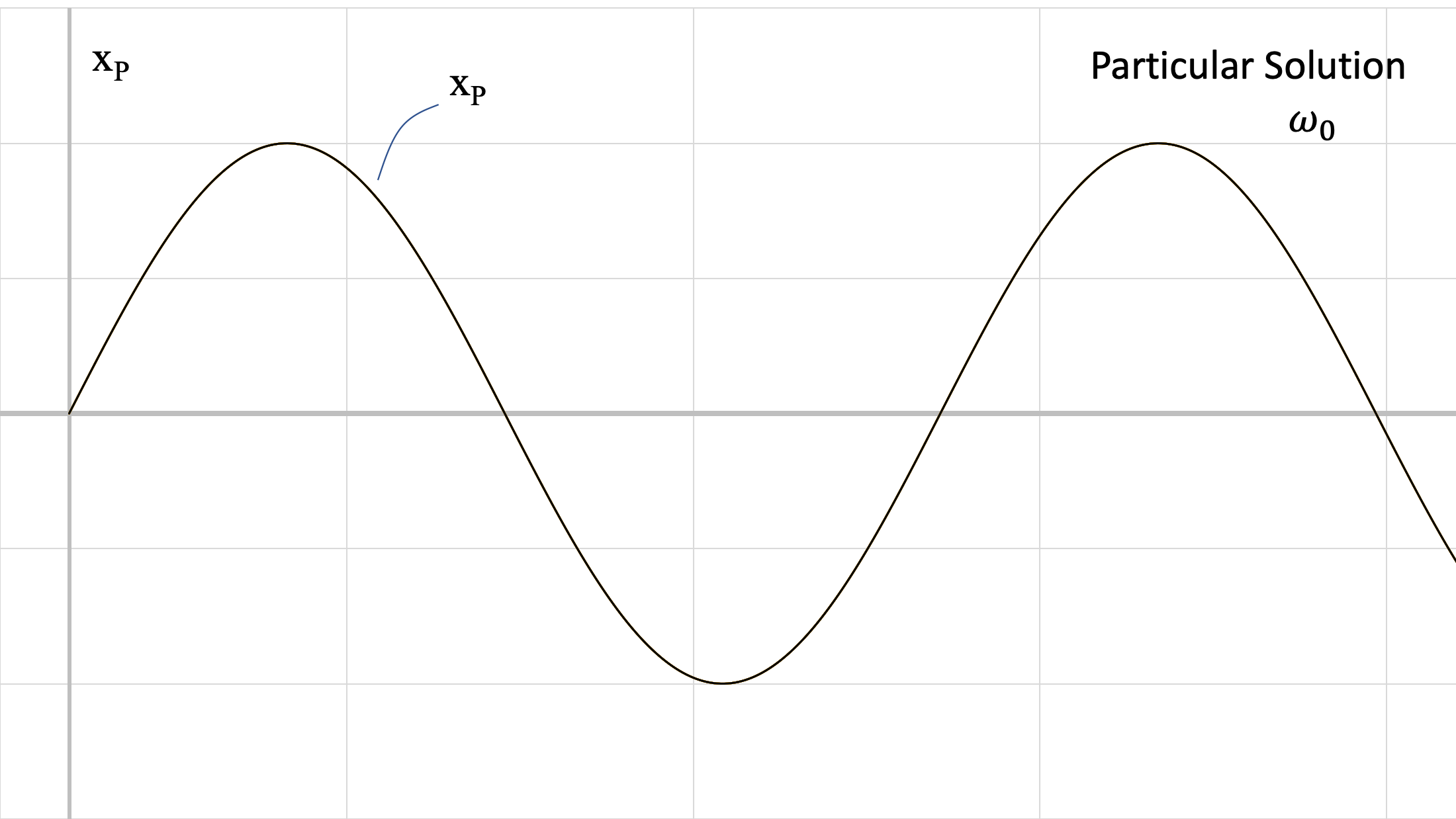
    Gráfica de la solución particular a la ecuación de movimiento del sistema, x_p, que toma la forma de una gráfica que oscila regularmente alrededor del eje t horizontal, siendo la amplitud y el período mucho mayores que los de la gráfica x_c.
    Figura\(\PageIndex{3}\): La solución particular de la ecuación de movimiento. Esto representa la respuesta forzada del sistema, y oscila a la frecuencia forzada angular. Esta es la respuesta en estado estacionario.
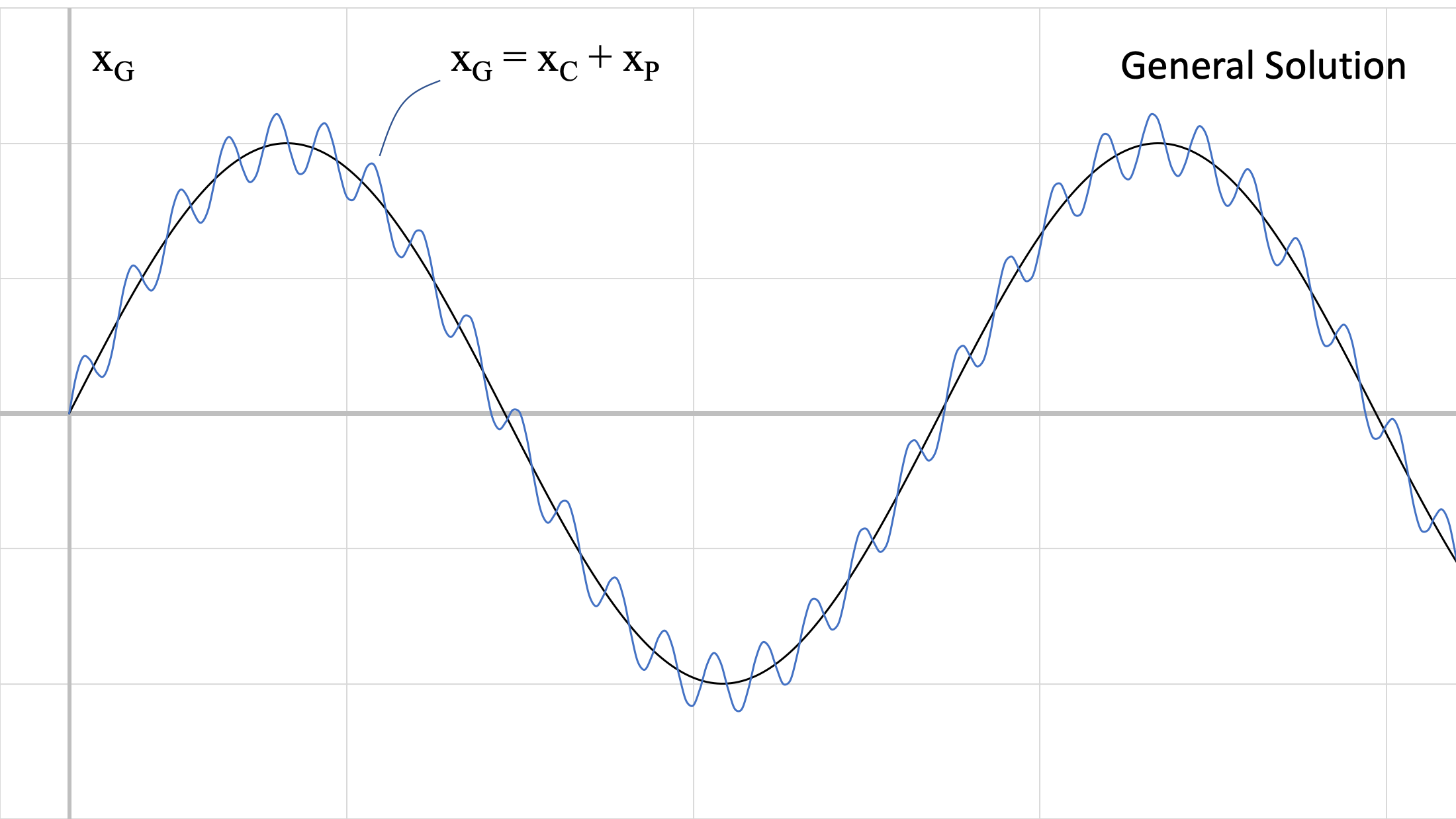
    Gráfica de la solución general a la ecuación de movimiento del sistema, x_g = x_c + x_p La forma general de esta gráfica sigue la de las grandes oscilaciones de x_p, pero mientras atraviesa esas grandes oscilaciones también pasa por oscilaciones menores e irregulares similares a las de x_c.
    Figura\(\PageIndex{4}\): La solución general de la ecuación de movimiento. Esto representa la respuesta combinada del sistema, y la suma de las respuestas complementarias (o naturales) y particulares (o forzadas).

    Las cifras anteriores muestran las dos respuestas a diferentes frecuencias. Recordemos que el valor de\(\omega_n\) proviene de las características físicas del sistema (\(m, \, k\)) y\(\omega_0\) proviene de la fuerza que se aplica al sistema. Estas respuestas se suman, para lograr la respuesta azul (solución general) en la Figura\(\PageIndex{4}\) anterior.

    Respuesta en estado estacionario:

    En realidad, esta respuesta superpuesta no dura mucho. Cada sistema real tiene alguna amortiguación, y la respuesta natural del sistema se amortiguará. Mientras se aplique la fuerza armónica externa, sin embargo, la respuesta a la misma permanecerá. Al evaluar la respuesta del sistema a una función de forzamiento armónico, normalmente consideraremos la respuesta de estado estacionario, cuando la respuesta natural se ha amortiguado y la respuesta a la función de forzamiento permanece.

    Amplitud de vibración forzada

    La amplitud de la vibración forzada en estado estacionario depende de la relación entre la frecuencia forzada y la frecuencia natural. A medida que\(\omega_0\) se acerca\(\omega_n\) (la relación se acerca a 1), la magnitud\(D\) se vuelve muy grande. Podemos definir un factor de aumento:

    \[ MF = \dfrac{ \dfrac{ \dfrac{F_0}{k}}{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2}} {\dfrac{F_0}{k}} = \dfrac{1}{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \]

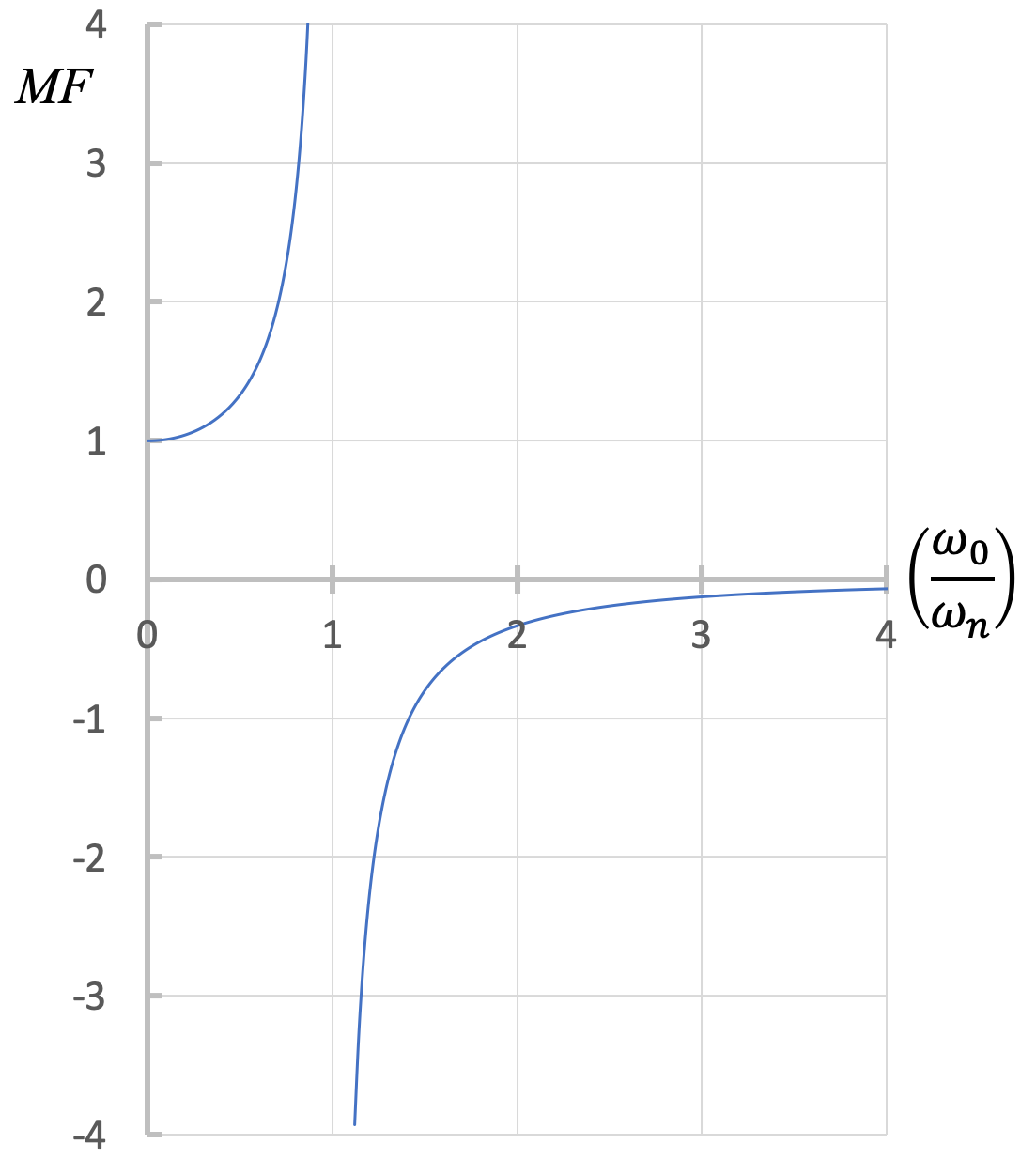
    Gráfica del factor de aumento MF, en el eje vertical, vs la relación entre la velocidad angular inicial y la frecuencia natural angular del sistema en el eje horizontal. La gráfica comienza en MF = 1 cuando la relación es 0, y va al infinito a medida que se acerca a la relación = 1 desde la izquierda. MF se acerca al infinito negativo a medida que la gráfica se acerca a la relación = 1 desde la derecha MF se acerca a 0 a medida que la relación va al infinito positivo.
    Figura\(\PageIndex{5}\): El factor de aumento,\(MF\), se define como la relación entre la amplitud de la vibración en estado estacionario y el desplazamiento que se lograría por deflexión estática.

    A partir de la figura anterior, podemos discutir diversos casos:

    • \(\bf{\omega_0 = \omega_n}\): Se produce resonancia. Esto da como resultado vibraciones de muy gran amplitud, y se asocia con altas tensiones y fallas en el sistema.
    • \(\bf{\omega_0 \sim 0, MF \sim 1}\): La función de forzamiento es casi estática, dejando esencialmente la desviación estática y la vibración natural limitada.
    • \(\bf{\omega_0 < \omega_n}\): La ampliación es positiva y mayor que 1, es decir, las vibraciones están en fase (cuando la fuerza actúa hacia la izquierda, el sistema se desplaza hacia la izquierda) y la amplitud de la vibración es mayor que la deflexión estática.
    • \(\bf{\omega_0 > \omega_n}\): La ampliación es negativa y el valor absoluto suele ser menor que 1, lo que significa que la vibración está desfasada con el movimiento de la función de forzamiento (cuando la fuerza actúa hacia la izquierda, el sistema se desplaza hacia la derecha) y la amplitud de la vibración es menor que la desviación estática.
    • \(\bf{\omega_0 >> \omega_n}\): La fuerza está cambiando de dirección demasiado rápido para que el movimiento del bloque responda.

    Desequilibrio giratorio:

    Una causa común de vibración forzada armónica en los sistemas mecánicos es el desequilibrio giratorio. Esto ocurre cuando el eje de rotación no pasa por el centro de masa, lo que significa que el centro de masa experimenta cierta aceleración en lugar de permanecer estacionario. Esto provoca una fuerza sobre el eje que cambia de dirección a medida que gira el centro de masa. Podemos representar esto como una pequeña masa,\(m\), girando alrededor del eje de rotación a cierta distancia, llamada excentricidad,\(e\). La frecuencia angular forzada\(\omega_0\), en este caso es la frecuencia angular del sistema giratorio.

    Ejemplo\(\PageIndex{1}\)

    Un ventilador de 10 kg se fija a una viga ligera. El peso estático del ventilador desvía la viga 20 mm. Si la cuchilla está diseñada para girar a\(\omega\) = 15 rad/s, y la cuchilla está montada descentrada (equivalente a una masa de 1.5 kg a 50 mm del eje de rotación), determine la amplitud de vibración en estado estacionario.

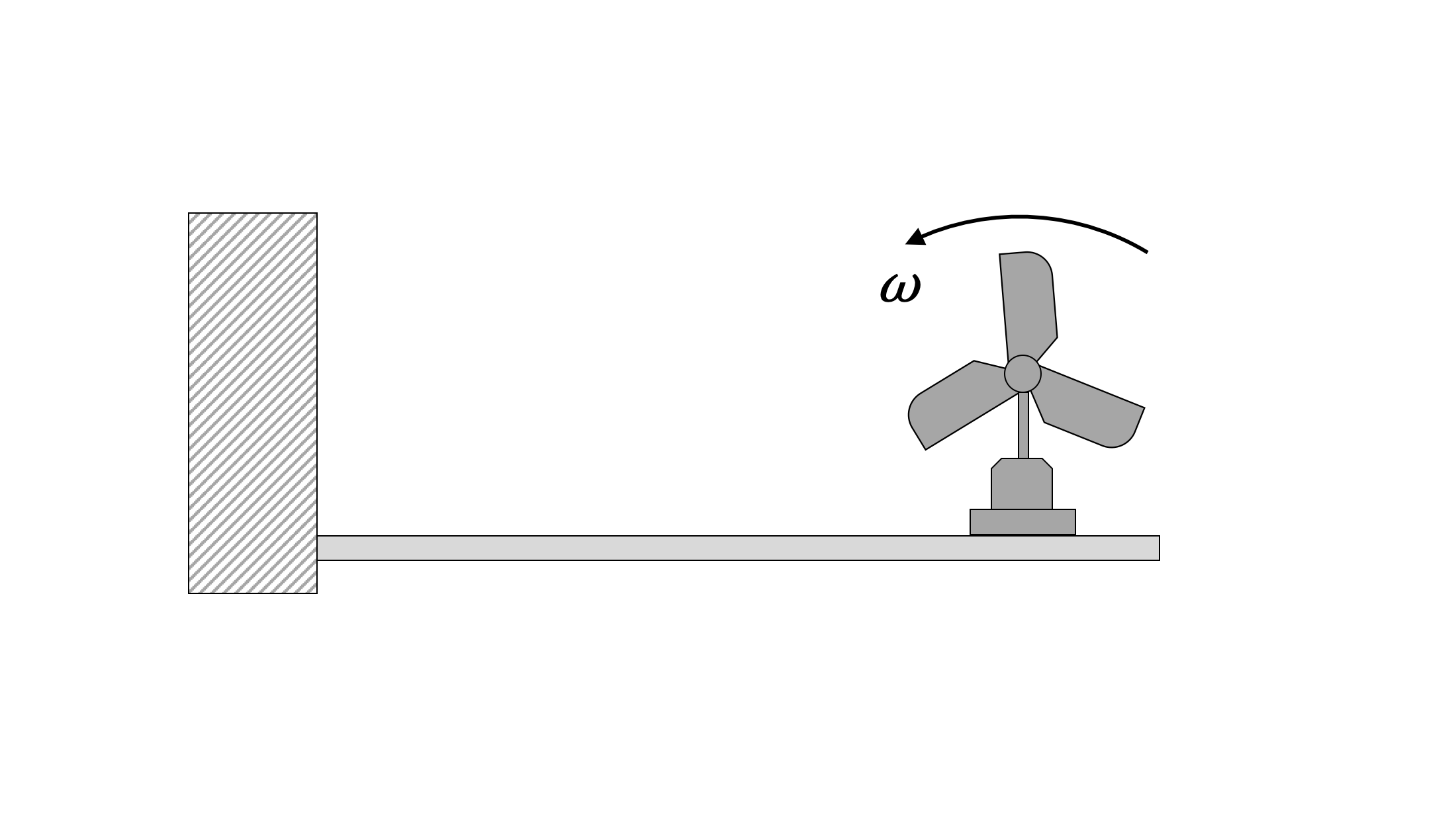
    Una viga horizontal que no está en contacto con el suelo se fija a una pared en su extremo izquierdo. La viga sostiene un ventilador de tres palas, que gira en sentido contrario a las agujas del reloj a velocidad angular omega, montado en un soporte en su extremo derecho.
    Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una viga horizontal que no toca el suelo está unida a una pared en su extremo izquierdo y sostiene un ventilador giratorio de tres palas en su extremo derecho.
    Solución:
    Video\(\PageIndex{1}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\). Fuente de YouTube: https://youtu.be/k0vJLxaAjtw.
    Ejemplo\(\PageIndex{2}\)

    Estás diseñando un ventilador elegante que usa solo una pala. Aproximar esa hoja como una placa estrecha con una densidad por unidad de longitud de 20 g/cm. El peso base del resto del dispositivo (a excepción de la cuchilla) es de 4 kg, y todo está montado en una viga liviana. Si la constante de resorte de la viga es\(k\) = 1000 N/m, encuentre la longitud de la pala que causará resonancia si el ventilador está diseñado para girar a\(\omega\) = 15 rad/s.

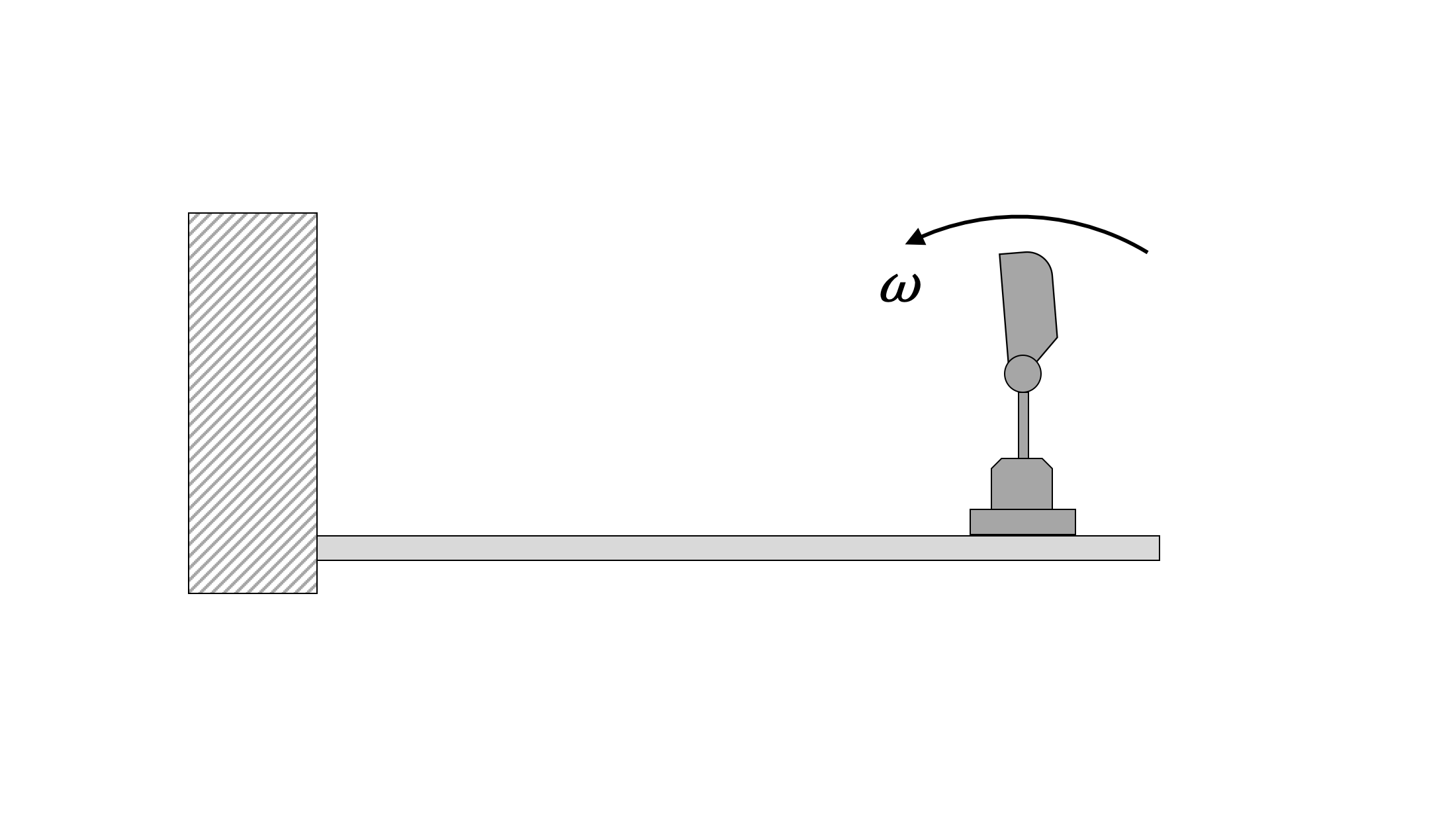
    Un ventilador consiste en una sola pala rectangular que se extiende desde un eje giratorio, que se monta sobre un soporte vertical unido a una base ancha. Este ventilador, que gira en sentido antihorario a una velocidad angular omega, está unido al extremo derecho de una viga horizontal. Esta viga se sostiene sobre el suelo por su extremo izquierdo estando fijado a una pared.
    Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Una viga horizontal que no toca el suelo está unida a una pared en su extremo izquierdo y sostiene un ventilador giratorio de una sola hoja a su derecha.
    Solución:
    Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\). Fuente de YouTube: https://youtu.be/tV4ETwwOyX0.

    This page titled 15.4: Vibraciones Forzadas Armónicas No A is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.