15.5: Vibraciones forzadas armónicas viscosas amortiguadas

Última actualización
Guardar como PDF

Page ID: 84047

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como se describe en la sección anterior, muchas vibraciones son causadas por una función externa de forzamiento armónico (como el desequilibrio giratorio). Si bien asumimos que las vibraciones naturales del sistema eventualmente se amortiguaron de alguna manera, dejando las vibraciones forzadas en estado estacionario, al incluir explícitamente la amortiguación viscosa en nuestro modelo podemos evaluar el sistema a través de la etapa transitoria cuando las vibraciones naturales están presentes.

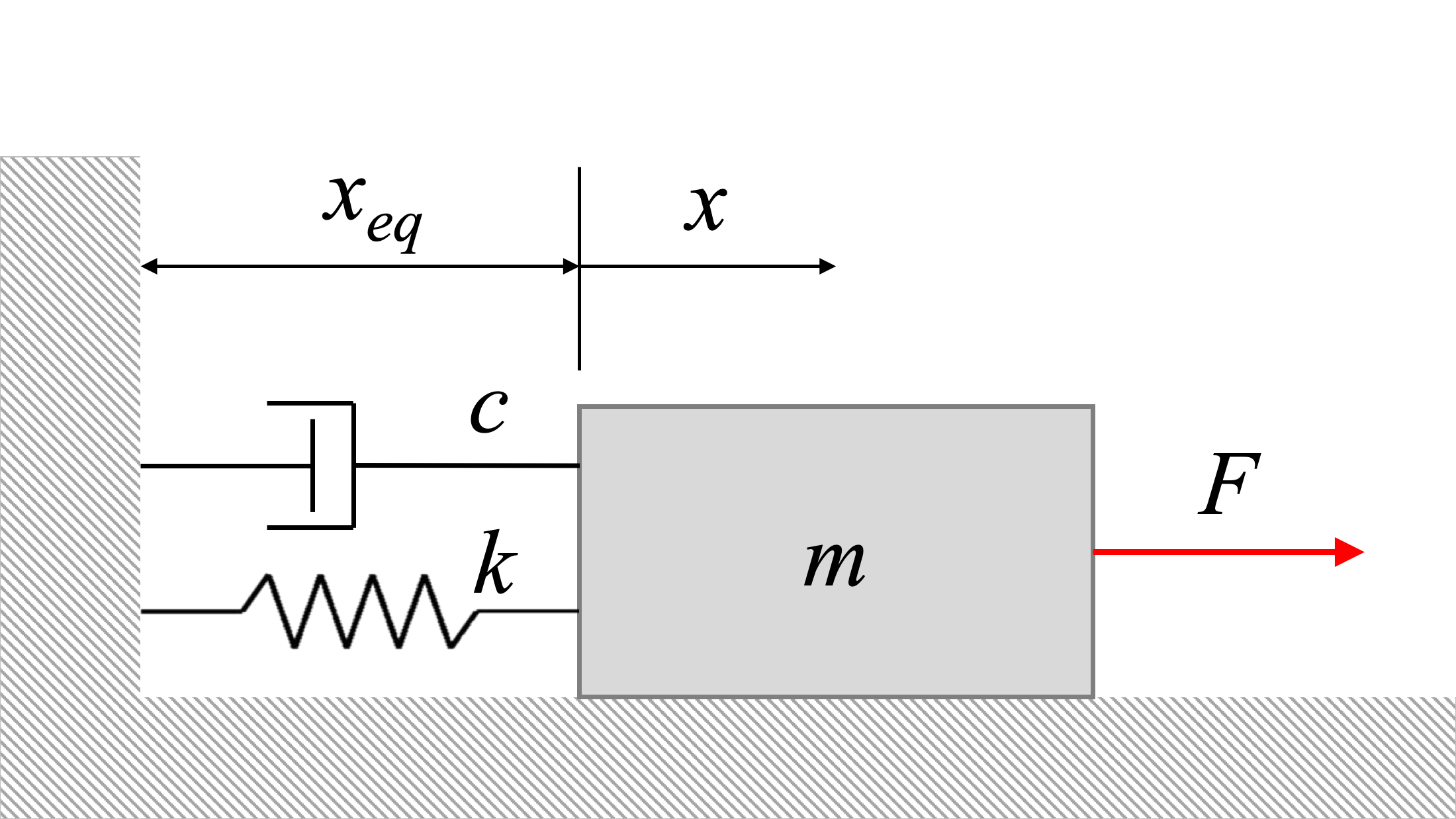
Se coloca una masa rectangular m sobre una superficie plana. Un resorte con constante de resorte k y un amortiguador lineal viscoso con constante de amortiguación c conectan el extremo izquierdo de la masa a una pared vertical. El resorte se encuentra actualmente en su longitud no estirada de x_eq. Se aplica una fuerza de tracción horizontal F al extremo derecho de la masa, moviéndola en la dirección x positiva. — Figura\(\PageIndex{1}\): Un sistema masa-muelle amortiguador con una fuerza externa\(F\), aplicando una excitación armónica.

Considera el sistema anterior. La ecuación del sistema se convierte en:

\[ m \ddot{x} + c \dot{x} + kx = F_0 \sin (\omega_0 t) \]

\[ \Rightarrow \ddot{x} + \frac{c}{m} \dot{x} + \frac{k}{m} x = \frac{F_0}{m} \ \sin (\omega_0 t). \]

Debido a que las vibraciones naturales se humedecerán con la fricción (como se menciona en las vibraciones armónicas no amortiguadas), solo consideraremos la solución particular. Esta solución particular tendrá la forma:

\[ x_p (t) = X' \sin (\omega_0 t - \phi '). \]

Después de resolver, determinamos que las expresiones para\(X'\) y\(\phi '\) son:

\[ X' = \frac{ \dfrac{F_0}{k}}{ \sqrt{ \left[ 1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2 \right] ^2 + \left[ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} \right] ^2 }} \]

\[ \phi ' = \tan ^{-1} \left[ \frac{ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} }{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \right]. \]

El factor de aumento ahora se convierte en:

\[ MF = \frac{X'}{\dfrac{F_0}{k}} = \dfrac{1}{\sqrt{ \left[ 1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2 \right] ^2 + \left[ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} \right] ^2 }} \]

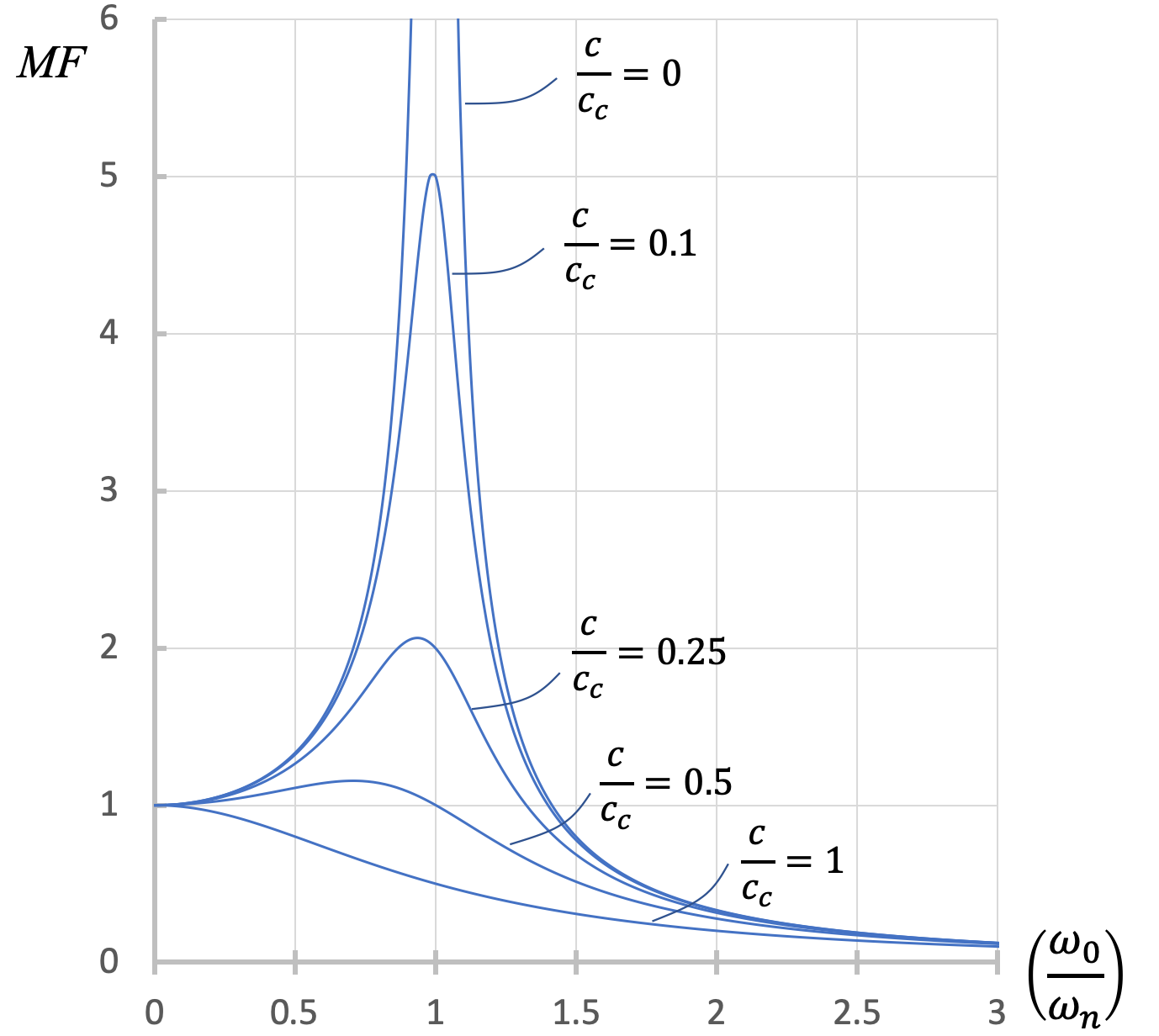
Gráfica de MF en el eje vertical vs la relación entre la velocidad angular inicial y la frecuencia natural angular del sistema en el eje horizontal, para valores variables de la relación de amortiguación. Cada gráfica comienza en el punto (0,1), alcanza una sola cresta cercana a x=1, y va a 0 a medida que el eje x va al infinito. La amplitud de esa cresta está en su mínimo cuando la relación de amortiguación es igual a 1, y va al infinito cuando la relación de amortiguación es igual a 0. — Figura\(\PageIndex{2}\): Esta figura muestra los diversos factores de aumento asociados a diferentes niveles de (bajo) amortiguamiento.

De la figura anterior, podemos ver que las amplitudes extremas en resonancia solo ocurren cuando la relación de amortiguamiento = 0 y la relación de frecuencias es 1. De lo contrario, la amortiguación inhibe las vibraciones fuera de control que de otro modo se verían en la resonancia.